
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розв’язування
Приклад виконання задачі 10
Бруса малої кривини при згині
Задача 10. Розрахунок на міцність та визначення переміщення
Завдання до розрахунково-графічної роботи
Для заданого кривого бруса (рис. 2.15) підібрати двотавровий переріз виходячи з умови міцності по нормальним напругам, якщо  МПа. Визначити кут повороту і горизонтальне переміщення перерізу в т. А. Радіус кривини вісі бруса 3 м, матеріал стержня – Ст. 3.
МПа. Визначити кут повороту і горизонтальне переміщення перерізу в т. А. Радіус кривини вісі бруса 3 м, матеріал стержня – Ст. 3.
План рішення
1. Побудувати епюри внутрішніх зусиль. Знайти небезпечний переріз.
2. Визначити розміри двотаврового перерізу із умови міцності по нормальним напругам, як для бруса малої кривизни, розташувавши переріз найвигіднішим чином.
3. Користуючись методом Мора, визначити горизонтальне переміщення і кут повороту в точці А без врахування осьової і поперечної сил.
Примітка. При виконанні завдання бажано виконати перевірку інтегрування, користуватись сучасними математичними прикладними пакетами програм (Mathcad, Mathlab, Mathematical тощо)
Таблиця 2.1
| № | Р1, кН | Р2, кН | М, кНм | α, ° |
Для заданого кривого бруса (рис. 2.16) підібрати двотавровий переріз, визначити кутове, горизонтальне та вертикальне переміщення перерізу в точці прикладення сили P2 . Матеріал стержня – сталь Ст. 3, допустимі нормальні напруження  МПа.
МПа.
Дано:
P1 = 5 кН; P2 = 10 кН;
М = 4 кН×м; R = 2 м,
a1 = p/2, a2 = 3p/2,  МПа
МПа
Знайти:
N(j), Q(j), М(j); № переріза; 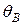 ,
, 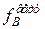 ,
, 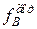 – ?
– ?
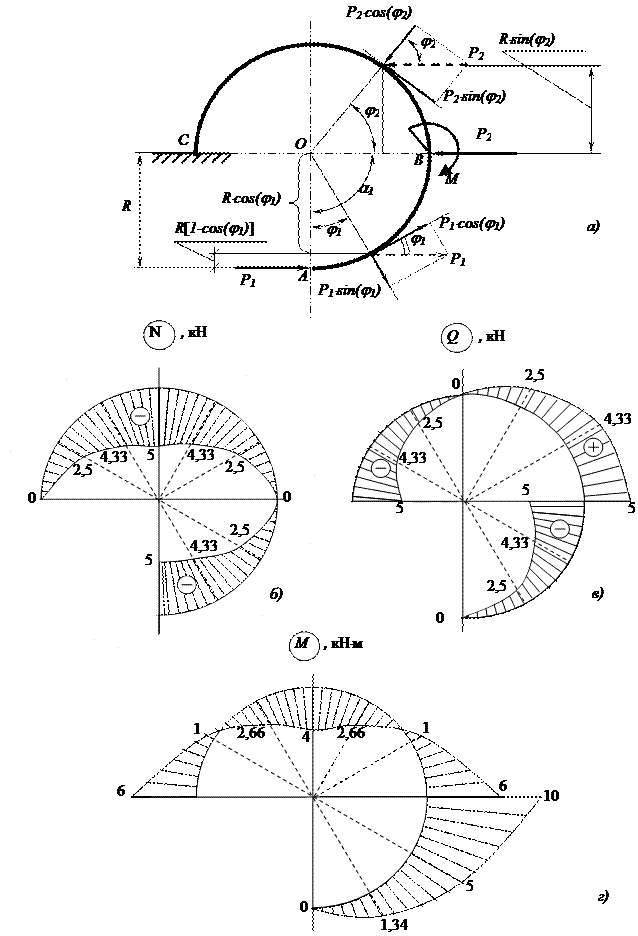
Будуємо епюри внутрішніх силових факторів*
Розділяємо стержень на дві ділянки і складаємо рівняння поздовжніх, поперечних сил та згинальних моментів для кожної з них (рис. 2.17).
* Методика побудови епюр для кривого стержня детально викладена, наприклад, в [1]
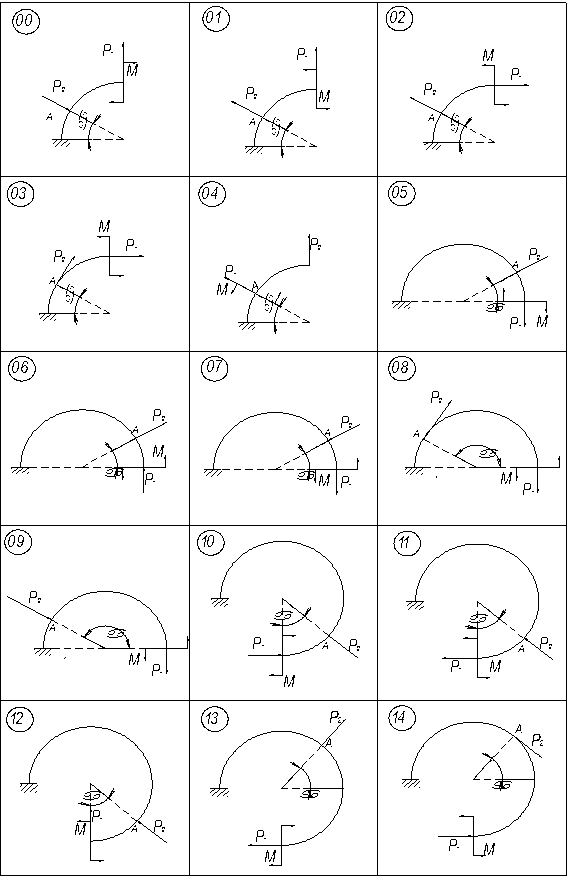
Рис. 2.15. Схеми до виконання задачі 10
 |
Ділянка АВ
0 £ j1 £ p/2.
N(j1) = –P1×cos(j1) = –5×cos(j1);
Q(j1 ) = –P1×sin(j1) = –5×sin(j1);
М(j1 ) = –P1×R×[1 – cos(j1)] = –10×[1 – cos(j1)].
Ділянка ВС
0 £ j2 £ p.
N(j2) = –P1×cos(j2 +a1) – P2×sin(j2) = –5cos(j2 + p/2) – 10sin(j2) = -5×sin(j2);
Q(j2 ) = –P1×sin(j2 +a1) + P2×cos(j2) = –5×sin(j2+p/2) +10×cos(j2) = 5×cos(j2);
М(j2 ) = –P1×R×[1 – cos(j2 + a1)] + P2×R×sin(j2) + М =
= –10×[1 – cos(j2)] + 20×sin(j2 – p/2) + 4 = -6 + 10×sin(j2).
З інтервалом в p/6 (300) знаходимо значення внутрішніх силових факторів в перерізах (таблиця 2.2).
Таблиця 2.2
| Ділянка АВ 0 £ j1 £ p/2 | Ділянка ВС 0£ j2 £ p | ||||||||||
| 00 | 300 | 600 | 900 | 00 | 300 | 600 | 900 | 1200 | 1500 | 1800 | |
| N(j) , кН | -5 | -4,33 | -2,5 | -2,5 | -4,33 | -5 | -4,33 | -2,5 | |||
| Q(j), кН | -2,5 | -4,33 | -5 | 4,33 | 2,5 | -2,5 | -4,33 | -5 | |||
| М(j), кН×м | -1,34 | -5 | -10 | -6 | -1 | 2,66 | 2,66 | -1 | -6 |
За отриманими значеннями будуємо на осі криволінійного стержня епюри поздовжніх N(j), поперечних сил Q(j) та згинальних моментів М(j) (рис. 2.17).
Ординати згинальних моментів відкладені в сторону стиснутих волокон без вказівки знаку. При прийнятому правилі знаків ординати зі знаком “+” до центра кривизни від осі стержня, “–” від центра кривизни від осі стержня. При побудові на розтягнутих волокнах – навпаки.
 | |||
|
1. Підбираємо переріз за умови міцності
Поперечними та поздовжніми силами нехтуємо. Також нехтуємо зміщенням нейтральної лінії від вісі стержня за рахунок малості його кривини.
Отже умова міцності
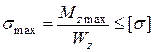 .
.
Необхідний момент опору
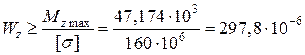 (м3) = 297,8 см3.
(м3) = 297,8 см3.
За сортаментом підбираємо двотавр №24а (додаток В), для якого  см3, Іz = 3800 см4.
см3, Іz = 3800 см4.
3. Визначаємо переміщення перерізу в т. А (кутове, горизонтальне, вертикальне та повне)
Згідно формули Мора для плоского стержня малої кривини
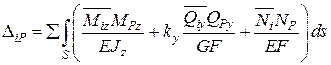
Нехтуємо переміщенням від дії поперечних та поздовжніх сил та переходимо до інтегрування по центральному куту j2 ( 0 £ j2 £ p)
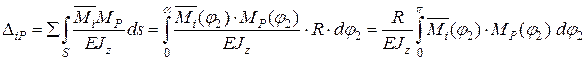 .
.
3.1 Кутове переміщення
Для визначення кутового переміщення прикладемо в т. В одиничний згинальний момент (рис. 2.18).
 (j2) = -6 + 10×sin(j2) .
(j2) = -6 + 10×sin(j2) .
Згинаючий момент в перерізі від цієї сили
 (j2) =
(j2) =  = 1.
= 1.
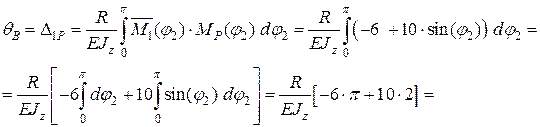
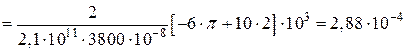 (рад) = 0,0170 .
(рад) = 0,0170 .
Значення інтегралів в виразі знаходили, використовуючи допоміжну таблицю додатка Д .
Знак “+” означає, що переріз повертається за напрямком одиничного момента  .
.
3.2 Вертикальне переміщення
Для визначення вертикального переміщення прикладемо в т. В вертикальну одиничну силу (рис. 2.19).

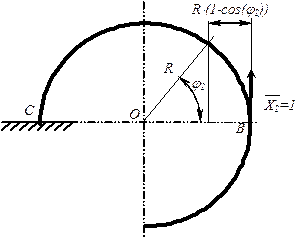
Рис. 2.18. Визначення кутового Рис. 2.19. Визначення вертикального
переміщення переміщення
Згинаючий момент в перерізі від цієї сили
 (j2) = -
(j2) = - ×R (1 – cos (j2)) = -1×2× (1 – cos (j2)) = -2 + 2 cos (j2).
×R (1 – cos (j2)) = -1×2× (1 – cos (j2)) = -2 + 2 cos (j2).
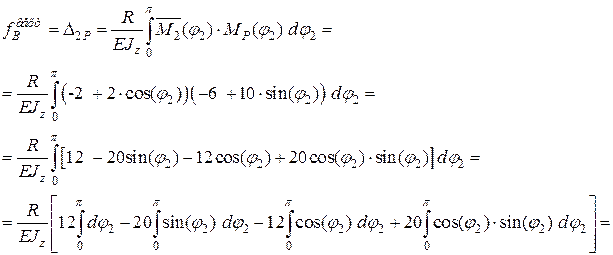
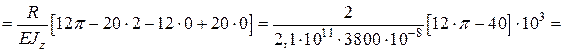
= -0,000577 (м) = -0,577 мм.
Знак “–” означає, що переріз переміщується проти напрямку одиничної сили 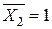 , тобто, вниз.
, тобто, вниз.
3.3 Горизонтальне переміщення
Для визначення горизонтального переміщення прикладемо в т. В горизонтальну одиничну силу.

Рис. 2.20. Визначення горизонтального переміщення
Згинаючий момент в перерізі від цієї сили
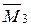 (j2) = -
(j2) = -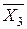 ×R×sin(j2) = -1×2× sin(j2) = -2 sin(j2).
×R×sin(j2) = -1×2× sin(j2) = -2 sin(j2).

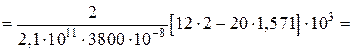 -0,00187 (м) = -1,87 мм.
-0,00187 (м) = -1,87 мм.
Знак “–” означає, що переріз переміщується проти напрямку одиничної сили 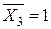 , тобто, ліворуч.
, тобто, ліворуч.
Повне переміщення знаходимо за теоремою Піфагора
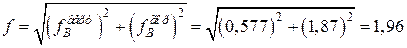 (мм).
(мм).
Відповідь: двотавр №14, 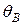 = 0,0170,
= 0,0170, 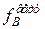 =0,577 мм,
=0,577 мм, 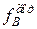 = 1,87 мм.
= 1,87 мм.
Питання до захисту розрахунково-графічної роботи (задача 10)
1. Які епюри будуються для розрахунку на міцність кривих плоских стержнів? Пояснити необхідність кожної епюри.
2. Записати інтеграл Мора при визначенні переміщень переріза кривого стержня та пояснити його.
3. За яким алгоритмом визначаються переміщення в стержневих системах довільної конфігурації?
4. Що називається вантажним станом?
5. Що називається одиничним станом?
6. Які відмінності розрахунку лінійного і кутового переміщення кривого стержня?
7. Що означає знак мінус перед числом визначеного переміщення?
8. Як визначити повне переміщення перерізу та його напрямок?
9. Визначити переміщення (кутове або лінійне) вказаного перерізу.
10. Чому при розрахунку переміщень стержневих конструкцій використовують лише залежності згинаючого моменту?
3. статично невизначувані системи (statically indeterminate system)
Читайте також:
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі оптимізації в Excel
- Графічний метод розв’язування задач лінійного програмування
- Завдання для самостійного розв’язування
- Загальна характеристика методів розв’язування цілочислових задач лінійного програмування
- Застосування перетворення за Лапласом для розв’язування диференціальних рівнянь
- Застосування рівнянь та їх систем до розв’язування текстових задач.
| <== попередня сторінка | | | наступна сторінка ==> |
| Обчислення інтегралів Мора способом Верещагіна | | | Короткі теоретичні відомості |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |