• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Короткі теоретичні відомості

3.1.1 Основні поняття та визначення

Як уже зазначалося, статично невизначуваними називаються системи, силові фактори в елементах яких тільки з рівнянь рівноваги визначити не можна. У таких системах зв'язків більше, ніж потрібно для рівноваги. Отже, деякі зв'язки виявляються в цьому розумінні так би мовити зайвими, а зусилля в них – зайвими невідомими. За числом зайвих зв'язків або зайвих невідо­мих зусиль установлюють ступінь статичної невизначуваності системи .

Розглянемо більш загальні випадки статично невизначуваних систем, причому основну увагу приділимо статично невизначуваним балкам та рамам.

На рис. 3.1, а зображено шарнірно обперту балку – систему статич­но визначувану і геометрично незмінювану. Всі три реакції (R_А, Н_А, R_В) визначаються з трьох умов рівноваги плоскої системи сил. Використову­ючи метод перерізів, легко знайти силові фактори Q, M будь-якому пе­рерізі балки.

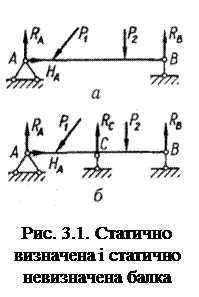Додамо ще один зв'язок, наприклад шарнірно-рухому опору в перерізі С (рис. 3.1,б). Хоч у наслідок цього система стала більш міцною та жорсткою, проте з погляду геометричної незмінюваності цей зв'язок зайвий. Тепер з трьох рівнянь рівноваги чотири реакції R_А, Н_А, R_В, R_С визначити не можна. Отже, зображена на рис. 3.1, б балка один раз статично невизначувана.

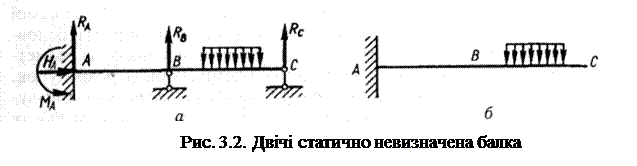
На рис. 3.2, а наведено двічі статично невизначувану балку. Для визна­чення п'яти реакцій є три рівняння рівноваги. Отже, система має два зайвих зв'язки. Вона може бути утворена, наприклад, із консолі (рис. 3.2, б) установленням шарнірно-рухомих опор у перерізах В та С.

У конструкціях часто застосовують статично невизначувані балки з ламаною віссю – рами. На відміну від ферм, де стрижні з'єднані між со­бою шарнірами й навантажені силами, прикладеними у вузлах, рами ма­ють один або кілька жорстких вузлів. У жорсткому вузлі торці з'єднува­них стрижнів не дістають відносних поступальних переміщень, а також відносних поворотів.

Рамні конструкції можуть складатись як з прямолінійних, так і з кри­волінійних елементів. На рис. 3.3 зображено двічі статично невизначува­ну плоску раму. В цьому прикладі, як і в попередньому, для визначення п'яти реакцій зовнішніх зв'язків маємо тільки три рівняння рівноваги.

Рами можуть бути навантажені цілком довільним навантаженням, будь-як орієнтованим.

Статична невизначуваність може бути наслід­ком не тільки введення додаткових зовнішніх зв'язків, а й умов утворення системи. Розглянемо раму на рис. 3.4, а. Очевидно, реакції R_А, Н_А, R_В зовнішніх зв'язків (опор) легко визначити з рівнянь рівноваги. Проте після цього рівняння рівноваги не дають змо­ги визначити всі силові фактори в елементах рами.

Розріжемо раму на дві частини й розглянемо рівно­вагу однієї з частин (рис. 3.4, б). Дію відкинутої частини на залишену замінимо в кожному з перерізів розрізу трьома силовими факторами: осьо­вою силою N,поперечною силою Q та згинальним моментом М.Отже, з трьох рівнянь рівноваги треба визначити дев'ять невідомих зусиль. Сис­тема шість разів статично невизначувана. Вона складається з двох замкне­них безшарнірних контурів, кожен з яких тричі статично невизначуваний.

Зазначимо, що встановлення шарніра на осі стрижня (рис. 3.5, а) пере­творює на нуль згинальний момент у даному перерізі й, отже, знижує сту­пінь статичної невизначуваності на одиницю. Такий шарнір називають одиночним. Очевидно, рама, зображена на рис. 3.5, а, п'ять разів статич­но невизначувана.

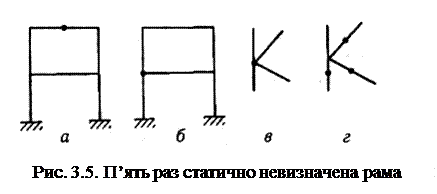
Шарнір, розміщений у вузлі, де збігаються п стрижнів (рис. 3.5, в), знижує ступінь статичної невизначуваності на п – 1, оскільки замінює собою таку саму кількість одиночних шарнірів (рис. 3.5, г). Такий шарнір називаєть­ся загальним. Рама, зображена на рис. 3.5, б,чотири рази статично невизна­чувана.

Ступінь статичної невизначуваності плоских систем можна виз­начати за формулою

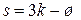, (3.1)

де s – ступінь статичної невизначуваності; k – кількість замкнених контурів за умови повної відсутності шарнірів; ш – кількість шарнірів у перерахунку на одиночні.

Основа (земля) розглядається як стрижень. Наприклад, рама, наведе­на на рис. 3.4, має чотири замкнених контури; біля кожного шарніра вказано відповідну кількість одиночних шарнірів, при цьому група стриж­нів, жорстко зв'язаних між собою, вважається одним стрижнем.

Тож у розглядуваному прикладі k = 4, ш = 1 + 2 + 1 + 1 + 1 = 6. Отже, s = 3∙4 – 6 = 6.

Для визначення зусиль у статично невизначуваних системах додатково до рівнянь статики складають так звані рівняння сумісності деформацій. Насправді, зайві зв'язки обмежують пе­реміщення тих перерізів, до яких вони прикладені. Цю обставину й вико­ристовують для складання додаткових рівнянь, які разом з рівняннями статики дають змогу визначити всі силові фактори в елементах системи.

Розглянемо етапи розрахунку статично невизначуваної системи.

1. Визначаємо ступінь статичної невизначуваності, тобто кількість зай­вих зв'язків або зайвих зусиль.

2. Усуваючи зайві зв'язки, заміняємо вихідну систему статично визначуваною, яку називають основною системою (main system). Вибір зайвих зв'язків залежить від бажання того, хто робить розрахунок. Тому для однієї й тієї самої статично невизначуваної вихідної системи можливі різні варіанти основ­них систем. Однак треба стежити за тим, щоб кожна з них була геометрично незмінюваною. Раціональний вибір системи спрощує розрахунок.

Отже, основною системою називається будь-який із статично визначу­ваних варіантів розглядуваної системи, здобутої звільненням її від зайвих зв'язків.

3. Завантажуємо основну систему заданим навантаженням і зайвими невідомими зусиллями, що заміняють дію усунених зв'язків. Така систе­ма називається еквівалентною системою (equivalent system).

3. Для того щоб основна система була еквівалентною вихідній системі, невідомі зусилля треба добирати так, щоб деформація основної системи не відрізнялася від деформації вихідної статично невизначуваної. Для цього прирівнюють до нуля переміщення точок прикладання невідомих зусиль у напрямі їх дії. Із добутих таким чином рівнянь знаходять значен­ня зайвих невідомих.

Визначати переміщення відповідних точок основної системи можна будь-яким способом, проте найкраще загальними методами – методом Мора або способом Верещагіна.

Знайшовши зайві невідомі зусилля, визначаємо реакції, будуємо епю­ри внутрішніх силових факторів, а також добираємо перерізи та перевіряє­мо міцність звичайними способами.

Наведена схема розрахунку має назву методу сил (work method), оскільки як основні невідомі тут вибирають зусилля зайвих зв'язків.

Читайте також:

1. IX. Відомості про військовий облік
2. IX. Відомості про військовий облік
3. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
4. Активне управління інвестиційним портфелем - теоретичні основи.
5. Білковий обмін: загальні відомості
6. Біографічні відомості
7. Боротьба з проявами національної самосвідомості
8. Вальниці ковзання. Загальні відомості
9. Види правосвідомості
10. Виникнення і розвиток свідомості у людини.
11. Виникнення людської свідомості. Мова і свідомість.
12. ВІДОМОСТІ ПРО ІНФОРМАЦІЮ, КІЛЬКІСНА МІРА ЇЇ. ВИДИ ПОВІДОМЛЕНЬ

Переглядів: 1082