• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розрахунок при осьовій дії ударного навантаження

Короткі теоретичні відомості

РОЗРАХУНКИ ПРИ УДАРНИХ НАВАНТАЖЕННЯХ (IMPACT LOAD)

Явище удару має місце тоді, коли швидкість розглядуваного елемента конструкції або стичних з ним частин протягом дуже малого проміжку часу змінюється на скінчену величину. Великі прискорення (сповільнен­ня), що виникають при цьому, приводять до появи значних сил інерції, які діють у напрямі, протилежному напряму прискорень, тобто в напрямі руху тіла. У випадку падаючого вантажу силу удару (динамічну силу Р_д) можна обчислити за формулою

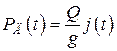, (5.1)

де Q – вага падаючого вантажу; g – прискорення вільного падіння; j(t) – прискорення падаючого вантажу після зіткнення його з перешко­дою.

Проте визначення сили удару Р_д(t) за формулою (5.1) пов'язане з великими труднощами, оскільки невідомий час співударяння, тобто час, протягом якого швидкість рухомого тіла зменшується від свого максимального значення в момент зіткнення з тілом, що ударяється (початок удару), до нуля після деформації останнього (кінець удару).

У зв'язку із зазначеними труднощами, що виникають при визначенні динамічних напружень та деформацій, в інженерній практиці виходять з так званої технічної теорії удару, яка ґрунтується на таких припущеннях.

1. При співударянні тіло, що ударяє, рухається разом з тілом, що зазнає удару, до розвитку найбільших деформацій. При цьому немає пружних хвиль у тілах і пов'язаних з ними відскоків тіла, що ударяє (такий удар
називають непружним).

2. За проміжок часу співударяння деформації поширюються по всьо­му об'єму тіла, що зазнає удару, а залежність між силами та деформація­ми, що виникають, відповідає закону Гука.

3. При співударянні рухомих тіл зменшення кінетичної енергії системи дорівнює збільшенню потенціальної енергії деформації тіл. При цьому нехтують втратами енергії на місцеві пластичні деформації, а також інер­цією маси тіла, що зазнає удару.

4. Вважають, що система тіл при співударянні має один степінь
вільності, тобто положення системи визначається однією координатою.

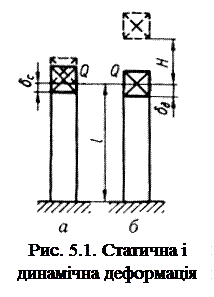
Формули для визначення динамічних напружень та деформацій при осьовому ударі наведемо на при­кладі системи (рис. 5.1), що складається з вертикально розміщеного пружного призматичного стрижня з жорст­кістю при розтяганні (стисканні) c = EF/l, на торець якого з висоти H вільно падає вантаж Q.

Припустимо, що вантаж прикладається до стрижня статично, тобто навантаження повільно наростає від нуля до максимального значення (рис. 5.1, а) і стискає стрижень на величину δ_с. При падінні вантажу з висо­ти H унаслідок удару на стрижень діятиме динамічна сила Р_д, більша ніж сила Q і укорочення стрижня δ_д буде більше за δ_с (рис. 5.1, б).

Зміна переміщень та деформацій при ударній дії навантаження Q по­рівняно з переміщеннями (деформаціями) при статичній дії того самого навантаження характеризується коефіцієнтом динамічності

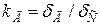, (5.2)

звідки динамічну деформацію через статичну можна виразити формулою

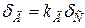. (5.3)

Ураховуючи лінійний зв'язок між напруженнями та деформаціями, а також припускаючи, що модулі пружності при статичній і ударній дії на­вантаження однакові, що з достатньою точністю підтверджується експе­риментом, можна за аналогією з формулою (5.3) встановити зв'язок між статичним та динамічним напруженнями:

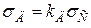, (5.4)

де

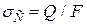(5.5)

– напруження, яке виникає в стрижні при стисканні силою, що дорівнює вазі падаючого вантажу.

Щоб використати формули (5.3), (5.4), треба визначити коефіцієнт динамічності k_д. Розраховуватимемо на підставі теорії удару, маючи на увазі, що залежність між силами та деформаціями має один і той самий вигляд як при статичних, так і при динамічних навантаженнях, тобто

; (5.6)

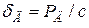, (5.7)

де р_с – статичне навантаження, що дорівнює вазі падаючого вантажу (у цьому разі Р_с = Q); р_д – динамічне навантаження, що є силою інерції тіла, яке ударяє, в перший момент його зіткнення зі стрижнем.

Коефіцієнт динамічності

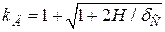. (5.8)

Маючи на увазі, що ( υ – швидкість падаючого вантажу в мо­мент початку удару), коефіцієнт динамічності можна записати у вигляді

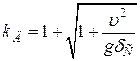. (5.9)

Тепер, виходячи із залежності (5.4), запишемо вираз для напружень при ударі:

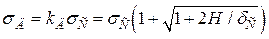, (5.10)

або

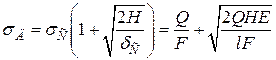. (5.11)

Аналогічно визначаємо зусилля при ударі:

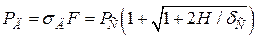. (5.12)

З аналізу формул (5.10) і (5.11) випли­ває, що при рівномірно розподілених напружен­нях, однакових в усіх поперечних перерізах стрижня, динамічні напруження залежать не тільки від площі F поперечного перерізу, як це має місце при дії статичного навантаження в статично визначуваних системах, а й від дов­жини l і модуля пружності Е матеріалу стрижня. Отже, можна сказати, що динамічні напруження в стрижні при ударі залежать як від об'єму, так і від якості матеріалу стрижнів. При цьому чим більший об'єм пружного стрижня, що зазнає удару (чим більша «енер­гоємність» стрижня), тим менші динамічні напруження, а чим більший модуль пружності матеріалу стрижня, тим динамічні напруження більші.

Сказане справедливе для призматичних стрижнів (стрижнів однако­вого поперечного перерізу).

Читайте також:

1. Автоматичний розрахунок суми проведення.
2. Агрегати для приготування, навантаження та внесення добрив.
3. Агрегати для приготування, навантаження та внесення добрив.
4. Аеродинамічний розрахунок
5. Аеродинамічний розрахунок ротора вітроустановки
6. Аналітичний розрахунок завантаження горловин
7. Аналітичний розрахунок сумарного завантаження типових перетинань
8. Важкість праці: Динамічні, статичні навантаження. Напруженість праці. Увага, напруженість аналізаторних функцій, емоційна та інтелектуальна напруженість, монотонність праці.
9. Варіанти навантаження ВТА і АА
10. Види норм праці, їх розрахунок
11. Визначення ударного тиску.
12. ВИЗНАЧЕННЯ ФІЗИЧНОГО ТА ЕМОЦІЙНОГО НАВАНТАЖЕННЯ НА ОРГАНІЗМ ПІДЛІТКІВ

Переглядів: 1882