
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклад виконання задачі 12
Задача 12. Проектний розрахунок на стійкість
Завдання до розрахунково-графічної роботи
Проектувальний розрахунок
У розрахунковій формулі на стійкість
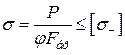 , або
, або 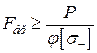 ,
,
є дві невідомі величини — коефіцієнт φ та шукана площа брутто Fбр поперечного перерізу. Тому при доборі перерізів слід користуватися методом послідовних наближень, варіюючи значення коефіцієнта φ. Як правило, в першій спробі беруть φ1 = 0,5 ... 0,4. Вибираючи будь-яке з цих значень φ1, визначають потрібну площу Fбр та добирають переріз. Вибраний переріз перевіряють та визначають фактичне значення  . Якщо
. Якщо  значно відрізняється від φ1 то й напруження відрізняється від допустимого. Тоді слід повторити розрахунок, тобто зробити другу спробу, взявши середнє за модулем значення між φ1 та
значно відрізняється від φ1 то й напруження відрізняється від допустимого. Тоді слід повторити розрахунок, тобто зробити другу спробу, взявши середнє за модулем значення між φ1 та  :
:
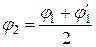 . (4.18)
. (4.18)
У результаті другої спроби визначають φ2. Якщо потрібна третя спроба, то
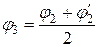
і т. д. Як правило, при доборі перерізів потрібно не більше ніж дві-три спроби.
Приклад. Доберемо за сортаментом двотавровий поперечний переріз стрижня завдовжки 5 м, що зазнає дії центрального стискального навантаження 320 кН. Обидва кінці стрижня затиснуті. Матеріал – Ст3. Основне допустиме напруження [σ–] =160 МПа.
Визначимо розрахункову зведену довжину стрижня:
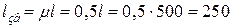 см.
см.
Добираємо поперечний переріз за методом послідовних наближень.
Перша спроба: вибираємо φ1 = 0,5; потрібна площа поперечного перерізу
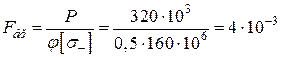 м2 = 40 см2.
м2 = 40 см2.
За сортаментом вибираємо двотавр № 27 з площею F = 40,2 см2 та мінімальним радіусом інерції iтіп = iст = 2,54 см. Гнучкість стрижня
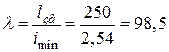 .
.
За табл. 4.2 при лінійній інтерполяції
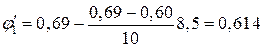 »φ1 = 0,4.
»φ1 = 0,4.
Перейдемо до другого наближення, взявши 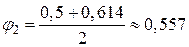 . Потрібна площа поперечного перерізу стрижня
. Потрібна площа поперечного перерізу стрижня
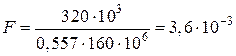 м2 = 36 см2.
м2 = 36 см2.
За сортаментом вибираємо двотавр № 24а з площею F = 37,5 см2 та мінімальним радіусом інерції iтіп = iст = 2,63 см. Гнучкість стрижня
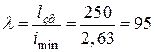 .
.
За таблиці Е.1 (додаток Е) знаходимо коефіцієнт  :
:
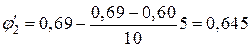 »φ2 = 0,557.
»φ2 = 0,557.
Переходимо до третього наближення, взявши
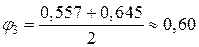 .
.
Обчислюємо потрібну площу:
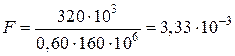 м2 = 33,3 см2.
м2 = 33,3 см2.
За сортаментом вибираємо двотавр № 24 з площею F = 34,8 см2 та мінімальним радіусом інерції iтіп = iст = 2,37 см. Гнучкість стрижня
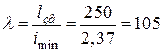 .
.
Для λ=105 коефіцієнт
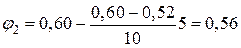 .
.
Обчислимо напруження:
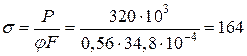 МПа.
МПа.
Перенапруження становить
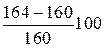 % ≈ 2,5%.
% ≈ 2,5%.
Остаточно вибираємо для стрижня двотавр № 24.
Стрижень завдовжки l складного поперечного перерізу зазнає дії центрального стискального навантаження Р (рис. 4.6). Матеріал – сталь Ст. 3, основне допустиме напруження [σ–] = 160 МПа.
Поперечний переріз стрижня прийняти згідно рис. 4.7. Схеми закріплення кінців стрижня в двох головних площинах подані в таблиці 4.1.
Необхідно:
- визначити раціональне розміщення перерізу щодо умов закріплення для подальшого розрахунок стояка на стійкість в площині мінімальної жорсткості;
- підібрати за сортаментом (додаток В) поперечний переріз стрижня, користуючись таблицями коефіцієнтів зниження допустимого напруження (додаток Е);
- обчислити критичну силу та запас по стійкості стрижня.
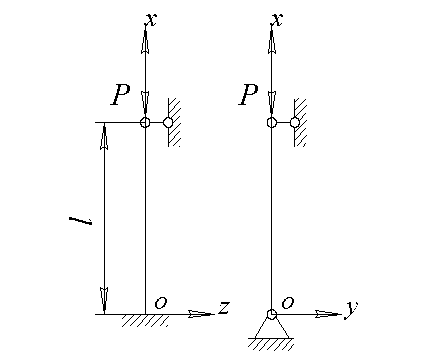
Увага! Умови закріплення приймати з таблиці 4.1
Рис. 4.6. Схеми закріплення кінців стержня
Таблиця 4.1
| № п/п | Р, кН | l, м | Спосіб закріплення кінців стояка | |||
| Площина XOZ | Площина XOY | |||||
| Нижній кінець | Верхній кінець | Нижній кінець | Верхній кінець | |||
| 8,5 | защемлення | шарнір | шарнір | шарнір | ||
| защемлення | шарнір | шарнір | шарнір | |||
| 7,5 | шарнір | защемлення | шарнір | шарнір | ||
| шарнір | шарнір | защемлення | защемлення | |||
| 6,5 | защемлення | защемлення | защемлення | шарнір | ||
| защемлення | шарнір | шарнір | шарнір | |||
| 5,5 | шарнір | шарнір | защемлення | шарнір | ||
| защемлення | вільне | шарнір | шарнір | |||
| 3,5 | шарнір | шарнір | защемлення | вільне | ||
| шарнір | шарнір | защемлення | шарнір |
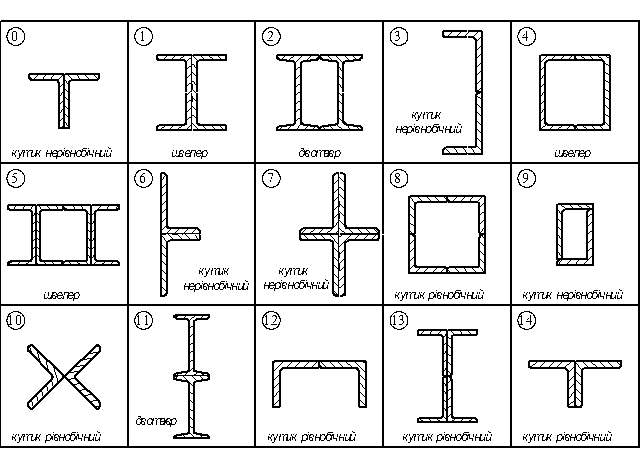 Рис. 4.7. Схеми до виконання задачі 12
Рис. 4.7. Схеми до виконання задачі 12
Стрижень завдовжки l = 6 м зазнає дії центрального стискального навантаження Р = 800 кН. Матеріал стержня – сталь Ст. 3. Основне допустиме напруження [σ–] =160 МПа. Підібрати за сортаментом поперечний переріз стрижня, що складається з двох жорстко з’єднаних між собою двотаврів (рис. 4.8, б).
Схеми закріплення кінців стрижня в двох головних площинах показані на рисунку (рис. 4.8, а). Розрахунок виконати для раціонального розміщення перерізу щодо закріплення. Обчислити запас по стійкості стрижня.
Розв’язування
Коефіцієнти умов закріплення стрижня згідно рис. Е.1 додатку Е
 .
.
1. Перша спроба
Задаємось φ1 = 0,5; потрібна площа поперечного перерізу (брутто)
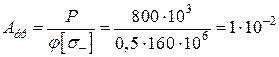 м2 = 100 см2.
м2 = 100 см2.
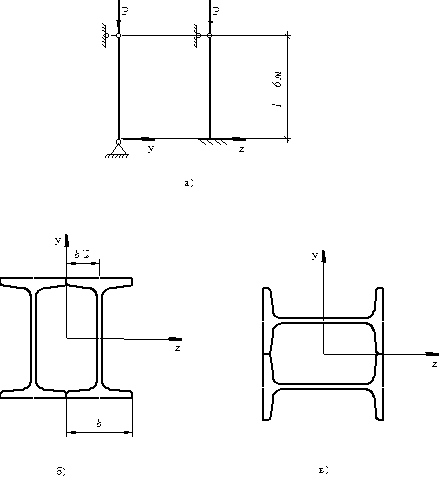
Рис. 4.8. Схеми до прикладу задачі 12
Потрібна площа одного двотавра
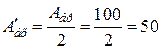 см2,
см2,
де 2 - кількість однакових двотаврів.
За сортаментом (додаток В) вибираємо двотавр №30а з такими геометричними характеристиками: площа А = 49,9 см2, радіус інерції iz = 12,5 см, ширина полиці 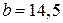 см, момент інерції
см, момент інерції 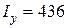 см4.
см4.
Вибираємо раціональне розміщення перерізу
Розміщуємо переріз так, як вказано на рис. 4.8, б.
Визначаємо радіус інерції відносно осі у
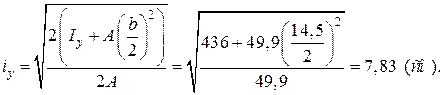
Гнучкість стрижня в двох головних площинах
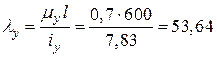 ;
;
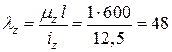 ;
;
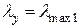 , отже розрахунок при такому виборі закріплення необхідно проводити по осі у (в площині хоz).
, отже розрахунок при такому виборі закріплення необхідно проводити по осі у (в площині хоz).
Розміщуємо переріз так, як вказано на рис. 4.8, в.
В такому випадку радіуси інерції iу = 12,5 см, iz = 7,83 см.
Гнучкості стрижня
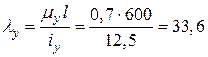 ;
;
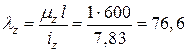 ;
;
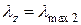 .
.
Оскільки 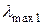 <
< 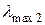 , то розміщення перерізу у випадку, показаному на рис. 4.8, б буде раціональним. Отже подальший розрахунок будемо проводити саме для такого закріплення.
, то розміщення перерізу у випадку, показаному на рис. 4.8, б буде раціональним. Отже подальший розрахунок будемо проводити саме для такого закріплення.
Вказівка. Раціональному розміщенню переріза завжди буде відповідати така умова: якщо 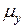 <
<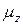 то
то 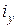 <
<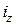 і якщо
і якщо 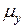 >
>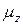 то
то 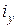 >
>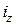 .
.
Таким чином, при 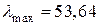 за табл. Е.1 (додаток Е) при лінійній інтерполяції
за табл. Е.1 (додаток Е) при лінійній інтерполяції
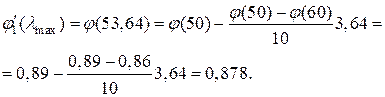
Оскільки 
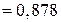 »φ1 = 0,5, то будемо проводити подальші уточнення. (Розв’язок вважається приблизно знайденим, якщо розбіжність між цими величинами складає не більше 5% від більшого значення)
»φ1 = 0,5, то будемо проводити подальші уточнення. (Розв’язок вважається приблизно знайденим, якщо розбіжність між цими величинами складає не більше 5% від більшого значення)
2. Друге наближення
Приймаємо
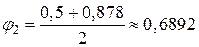 .
.
Потрібна площа поперечного перерізу
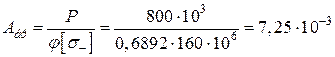 м2 = 72,5 см2.
м2 = 72,5 см2.
Потрібна площа одного двотавра
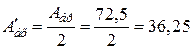 см2.
см2.
За сортаментом вибираємо двотавр №24а з такими геометричними характеристиками: площа А = 37,5 см2, радіус інерції iz = 10,1 см, ширина полиці 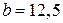 см, момент інерції
см, момент інерції 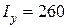 см4.
см4.
Визначаємо радіус інерції відносно осі у
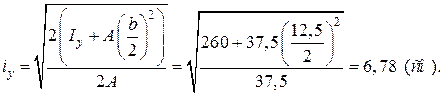
Гнучкість стрижня в двох головних площинах
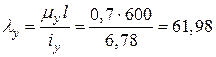 ;
;
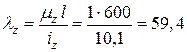 ;
;
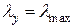 , отже розрахунок проводимо по осі у.
, отже розрахунок проводимо по осі у.
При 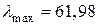 при лінійній інтерполяції
при лінійній інтерполяції
 .
.
Оскільки 
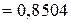 » φ2 =
» φ2 = 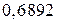 , то будемо в той самий спосіб проводити подальші уточнення.
, то будемо в той самий спосіб проводити подальші уточнення.
Для наочності подальші наближення, разом із попередніми зведемо в таблицю 4.2.
Таблиця 4.2
| № п/п | Величина | Наближення | |||
| перше | друге | третє | четверте | ||
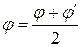
| 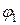 = 0,5 = 0,5
| 0,6892 | 0,7698 | 0,8034 | |
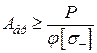 , см2 , см2
| 72,5 | 64,95 | 62,23 | ||
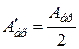 , см2 , см2
| 36,25 | 32,48 | 31,23 | ||
| Двотавр, номер | 30а | 24а | 22а | ||
| А, см2 | 49,9 | 37,5 | 32,8 | 30,6 | |
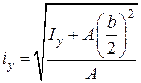 , см , см
| 7,83 | 6,78 | 6,502 | 5,948 | |
| iz , см | 12,5 | 10,1 | 9,22 | 9,13 | |
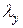
| 53,64 =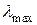
| 61,98
=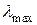
| 64,592 | 70,61=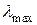
| |
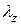
| 48,78 | 59,4 | 65,08
=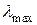
| 65,71 | |
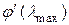
| 0,878 | 0,8504 | 0,837 | 0,8063 |
Вказівка.
Зверніть увагу на монотонне зростання або спадання розрахункових величин в таблиці в кожному рядку. Це ознака правильності проведення наближень. Якщо на черговому наближенні порушується така тенденція, то слід переглянути розрахунки саме на цьому етапі. Особливо це стосується перерізів, що складаються з кутиків, оскільки необхідній площі відповідають декілька кутиків з різними радіусами інерції. В цьому випадку необхідно прийняти інший розмір переріза та повторити наближення.
Бачимо, що в останньому наближенні 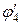
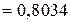 » φ4 =
» φ4 = 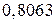 .
.
Обчислимо еквівалентні напруження:
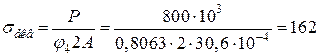 МПа.
МПа.
Перенапруження становить
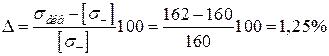 <
< 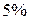 .
.
Допустиме значення перенапруження 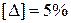 .
.
Вказівка.
Інколи два сусідніх за сортаментом переріза дають перенапруження і недонапруження, що перевищує допуск в 5%, тоді залишають переріз з недонапруженням, пояснивши вибір.
3. Визначаємо запас по стійкості
Оскільки 61 <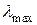 < 100, де 61 та 100 граничні значення гнучкості для сталі Ст. 3 (табл. Е.2, додаток Е), то критичне напруження визначаємо з формули Ясинського
< 100, де 61 та 100 граничні значення гнучкості для сталі Ст. 3 (табл. Е.2, додаток Е), то критичне напруження визначаємо з формули Ясинського
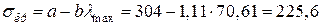 МПа.
МПа.
Критична сила
 (Н).
(Н).
Коефіцієнт запасу по стійкості
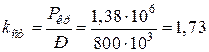 .
.
Відповідь: Двотавр №22, 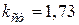 .
.
Питання до захисту розрахунково-графічної роботи (задача 12)
1. За яким алгоритмом підбирається переріз стиснутого стержня (із використанням коефіцієнта зниження допустимого напруження)?
2. Чому при проектному розрахунку використовують послідовні наближення?
3. Записати формулу Ейлера та пояснити її.
4. Записати формулу розрахунку гнучкості та пояснити її.
5. Записати умову стійкості стержня із використанням коефіцієнта зниження допустимого напруження та пояснити її.
6. В яких випадках критичні напруження розраховуються за формулою Ейлера (границі застосування формули Ейлера)?
7. В яких випадках критичні напруження розраховуються формулою Ясинського?
8. В яких випадках можна говорити про раціональне розміщення перерізу щодо умов закріплення? Якій умові відповідає це розміщення?
9. Чому при розрахунку на стійкість приймають до уваги лише максимальну гнучкість?
10. Що називається критичною силою?
11. Що таке запас по стійкості та як він визначається для заданого стержня і навантаження? Які орієнтовні значення запасу для різних конструкційних матеріалів?
Читайте також:
- III. Виконання бюджету
- III. Вимоги безпеки під час виконання роботи
- III. Вимоги безпеки під час виконання роботи
- V. Виконання вправ на застосування узагальнювальних правил.
- Абсолютні синоніми (наприклад, власне мовні й запозичені) в одному тексті ділового стилю вживати не рекомендується.
- Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
| <== попередня сторінка | | | наступна сторінка ==> |
| Перевірний розрахунок стиснутих стрижнів | | | Розрахунок при осьовій дії ударного навантаження |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |