• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Перевірний розрахунок стиснутих стрижнів

Розрахунки на стійкість за допомогою коефіцієнтів зменшення основного допустимого напруження

Можна вважати, що нейтрально стиснуті стрижні втрачають свою несучу здатність від втрати стійкості раніше, ніж від втрати міцності, оскіль­ки критичне напруження завжди менше за границю текучості або границю міцності:

σ_кр < σ_н,

де σ_н = σ_т – для пластичних матеріалів; σ_н = σ_в – для крихких матері­алів.

Слід нагадати, що для стрижнів малої гнучкості (λ < λ₀) важко казати про явище втрати стійкості прямолінійної форми стрижня, як це має місце для стрижнів середньої та великої гнучкості. Несівна здатність стрижнів малої гнучкості визначається міцністю матеріалу.

Критичне напруження для центрально стиснутих стрижнів середньої та великої гнучкості, мабуть, більш небезпечне, ніж границя текучості для пластичних матеріалів або границя міцності для крихких матеріалів при простому розтяганні. Очевидно, що при практичному вирішенні питання щодо стійкості стрижня не можна припустити виникнення в ньому кри­тичного напруження, а слід взяти відповідний запас стійкості.

Щоб визначити допустиме напруження на стійкість, треба вибрати коефіцієнт запасу п_ст. Тоді

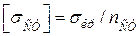. (4.13)

Коефіцієнт запасу на стійкість беруть дещо більший, ніж основний кое­фіцієнт запасу на міцність (п_ст > п ). Це обумовлено тим, що для центрально стиснутих стрижнів низка обставин, неминучих на практиці (ексцентриситет прикладання стискальних сил, початкова кривина і неоднорідність стрижня), сприяють поздовжньому згинанню, тоді як при інших видах деформації ці обставини майже не відбиваються. Коефіцієнт запасу стійкості для сталей вибирають у межах 1,8...3,0; для чавуну – 5,0...5,5; для деревини – 2,8...3,2. Зазначимо, що менші значення п_ствибирають для меншої гнучкості.

Допустиме напруження на стійкість 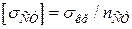та допустиме напруження на міцність при стисканні взаємно пов'язані. Складемо відношення їх:

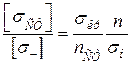, або 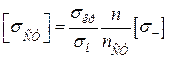. (4.14)

Позначивши

,

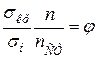матимемо

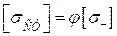. (4.15)

Тут φ – коефіцієнт зменшення основного допустимого напруження при розрахунку на стійкість. Цей коефіцієнт для кожного матеріалу мож­на обчислити при всіх значеннях гнучкості λ й подати у вигляді таблиці або графіка залежності φ від λ. Значення коефіцієнта φ для сталей, чаву­ну та деревини наведено в таблиці Е.1 (додаток Е). Користуючись аналогічними табли­цями, можна досить просто розрахувати стрижні на стійкість.

Таблиця 4.2

Складемо умову стійкості стиснутих стрижнів:

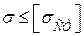. (4.16)

Оскільки

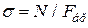, а ,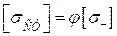

то умова стійкості набирає вигляду

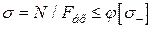. (4.17)

При розрахунку на стійкість місцеві ослаблення перерізу практично не змінюють значення критичної сили, тому в розрахункові формули вводиться повна площа F_бр поперечного перерізу.

Розглянемо два види розрахунку на стійкість стиснутих стрижнів – перевірний та проектувальний.

Порядок перевірного розрахунку на стійкість при використанні таблиці коефіцієнтів φ такий:

1) виходячи з відомих розмірів та форми поперечного перерізу, визначаємо найменший осьовий момент інерції J_min, площу F_бр, обчислюємо мінімальний радіус інерції

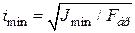
та гнучкість

;

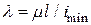2) за таблицею знаходимо коефіцієнт φ та обчислюємо допустиме на­пруження на стійкість за формулою

;

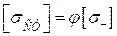3) порівнюємо дійсне напруження з допустимим напруженням σ_ст на стійкість:

.

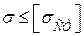Приклад. Перевіримо на стійкість стиснуту дерев'яну колону (рис. 4.5) квадратного поперечного перерізу (а =15 см) завдовжки l = 5м, якщо основне допустиме напруження [σ_–]=10 МПа, а стискальна сила Р = 100 кН.

Визначаємо такі величини:

площу –

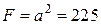см²;

момент інерції –

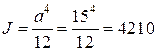см⁴;

радіус інерції –

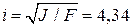см;

зведену довжину –

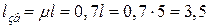м = 350 см;

гнучкість –

.

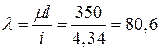За таблиці Е.1 (додаток Е) інтерполяцією знаходимо, що

.

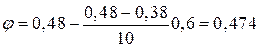Тоді

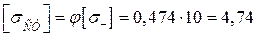МПа;

МПа.

Оскільки σ = 4,44 МПа < 4,74 МПа, то стійкість колони забезпечено.

Читайте також:

1. Автоматичний розрахунок суми проведення.
2. Аеродинамічний розрахунок
3. Аеродинамічний розрахунок ротора вітроустановки
4. Аналітичний розрахунок завантаження горловин
5. Аналітичний розрахунок сумарного завантаження типових перетинань
6. Види норм праці, їх розрахунок
7. Вплив характеру кола на криву струму при несинусоїдній напрузі /розрахунок найпростіших кіл
8. Гідравлічний розрахунок
9. Гідравлічний розрахунок малих мостів
10. Гідравлічний розрахунок сифонів
11. Графічний розрахунок режиму роботи ПСН
12. Графоаналітичний розрахунок витрат тепла і повітря на сушіння.

Переглядів: 942