• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Статично невизначувані задачі

Розрахунки на міцність за допустимими напруженнями

Допустиме напруження

Умови міцності вимагають, щоб напруження, які виникають в елементах конструкцій, не перевищували допустимих. Допустимі напруження [s] становлять деяку частину від небезпечних напружень. Для пластичних матеріалів таким небезпечним напруженням є границя текучості s_т , при якій деформації, що швидко зростають перешкоджають нормальній експлуатації конструкції. Для крихких матеріалів небезпечним напруженням є границя міцності s_в , при якій настає руйнування матеріалу. Допустиме напруження визначають за формулою

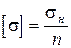(2.20)

де s_н = s_т - для пластичних матеріалів і s_н = s_в - для крихких, n - коефіцієнт запасу міцності при дії на конструкцію статичного навантаження встановлюється в межах n = 1,5...2, для крихких - n = 3...5, а іноді і вище (наприклад, для каменів природних і штучних він може бути в межах n = 10...30). Коефіцієнт запасу міцності залежить також від умов роботи конструкції, точності розрахунків напружень, характеру навантажень.

При розрахунках за допустимими напруженнями міцність конструкції або її елементів буде забезпечена, якщо максимальне напруження s_max не перевищує допустимого, тобто виконується умова

(2.21)

Формула (2.21) дає можливість розв’язувати такі інженерні задачі:

1. Підбір перерізу елемента конструкції при відомих силах, що діють на елемент (проектний розрахунок)

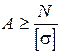(2.22)

2. Перевірний розрахунок, при якому визначають напруження і порівнюють його з допустимим

(2.23)

3. Визначення допустимого навантаження на існуючий елемент

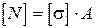(2.24)

Порядок виконання розрахунків.

1. Будують епюри нормальних сил і напружень (рисунок 2.1).

2. Задовольняють умову міцності (2.21) для перерізу, в якому має місце максимальне напруження. Якщо матеріал по різному чинить опір розтяганню і стисканню (характерно для крихких матеріалів), то найбільші розтягувальні напруження не повинні перевищувати допустимих напружень на розтягання [s]_р , а найбільші стискувальні напруження - допустимих напружень на стискання [s]_с .

Задачі на розрахунок конструкцій, в елементах яких силові фактори не можна визначити за допомогою лише рівнянь рівноваги статики, називають статично невизначуваними. При розв’язуванні таких задач, рівнянь яких не вистачає для визначення зусиль, складають на основі умов деформацій бруса або системи додаткові рівняння. Ці додаткові рівняння називають рівняннями сумісності деформацій (нерозривності деформацій). Від зв’язку між деформаціями, використовуючи закон Гука, переходять до рівнянь, які зв’язують зусилля в деформованих елементах. Рівняння сумісності деформацій мають різну форму, залежно від характеру задачі. Кількість таких задач визначає ступінь статичної невизначуваності задачі, який, очевидно дорівнює різниці між кількістю невідомих і кількістю рівнянь статики, які можна скласти.

Наведемо кілька прикладів.

Приклад 1.

Жорстка балка підтримується двома стержнями, як показано на рисунку 2.5. Перший стержень повинен мати площу поперечного перерізу в два рази більшу ніж другий; для матеріалу стержнів прийняти допустиме напруження [s]=1600 кг/см².Визначити площу поперечного перерізу стержнів.

Рисунок 2.5

. Дано: а=1 м; b=2 м; с=1,5 м a=45°; Р=120 кН; А1=2А2 Е1=Е2=Е; [s]=160 МПа Визначити: А1-?; А2-? Розв’язування: В задачі потрібно визначити площі перерізів стержнів, тобто провести проектний розрахунок. Оскільки стержні системи працюють на розтягання-стискання, то проектний розрахунок виконується за формулою

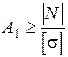
Допустиме напруження задано, тому потрібно визначити нормальні сили в поперечних перерізах стержнів 1 і 2.

Використаємо метод перерізів і переріжимо стержні поперечними перерізами, відкинемо верхню частину стержня 1 і нижню частину стержня 2, замінимо їх дію нормальними силами N₁ та N₂. Використовуючи формальний підхід, припустимо, що обидва стержні розтягнуті, тобто направимо N₁ та N₂ від перерізів. Відкинемо також шарнір і замінимо реакціями R_x та R_y (рисунок 2.6, а).

Для визначення чотирьох невідомих реакцій N₁ ,N₂ ,R_x ,R_y ми можемо скласти лише 3 незалежних рівняння статики, тобто

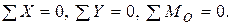
Отже, система 1 раз статично невизначувана.

Перші 2 рівняння статики крім N₁ та N₂ містять невідомі реакції R_x та R_y, визначати які немає необхідності. Отже, відносно невідомих зусиль N₁ та N₂ ми маємо лише одне рівняння:

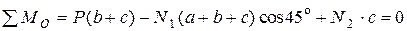(2.25)

Рисунок 2.6

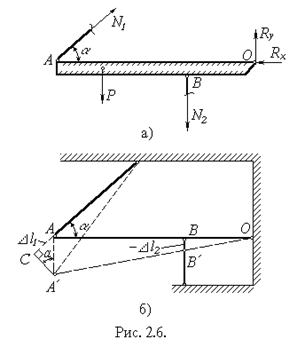
Для визначення N1 та N2 необхідно скласти рівняння сумісності переміщень. З цією метою розглянемо систему в деформованому стані. Методом засічок визначимо видовження Dl1. ІЗ подібності трикутників D ОВВ1 ¥ D ОАА1 випливає 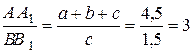АА1=3ВВ1 (2.26)   Із D АА1С АА1=Dl1/sin 45o На початку розв’язування задачі ми прийняли стержні розтягнуті, але за схемою

деформації другий стержень виявився стиснутим, таким чином відрізок ВВ₁ дорівнює Dl₂ із знаком мінус, тобто ВВ₁=-Dl₂.

З врахуванням цього отримаємо рівняння сумісності переміщень

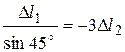(2.27)

Виразимо Dl₁ та Dl₂ через зусилля в стержнях N₁ та N₂

Враховуючи, що А₁=2А₂, підставимо вирази для

Dl₁ та Dl₂ в рівняння (2.27)

N₁= -3N₂ (2.28)

Сумісним розв’язуванням рівнянь (2.25) та (2.28) визначаємо N₁ та N₂

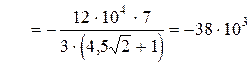Н

N₁=-3N₂=114×10³ Н

Отримані знаки зусиль говорять про те, що при навантаженні системи силою Р стержень 1 розтягується, а стержень 2 стискається. Порівняння величин N₁ та N₂ показує, що перший стержень більш навантажений. Визначаємо необхідну площу А₁

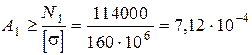м²=7,12 см²

Приймаємо А₁=7,2 см²

Тоді 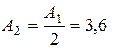см²

Перевіримо міцність 2-го стержня

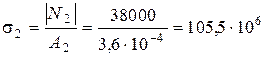Н/м² =105,5 МПа< [s]=160 МПа

Умова міцності виконується

Приклад 2.

Визначити зусилля в перерізах стержня (рисунок 2.7.).

Дано: Е_ст=2×10⁵ МПа; Е_м=1×10⁵ МПа ;

А_м=А_ст=А; Р=30 кН.

Рисунок 2.7

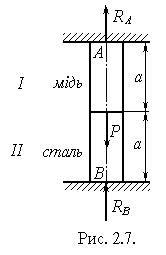
Розв’язування: Для визначення зусиль в поперечних перерізах використовують метод перерізів. Але для того, щоб використати цей метод нам необхідно визначити опорні реакції. Відкинемо опори і замінимо їх реакціями RA i RB . Сумістимо вісь z з віссю бруса. Для визначення невідомих RA i RB ми маємо лише одне рівняння статики   åZ=0 RA + RB - Р=0.   Дана задача відноситься до категорії статично

невизначуваних. При цьому ступінь статичної невиз начуваності дорівнює 1, тобто необхідно скласти одне рівняння сумісності переміщень.

З умови закріплення бруса очевидно, що переміщення крайніх перерізів А і В дорівнюють нулю (оскільки вони закріплені). Відкинемо нижнє закріплення, замінимо його дію реакцією R_B, значення якої поки що не відоме. Таким чином отримаємо статично визначуваний брус навантажений силами Р і R_B . Переміщення перерізу В визначається сумою деформацій 1-ї та 2-ї ділянок, тобто Але з умови закріплення d_з=0. Тоді рівняння сумісності переміщень має вигляд:

Dl₁ + Dl₂ = 0 (2.29)

Підставляючи в (2.29) отримаємо, з врахуванням того, що Е_ст=2Е_м

Звідси отримаємо Н

З рівняння (2.29) 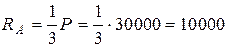Н

Методом перерізів визначаємо, що в перерізах 1-ї ділянки N₁=10 кН, а в перерізах 2-ї ділянки N₂=-20 кН.

Знаки зусиль показують, що перша, тобто мідна ділянка стержня - розтягнута, а друга (стальна) - стиснута.

Читайте також:

1. Алгоритм розв’язання задачі
2. Алгоритм розв’язання розподільної задачі
3. Алгоритм розв’язування задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі оптимізації в Excel
10. Аналіз інформації та постановка задачі дослідження
11. Багатопрольотні статично визначні балки
12. Взаємозв’язок характеристик порід, визначених при статичному і динамічному втискуванні

Переглядів: 1063