• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розрахунок температурних напружень в СНС

Особливістю статично невизначуваних систем (СНС) є виникнення в них температурних напружень. Температурними називаються напруження, які виникають в СНС при зміні температури всіх або окремих елементів системи.

Оскільки визначення температурних напружень є статично невизначуваною задачею, то доцільно їх розрахунки проводити за таким планом:

1. Записати незалежні рівняння статики.

2. Встановити ступінь статичної невизначуваності.

3. Скласти рівняння сумісності переміщень.

4. Замінити деформації через зусилля за законом Гука.

5. Розв’язати отриману систему рівнянь, визначити внутрішні зусилля.

6. Розрахувати напруження.

Приклад 3.

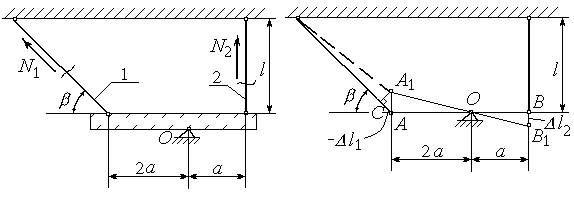
Жорсткий брус (рисунок 2.8), крім шарнірної опори, підтримується ще двома стальними тягами з площею поперечного перерізу А₁=40 см² та А₂=20 см². Після встановлення тяг їх температура підвищилась на Dt=+20^о. Визначити напруження в тягах.

Розв’язування:

Передбачити напрямок зусиль неможливо, тому припустимо, що система буде деформуватись таким чином, що обидва стержні будуть розтягнуті, тобто перший стержень буде після нагрівання розтягнутий зусиллям N₁, а другий розтягнутий зусиллям N₂. Уявно проводимо перерізи через два стержні і відділяємо брус від нижньої опори. В відповідності до принципу початкових розмірів рівняння статики можна складати для недеформованої системи. Для того щоб виключити реакції в шарнірній опорі в якості рівняння рівноваги візьмемо

(2.30)

Покажемо деформації окремих стрижнів. Тоді відрізок АС = -Dl₁, а ВВ₁ = Dl₂. Оскільки ми прийняли, що обидва стержні розтягнуті, то відрізок

АС дорівнює Dl₁ зі знаком ”мінус” оскільки за схемою деформації цей стержень стиснутий.

Із подібності трикутників ОАА₁ та ОВВ₁ маємо

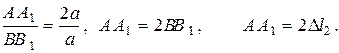(2.31)

Із прямокутного трикутника АСА₁ випливає

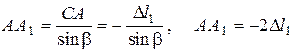(2.32)

Підставляючи (2.32) в (2.31) отримаємо

Dl₂=-Dl₁ (2.33)

Деформації Dl₁ та Dl₂ будуть викликані зусиллями N₁ та N₂ і підвищенням температури

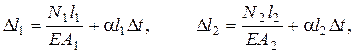(2.34)

де (2.35)

Підставляючи (2.34) в (2.33) з врахуванням (2.30) і (2.35) отримаєм

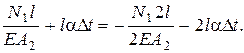
Після скорочень та перетворень отримаємо

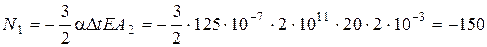кН

З умови (2.30) визначаємо

N₂=N₁=-150 кН.

Від’ємні знаки в N₁ і N₂ означають, що стержні 1 і 2 в дійсності не розтягнуті як ми прийняли, а стиснуті. Тоді напруження в стрижнях, викликані зміною температури

МПа

Мпа

При розв’язані задач, пов’язаних із визначенням температурних напружень в деяких випадках доводиться розв’язувати задачу з визначення граничної зміни температури Dt, при якій напруження в системі досягають граничної величини.

В такому випадку величину Dt визначають з умови

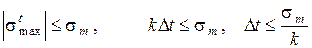
де k - числовий коефіцієнт, s_т - границя текучості матеріалу.

Читайте також:

1. Автоматичний розрахунок суми проведення.
2. Аеродинамічний розрахунок
3. Аеродинамічний розрахунок ротора вітроустановки
4. Аналітичний розрахунок завантаження горловин
5. Аналітичний розрахунок сумарного завантаження типових перетинань
6. Види норм праці, їх розрахунок
7. Визначення головнях напружень
8. Визначення допустимих напружень
9. Визначення нормальних напружень
10. Визначення нормальних напружень при згинанні
11. Вимірювання механічних напружень
12. Виникнення напружень та деформацій у зварних швах.

Переглядів: 656