• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Поняття про напружений стан

НАПРУЖЕНИЙ СТАН В ТОЧЦІ

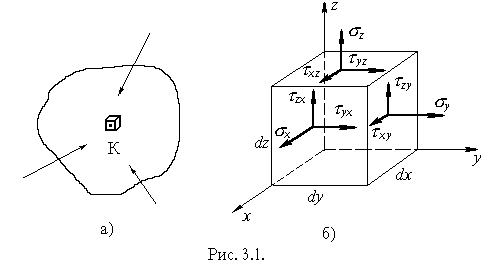
Розглянемо напруження в будь-якій точці К тіла, що деформується (рисунок 3.1, а). У розділі 1 зазначалося, що величина повного напруження, яке діє на довільній площадці, проведеній через точку К, залежить від орієнтації площадки. Напруження, які діють на незліченній кількості по-різному

Рисунок 3.1

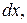
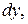
орієнтованих площадок, що проходять через розглядувану точку, характеризують напружений стан у точці. Метод вивчення напруженого стану в точці такий: вирізають елементарний паралелепіпед з ребрами (рисунок 3.1, б) і визначають напруження на його гранях. Враховуючи малість розмірів паралелепіпеда і те, що всі його грані є площадками, які проходять через точку К, то напруження по гранях паралелепіпеда можуть розглядатися як напруження, що діють у точці К.

Повні напруження, які діють на кожній грані, розкладаємо на три складові - на нормальне напруженняі дотичні , як показано на рисунку 3.1, б. На невидимих гранях елемента виникають відповідно такі самі за величиною, але протилежного напрямку напруження. Перший індекс у дотичного напруження вказує напрямок напруження, а другий - напрямок нормалі до площини перерізу. Нормальні напруження будемо позначати індексом осі, перпендикулярної до площадки.

Оскільки вирізаний елемент знаходиться в рівновазі, то склавши суму моментів усіх сил відносно осі х, маємо

,

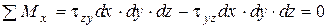звідки отримуємо . З рівнянь моментів відносно осей y і z маємо

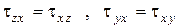(3.1)

Отже, у двох взаємно перпендикулярних площадках дотичні напруження перпендикулярні до спільного ребра і рівні за величиною. У цьому полягає закон парності дотичних напружень.

Таким чином, напружений стан в будь-якій точці напруженого тіла, яке деформується, визначається шістьма складовими s_x , s_y , s_z , t_{xy ,} t_xz, t_zy , які діють на трьох взаємно перпендикулярних площадках. Знаючи ці складові, можна знайти напруження в будь-якій площадці, проведеній через дану точку.

В курсі теорії пружності доводиться, що через незліченну кількість площадок, які можна провести через довільну точку напруженого тіла, завжди можна знайти такі три взаємно перпендикулярні площадки, на яких дотичні напруження дорівнюють нулю. Такі площадки називаються головними площадками, а діючі на них нормальні напруження - головними напруженнями. Головні напруження позначають s₁ , s₂ , s₃, при цьому повинна виконуватись умова s₁ > s₂ > s₃ (за алгебраїчною величиною).

Якщо в будь-якій точці навантаженого тіла усі три напруження відрізняються від нуля, то такий напружений стан називають об'ємним або триосним. Якщо з трьох головних напружень одне дорівнює нулю, то такий напружений стан називається плоским або двоосним. Напружений стан, при якому два головних (з трьох) напруження дорівнюють нулю, називається лінійним або одноосним. Прикладом лінійного напруженого стану є звичайний центральний розтяг (стиск) стержня.

Аналіз напруженого стану в точці необхідний в першу чергу для розрахунків на міцність в загальному випадку навантаження.

Напруження і деформації при лінійному напруженому стані розглянуті у розділі 2. Розглянемо напруження при плоскому напруженому стані.

Читайте також:

1. II. Поняття соціального процесу.
2. V. Поняття та ознаки (характеристики) злочинності
3. А/. Поняття про судовий процес.
4. Адміністративний проступок: поняття, ознаки, види.
5. Адміністративні провадження: поняття, класифікація, стадії
6. Акти застосування юридичних норм: поняття, ознаки, види.
7. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
8. АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ
9. Аудиторські докази: поняття та процедури отримання
10. Базове поняття земле оціночної діяльності.
11. Базові поняття
12. Базові поняття про класифікацію медичної техніки

Переглядів: 3255