• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Статичний момент площі. Центр ваги перерізу

ПЛОСКИХ ПЕРЕРІЗІВ

ГЕОМЕТРИЧНІ ХАРАКТЕРИСТИКИ

Практичні розрахунки на зріз і зминання

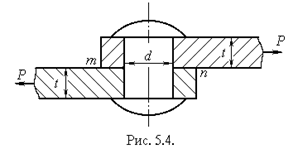
На практиці багато деталей конструкцій зазнають деформацій, близьких до деформації зсуву, і в таких випадках їх розміри визначають з розрахунку на зсув (зріз). Розглянемо, наприклад, роботу заклепки, що скріплює два стальних листи (рисунок 5.4).

Нехай на листи діють сили P, що намагаються зсунути їх один відносно одного. Цьому зміщенню перешкоджатиме стержень заклепки. На стержень заклепки передаються зусилля Р, які намагаються зрізати заклепку по площині mn.

Рисунок 5.4

Вважають, що дотичні напруження розподіляються по перерізу заклепки рівномірно (згином заклепки нехтуємо). Тоді їх величина

де 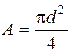- площа поперечного перерізу заклепки.

Позначимо через [t] допустиме напруження матеріалу заклепки на зріз. Тоді умова міцності матиме вигляд

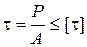(5.6)

При статичному навантажені звичайно беруть

,

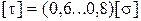де [s] - допустиме напруження на розтяг для того самого матеріалу.

Надійність з’єднання, показаного на рисунку 5.4, визначається не лишеміцністю заклепки проти перерізання. Тиск від листа на стержень заклепки передається по циліндричній поверхні. Цей тиск називається напруженням зминання s_зм . При надмірно високому значенні s_зм може відбутися зминання заклепки або листа. Внаслідок цього переріз заклепки або отвір у листі наберуть овальної форми. Для запобігання можливості зминання розрахунком встановлюють необхідну величину площі зминання А_зм . Умову міцності на зминання записують у вигляді

де [s]_зм - допустиме напруження зминання. Звичайно беруть

При контакті по циліндричній поверхні (рисунок 5.4) за розрахункову площу зминання умовно беруть площу проекції поверхні зминання на діаметральну площину. Для розглядуваного прикладу

Розглянемо, наприклад, розрахунок з’єднання стропильної ноги з стропильною затяжкою (рисунок 5.5).

Довжину частини затяжки визначимо з умови (5.6)

Рисунок 5.5

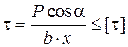звідси 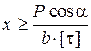  Необхідну площу зминання вирубки знайдемо з умови міцності (5.7)

звідси глибина вирубки .

Опір стержня різним видам деформації залежить не тільки від його матеріалу і площі поперечного перерізу, а і від форми поперечного перерізу, і його розміщення по відношенню до діючих навантажень. Досі вивчалися деформації, у яких напруження залежали тільки від площі поперечного перерізу. Для вивчення деформацій згину і кручення потрібно знати й інші, більш складні геометричні характеристики плоских перерізів

Статичним моментом S_z або S_y площі перерізу відносно осі z або y, які лежать у площині перерізу, називаються інтеграли виду

(6.1)

Рисунок 6.1

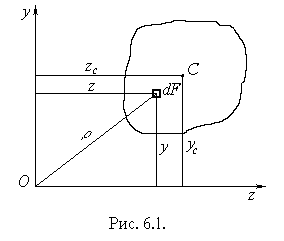
де z та y - відстані від центра елементарної площадки до осей Oz та Oy . У більшості практичних (інженерних) задач можна інтегрування замінити сумою, розділивши переріз на частини, площі і положення центрів ваги яких відомі, наприклад, переріз на рис. 6.2 можна розділити на окремі прямокутники. Тоді замість (6.1) можна записати

(6.2)

де n - кількість окремих частин перерізу,

А_i - площа частини перерізу,

z_i , y_i - відстані від центра ваги цієї площі до осей Oz та Oy.

Положення центра ваги перерізу C відносно будь-яких осей z та y (рисунки 6.1 і 6.2) визначається формулами

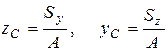, (6.3)

Рисунок 6.2

де А- площа перерізу, Sz та Sy - статичні моменти площі перерізу відносно осей z та y. Статичний момент площі може бути величиною додатною, від’ємною і дорівнювати нулю. Статичний момент відносно осі, яка проходить через центр ваги фігури (центральної осі) дорівнює нулю.

Читайте також:

1. IV. Система зв’язків всередині центральної нервової системи
2. А джерелами фінансування державні капітальні вкладення поділяються на централізовані та децентралізовані.
3. А. Центрогенна ДН
4. Аналіз витрат за центрами відповідальності.
5. Аналіз відхилень – основний інструмент оцінки діяльності центрів відповідальності
6. Аналіз відхилень — основний інструмент оцінки діяльності центрів відповідальності
7. Аналіз результатів практичної діяльності Київського освітньо-методичного центру соціальної роботи
8. Аналітичний вираз сил і моментів.
9. АНАТОМІЯ І ФІЗІОЛОГІЯ ЦЕНТРАЛЬНОЇ ТА ПЕРИФЕРИЧНОЇ НЕРВОВОЇ СИСТЕМИ, ЇЇ ВІКОВІ ОСОБЛИВОСТІ
10. Антиукраїнська політика російського царизму. Посилення централізаторсько-шовіністичних тенденцій
11. Арматура та вимірювальні прилади, якими обладнуються відцентрові насоси
12. Архіви центральних установ Великого князівства Литовського та Речі Посполитої. Литовська та Коронна метрики. Волинська метрика

Переглядів: 1375