Основи кореляційно-регресійного аналізу

У кореляційно-регресійному аналізі оцінка лінії peгpeciї здійснюється не в окремих точках, як в аналітичному групуванні, а в кожній точці інтервалу зміни факторної ознаки х. Тобто лінія peгpeciї у даному випадку безперервна i зображується у вигляді певно функції Y = f (х), яка називаєтъся рівнянням peгpeciї, а Y — це теоретичні значення результативної ознаки.

Різні явища по-різному реагують на зміну факторів. Для того, щоб відобразити характерні особливості зв'язку конкретних явищ, статистика використовує piзнi за функціональним видом регресійні рівняння. Якщо зі зміною фактора х результат змінюється більш-менш рівномірно, такий зв'язок описується лінійною функцією Y = а + bх, При нерівномірному співвідношенні варіацій взаємозв'язаних ознак (наприклад, коли прирости значень у зi зміною х прискорені чи сповільнені або напрям зв'язку змінюється), використовують нелінійні регресії, зокрема:

степеневу: Y = ах^b

гіперболу: Y = а +

параболу: Y = а + bх + сх²

Вибір та обгрунтування функціонального виду peгpeciї грунтується на теоретичному аналізі суті зв'язку. Припустимо, що вивчається зв'язок мiж урожайністю та кількістю опадів. Надто мала i надто велика кількість опадів спричиняють зниження урожайності, максимальний її рівень можливий за умови оптимальної кількості опадів, тобто зi збільшенням факторної ознаки (опади) урожайність спершу зростає, a потім зменшується. Залежність такого роду описується параболою Y = а + bх + сх².

Вивчаючи зв'язок між собівартістю у та обсягом продукції х, використовують рівняння гіперболи Y = а + b/х, де а — пропойні витрати на одиницю продукції, b — постійні витрати на весь випуск.

Слід зауважити, що теоретичний аналіз суті зв'язку, хоча і дуже важливий, лише окреслює особливості форми регресії i не може точно визначити її фунціональний вид. До того ж у конкретних умовах простору i часу межі варіації взаємопов'язаних ознак х i у значно вужчі за теоретично можливі якщо кривизна регресії невелика, то в межах фактичної варіації ознак зв'язок між ними досить точно описується лінійною функцією. Цим значною мірою пояснюється широке використання лінійних рівнянь регресії:

Y=a + bx

Параметр b (коефіцієнт регресії) — величина іменована, має розмірність результативної ознаки i розглядається як ефект впливу х на у. Параметр а — вільний член рівняння регресії, це значения у при х = 0. Якщо межі варіації x не містять нуля, то цей параметр має лише розрахункове значення.

Параметри рівняння регресії визначаються методом найменших квадратів, основна умова якого — мінімізація суми квадратів відхилень емпіричних значень у від теоретичних Y:

Σ(у-Y)²=mіn

Математично доведено, що значения параметрів а та b, при яких мінімізується сума квадратів відхилень, визначається із системи нормальних рівнянь.

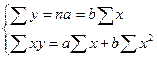
Розглянемо порядок обчислення параметрів лінійної peгpeciї за даними про вартість основних виробничих фондів та обсяг валової продукції на 10 підприємствах галузі (табл.10.7).

Таблиця 10.7 Показники діяльності підприємств

Hoмep підприємства Вартість основних виробничих фондів. млн.грн. Випуск валової продукції. млн.грн.

Передбачаючи лінійний зв'язок між вартістю основних виробничих фондів та випуском продукції, виражаємо залежність між цими показниками рівнянням прямої i визначаємо його параметри методом найменших квадратів із системи нормальних рівнянь:

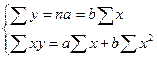
Розрахунки наведених в системІ рівнянь сум виконаємо в табличній формі (табл. 10.8):

Таблиця 10.8 Розрахункові показники

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Дисперсійний аналіз	\|	Для складання системи нормальних рівнянь

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.