• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Інтенсивного показника

Індекси динамики середнього рівня

У статистико-економічному аналізі нерідко доводиться порівнювати такі інтенсивні показники, як середня собівартість одинииці продукції певного виду, середня ціна, середня заробітна плата, середня урожайність однорідних культур тощо.

Аналіз динамики середнього рівня здійснюють на основі побудови системи взаємозалежних індексів. На середню величину впливає як значения ознаки х, яку осереднюють, так i чисельність окремих варіантів сукупності (частот). Очевидно, що й динаміка середньої величини визначаєтъся цими факторами: а) зміною значень ознаки х i б) структурними зрушеннями.

Відношення середніх рівнів інтенсивного показника за поточний i базисний періоди являє собою індекс змінного складу:

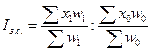або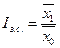

де х₁ і x₀ — piвні осередненого показника; w₁ і w₀ — частоти (ваги) інтенсивного показника.

Величина цього індексу залежить від двох факторів: зміни як самого осередненого показника, так i співвідношення частот, тобто структурних зрушень.

Визначити зміну середнього рівня інтенсивного показника за рахунок першого фактора дозволяє індекс фіксованого складу, а за рахунок другого — індекс структурних зрушень.

Формула індексу фіксованого складу має вигляд:

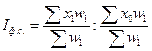або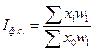

У цьому індексі структура сукупності фіксується на рівні звітного періоду, що i дає змогу проаналізувати зміну середньої лише за рахунок зміни рівнів інтенсивного показника.

Індекс структурних зрушень знаходять за формулою:

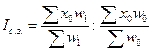
У цьому індексі фіксується на piвнi базисного періоду інтенсивний показник i, таким чином, визначається зміна середньої за рахунок структурних зрушень.

Miж індексами середніх величин icнyє такий взаємозв'язок:

І_з.с. = І_ф.с. * І_с.з.

У наведеній індексній системі індекс зміни середньої величини дорівнює добутку індексу при незмінній структурі на індекс, що відображує вплив зміни структури сукупності при незмінному значенні інтенсивного показника.

Обчислимо ці індекси i розглянемо їх економічний зміст на основі таких даних (табл. 9.3):

Таблиця 9.3. Обсяг виробннцтва виробу А

Читайте також:

1. Взаємозв'язок між показниками Балансу та Звіту про власний капітал
2. Взаємозв’язок облікових регістрів з показниками звітності.
3. Гігієнічне нормування умов праці за показниками важкості та напруженості праці
4. Еколого-економічна сутність показника декаплингу
5. За енергетичними показниками
6. За показниками віброакустичних факторів
7. За показниками мікроклімату
8. Класи умов праці за показниками важкості трудового процесу
9. Класи умов праці за показниками напруженості трудового процесу
10. Коефіцієнти подібності структур розподілу підприємств окремих галузей України за формами власності і взаємозв’язаними показниками за 1997—1998 роки
11. Коригування показника нерозподіленого прибутку на зміни в оборотних активах та поточних зобов'язаннях

Переглядів: 794