• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Закон розподілу швидкостей по перетину круглої труби при ламінарному режиму течії рідини.

Ламінарний рух рідини зустрічається досить рідко. У трубах ламінарний рух здійснюється в умовах перекачування в’язких мастил, мазуту та їм подібних рідин особливо при низьких температурах і невеликих швидкостях перекачування.

Ламінарна течія у круглій циліндричній трубі відбувається без поперечних переміщень частинок рідини, тобто паралельними шарами. В даному випадку можна уявити, що ці шари скручені у концентричні трубки, які рухаються поступально вздовж вісі труби, ковзаючи одна відносно другої, причому кожна така трубка повністю зберігає свою форму.

Вміння розраховувати видаток у ламінарному режимі, визначити втрати енергії, знати закон розподілу швидкостей і вміти виконати потрібні розрахунки – ось ті питання, які являють практичний інтерес для інженера-механіка.

Ламінарна течія внаслідок своєї простоти піддається теоретичному аналізу.

Теорія ламінарної течії рідини ґрунтується на законі тертя І. Ньютона. Це тертя між шарами рухомої рідини є джерелом втрат енергії у даному випадку.

Розглянемо сталу ламінарну течію рідини у круглій трубі (рис. 1) радіусом r. Щоб виключити вплив сили тяжіння і цим спростити вивід, припустимо, що труба розташована горизонтально. Виділимо в цьому потоці достатньо далеко від входу до неї, де потік вже стабілізувався, відрізок довжиною l між перетинами 1-1 і 2-2. Нехай у перетині 1-1 тиск буде дорівнювати p₁, а в перетині 2-2 – p₂ . З огляду постійності діаметру труби, швидкість рідини буде постійною, а коефіцієнт a буде незмінним вздовж потоку внаслідок його стабільності.

В цих умовах рівняння Д. Бернуллі для вибраних перетинів прийме вигляд:

.

Звідси 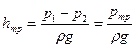, що і показують п’єзометри, які встановлені у вибраних перетинах.

Цей результат показує, що при рівномірній течії зменшення статичного напору дорівнює питомій енергії, яка витрачена на переборення сил тертя.

Виділимо у цьому потоці циліндричний об’єм рідини радіусом h і довжиною l. При русі цього циліндру на його боковій поверхні виникає сила внутрішнього тертя Т. Запишемо рівняння рівноваги рівномірного руху виділеного об’єму рідини у трубі відносно вісі потоку, враховуючи, що на об’єм рідини діє сила, яка викликає рух і сила опору.

Рис.1 Схема установки для дослідження ламінарного режиму

Рухомими силами у даному випадку є сили тиску, рівнодіюча яких визначається:

DР=(р₁ – р₂) p h²

Рівняння рівноваги:

DР=Т

Визначимо силу внутрішнього тертя Т:

T = –m ^. F,

де m - динамічний коефіцієнт в’язкості, m = rn;

F – бокова поверхня стискаємих шарів, F = 2phl.

Знак “–“ прийнято тому, що від’ємний (з ростом відстані від вісі потоку h швидкість частин рідини U зменшується).

Підставимо у загальне рівняння рівноваги значення сил:

,

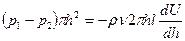або:

Поділимо останній вираз на rgl, після чого одержимо:

,

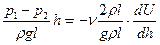або:

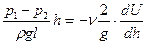
Якщо врахувати, що 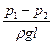є J – гідравлічний уклон, то

Градієнт швидкості з попереднього рівняння буде:

Розділимо змінні і отримаємо:

.

Після інтегрування:

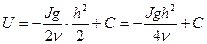
Постійну інтегрування С знайдемо з граничної умови: при h=r, U=0 (внаслідок прилипання рідини до стінок).

,

звідси:

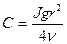
Підставляючи значення постійної С, одержимо:

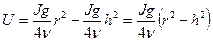
Таким чином, ми прийшли до висновку, що швидкість частин рідини пропорційна квадрату відстані її від вісі труби.

Цей вираз дає значення швидкості на будь-якій відстані h від вісі труби і відомий як закон Дж. Стокса.

Аналізуючи одержаний вираз, приходимо до висновку, що при ламінарному русі рідини ми маємо параболічний розподіл швидкостей.

Внаслідок цього епюра швидкостей при ламінарному русі (рис. 2) буде мати форму параболи.

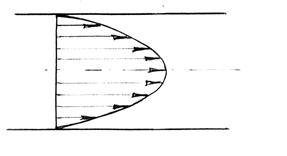
Рис. 2 Епюра швидкостей при ламінарному режиму руху рідини

При h=0,

Як відомо, величина дотичної напруги у потоці рідини визначається виразом:

В той же час і тоді:

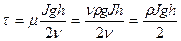
Із останнього виразу видно, що при ламінарному режимі руху рідини зміна t вздовж радіусу відбувається по лінійному закону, причому 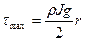буде при h=r, тобто біля стінки труби, а t_min=0, буде при h=0, тобто на вісі труби.

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
3. IV. Закони ідеальних газів.
4. IV. Закономірності структурно-функціональної організації спинного мозку
5. Авілум – “син чоловіка” – повноправна людина, охороні його життя, здоров’я, захисту його майнових інтересів присвячена значна частина законника.
6. Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
7. Автоматизація водорозподілу з комбінованим регулюванням
8. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
9. Автоматизація водорозподілу регулювання зі сталими перепадами
10. Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
11. Автоматизація водорозподілу регулюванням за верхнім б'єфом
12. Автоматизація водорозподілу регулюванням за нижнім б'єфом

Переглядів: 2377