• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Переведення чисел у неканонічну двійкову систему

з цифрами {1, }

Двійкова система з цифрами {1,} відрізняється від канонічної двійкової системи з цифрами {0, 1} тим, що серед використовуваних символів відсутній нуль. Ця обставина робить неможливим представлення в системі {1,} деяких цілих і дробових чисел у вигляді скінченої множини символів даної системи. Зокрема, неможливість представлення у вигляді скінченої множини цифр парних цілих чисел, наприклад 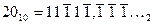приводить до використання нескінчених дробів, що зумовлює похибку при представленні цих чисел в системі {1,}.

В той же час існують числа, які не мають єдиного зображення, наприклад, число 1 може бути представлено у вигляді

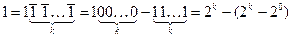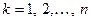, . (2.8)

Співвідношення (2.8) виражає зв’язок між канонічною двійковою системою і системою {1,}.

Для переведення додатного непарного числа (числа, молодший розряд якого є 1) потрібно спочатку представити його в двійковій канонічній системі з цифрами {0,1}. Потім, переглядаючи отримане представлення зліва направо, необхідно виділити всі групи цифр вигляду 00...01, навіть якщо вони включають тільки один нуль. Ці групи заміняють на групи вигляду 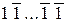, а інші одиниці залишають без зміни.

Для переведення від’ємного непарного цілого числа можливі два варіанти:

1) всі групи цифр вигляду 00...01 необхідно замінити на групи 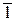1...11, а інші цифри 1 замінити на ;

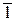2) всі цифри 1 замінюються на 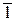, а потім групи цифр вигляду 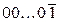необхідно замінити на групи 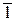1...11.

Приклад 2.13. Перевести двійкові числа 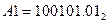і 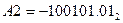в систему з основою 2 і цифрами {1,}.

Розв’язання. Використовуючи співвідношення (2.8), процес переведення додатного числа зводимо до заміни комбінацій 001, 01 комбінаціями відповідно 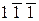і 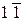, тобто .

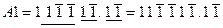Переведення від’ємного числа здійснимо двома способами:

1) ;

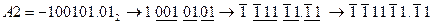2) .

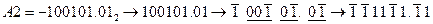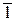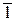Легко бачити, що з додатного числа відповідне відємне число (і навпаки) можна одержати шляхом заміни 1 на і на 1.

Парні числа (додатні чи від’ємні) можна перевести тільки наближено, тобто з певною похибкою або нескінченим дробом.

В зв’язку з цим для одержання скінченого подання як парних, так і непарних додатних чисел в системі {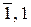} пропонується наступний запис чисел в системі {0,1}:

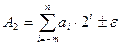, (2.9)

де 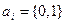, 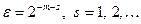– адитивна добавка, яку можна розглядати як похибку представлення чисел, яка вноситься перед переведенням чисел. Якщо , то маємо парне число і тоді адитивна добавка береться із знаком “+”, якщо 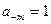, то маємо непарне число і тоді адитивна добавка береться із знаком “–”.

На основі (2.9), для переведення чисел в систему {1,} пропонується наступний алгоритм:

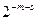· при переведені парного числа, в розряд , записують цифру 1 (що відповідає додаванню в (2.9) величини ) і роблять заміни комбінацій 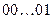на 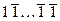з дописуванням в кінці (в розряд 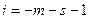) цифри ;

· у випадку непарного числа до заданого числа, в розряд , дописують цифру (що відповідає відніманню в (2.9) величини ) і роблять заміни комбінацій 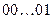на 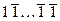, а комбінацію на 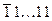з дописуванням в кінці (в розряд 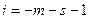) цифри 1;

Можна показати, що похибка перетвореного числа буде обчислюватись за формулами:

· для парного числа ;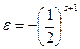

· для непарного числа .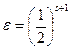

Приклад 2.14. Перевести в систему 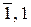цілі додатні числа (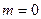): 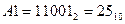і при .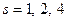

Розв’язання. Згідно з описаним вище алгоритмом будемо мати:

При :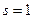

, ;

, .

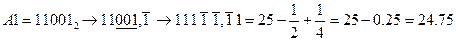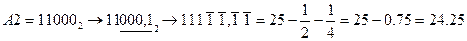При :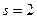

, ;

, .

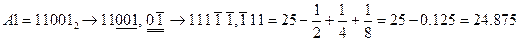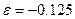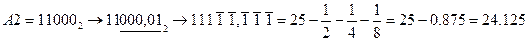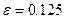При :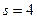

,;

, .

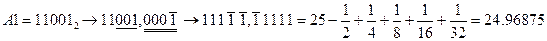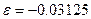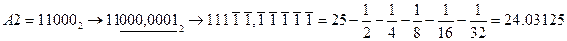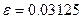З одержаних результатів бачимо, що абсолютна похибка переведення однакова як для непарних, так і парних чисел. Непарні числа переводяться з недостачею, а парні – з надвишком.

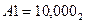
Приклад 2.15. Перевести в систему {1,} дробові числа: при .

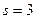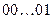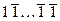Розв’язання. Спочатку підготуємо числа до перетворення, згідно із заданим параметром s. Після цього замінюємо в зображені числа комбінації на , а комбінацію на 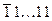з дописуванням в кінці (в розряд з номером 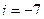) цифри і 1, відповідно. В результаті одержуємо:

, ;

, .

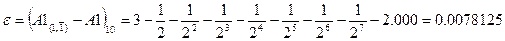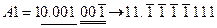У зв’язку з тим, що деякі числа в системі представляються неоднозначно, формулу (2.9) можна узагальнити, дописавши нулів перед старшим розрядом числа

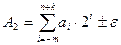, (2.10)

де .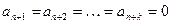

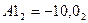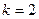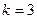Приклад 2.16. Перевести в систему числа і при , і .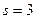

Розв’язання. Спочатку підготуємо числа до перетворення, згідно із заданими параметрами k і s. Після цього перетворюємо їх і обчислюємо похибку:

1. ,

,

;

,

.

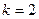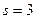
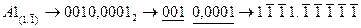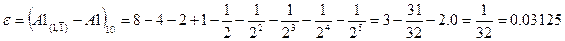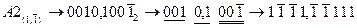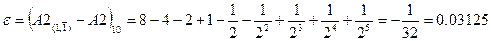2. ,

,

;

,

.

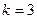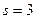
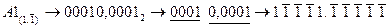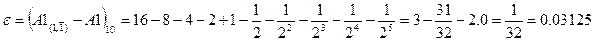Аналогічні результати можна дістати і для переведення від’ємних чисел, скориставшись правилом переведення від’ємних чисел.

Читайте також:

1. N – чисельність популяції
2. Аксіома неперервності дійсних чисел
3. Алгоритми переведення чисел з однієї позиційної системи числення в іншу
4. Аналіз чисельності, складу і руху персоналу
5. Біомаса - Кількість живої речовини на одиниці площі чи об'єму місцеперебування в момент спостереження. Визначається сумою біомаси усіх популяцій, що населяють дану екосистему.
6. В десяткову систему числення
7. В канонічну двійкову
8. Введення чисел.
9. Види переведення на іншу роботу
10. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
11. Визначення суми на множині цілих невід’ємних чисел, її існування та єдиність. Операція додавання та її основні властивості (закони).
12. Визначення чисельності окремих категорій працівників

Переглядів: 648