
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Середня величина.
Мода.
Модадля певної сукупності є значенням, яке домінує у цій сукупності.
Часто трапляються такі сукупності де певна варіанта зустрічається у переважній більшості елементів, а інші варіанти не такі поширені.
ПРИКЛАД. В Криму питома вага родин з різною кількістю дітей має наступну картину (2002р.):
| Кількість дітей | ||||||||
| % родин до загальної кількості | 10,0 | 25,0 | 55,0 | 8,0 | 1,3 | 0,5 | 0,1 | 0,1 |
Як видно з таблиці найбільш поширеною варіантою буде 2 дитини (55% родин від загальної чисельності).
Такі сукупності з певною натяжкою можна характеризувати одним числом – домінуючою (найбільш поширеною) варіантою - модою. Мода є домінантою, але не завжди “контрольним пакетом” . Тому не всі сукупності правомірно характеризувати саме модою.
ПРИКЛАД. Для сукупності А: 1, 2, 2, 5, 6, 10, 15, 100, 150, 200 модою буде 2.
Для сукупності Б: 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, модою теж буде 2.
Крім того модальна варіанта з однаковим успіхом може припадати як на найбільші, так і на найменші значення по сукупності. А тому в якості загальної характеристики мода може як занижувати, так і завищувати дійсний характер сукупності
ПРИКЛАД. Маємо дані про погодинну оплату праці (грн/год) на 12 посад у двох колективах.
Колектив А: 10, 10, 10, 10, 10, 20, 30, 30, 50, 100, 100, 250.
Колектив Б: 10, 10, 20, 20, 25, 25, 30, 70, 70, 70, 70, 90
Якщо охарактеризувати стан погодинної оплати праці в колективі А модою (10), то загальна картина того, як оплачується праця занижується, а у колективі Б (70) – навпаки завищується.
Якщо певна сукупність представлена графічно, як ряд розподілу, то для дискретних ознак моду легко знайти візуально (це буде вершина полігону). У безперервному ряду (на гістограмі) візуально можна виділити лише модальний інтервал (інтервал, що відповідає найвищому стовпчику). Зрозуміло, що мода буде знаходитись десь в межах цього інтервалу.
Коли при розрахунках треба уточнити де саме в цих межах вона знаходиться використовують наступну інтерполяційну формулу:
Мо = хо + h [(fо – f-1) / [(fо – f-1 )+(fо – f+1)]]
де хо – ліва межа модального інтервалу;
h – ширина модального інтервалу;
fо – висота модального стовпчику;
f-1 – висота передмодального стовпчику;
f+1 – висота післямодального стовпчику;
Зрозуміло, що це не дійсне значення моди, а число, яке беруть в якості її оцінки. Логіка цієї формули наступна: якщо схили гістограми навколо модального інтервалу симетричні, то в якості моди беруть значення, що відповідає середині цього інтервалу. Якщо несиметричні, то модальне значення від середини переміщується в сторону більш пологого схилу таким чином, що модальний інтервал поділяється модою в такому ж співвідношенні, як і величини: (fо – f-1) і (fо – f+1.). Іноді така оцінка себе виправдовує.
Основним недоліком моди в якості загальної характеристики сукупності є її “нечутливість” до зміни значень у інших елементів сукупності (звісно, якщо при цьому не з’явиться іншої моди). Тобто сукупність змінилася, потрібно очікувати і зміни показника, що її характеризує. Мода ж залишилась тою самою.
Тим не менш є ситуації, коли зручно користуватись наведеним показником. Мода важлива для виробників товару при встановлення цінової політики (для визначення які ціни є найбільш ліквідними), або для формування товарних запасів (наприклад за найбільш ходовими розмірами взуття, одягу, тари).
3. Медіана.
Медіана – це таке значення ознаки, яке поділяє сукупність на дві рівні частини таким чином, що одна половина елементів мають не перевищують це значення, а друга половина не нижчі за нього.
ПРИКЛАД. Для сукупності чисел: 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, 5, 6, 7, 9, 9. Медіаною буде 3. Перші сім елементів сукупності не перевищують це значення, а останні сім не нижчі за нього.
Для визначення медіани треба саму сукупність впорядкувати - вишикувати у порядку зростання і поділити навпіл. Як це було зроблено у наведеному прикладі. Центральний елемент і буде медіаною. Зрозуміло, що це можливе лише тоді, коли чисельність сукупності непарна. Інакше кажучи: коли чисельність сукупності непарна вона завжди має медіану серед своїх елементів. Якщо чисельність сукупності парна, то центральних елементів у сукупності виявляється два. Тоді в якості медіани беруть середню арифметичну цих двох центральних елементів (нагадуємо, що елементи сукупності при цьому треба попередньо розташувати у зростаючому порядку).
Медіана, в певному розумінні, це значення, що найближче розташоване до всіх елементів сукупності одночасно. Це означає, що сума модулів відхилень варіант сукупності від медіани мінімальна:
Σ |xi – Мe| fi = min
Цю властивість медіани використовують при розташуванні терміналів, заготівельних пунктів, зупинок транспорту і т. і.
ПРИКЛАД. Якщо певна організація планує побудувати низку автозаправок на трасі, що розташовані на відстанях х1, х2,х3, …, хn від міста. То нафтобазу потрібно розташувати на такому відстані від міста, яке є медіаною наведеної сукупності.
Медіану сукупності можна визначити, коли в наявності є графік кумуляти (огіви). Горизонтальна лінія, що проведена через вісь ординат в точці половини частоти, або частки перетинає графік огіви саме там, де на осі абсцис йому відповідає значення медіани.
 |
100 %


 50%
50%
 0% Ознака
0% Ознака
Коли в наявності є гістограма певної сукупності, то встановлення медіани зводиться до наступного:
- визначають медіанний інтервал (це буде перший інтервал, кумулятивна частота якого перевищує 50% від обсягу сукупності);
- в середині цього інтервалу визначають медіану за допомогою інтерполяційної формули:
Ме = хо + h [0,5 - S-1) / fме ]
де хо – нижня межа медіанного інтервалу;
h – ширина медіанного інтервалу;
S-1 – кумулятивна частка передмедіанного інтервалу;
fме – частка медіанного інтервалу (не кумулятивна);
Якщо гістограма зображена в координатах не ознака-частка, а ознака-частота, то у формулі будуть незначні заміни: замість 0,5 треба підставити половину обсягу сукупності, в якості S-1 – кумулятивну частоту передмедіанного інтервалу, а fме – частоту медіанного інтервалу.
Логіка формули полягає у наступному: висота стовпчику огіви, що стоїть на певному інтервалі, відповідає значенню ознаки на кінці, а не початку цього інтервалу. А зростання частоти (або частки) в межах цього інтервалу вважають рівномірним. Останнє припущення не обов’язково вірне, але дозволяє хоч якось визначитись в умовах відсутності відповідної інформації. Крім того при невеликих інтервалах групування похибка, що при цьому може виникнути, є незначною.
 Частка
Частка








 100%
100%
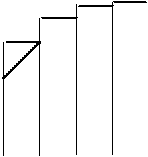 |




 50%
50%
 |

 0 Ознака
0 Ознака
Як не важко здогадатись дві половини сукупності, що розбиті медіаною рівні за своєю чисельністю, але можуть суттєво різнитись загальним обсягом ознаки (сумою варіант по кожній з половин). В деяких випадках це робить медіану нерепрезентативним показником.
ПРИКЛАД. Характеризувати медіаною споживання води будинками у районі міста, коли 55% району складає приватний сектор і 45% висотні будинки призведе до невірної уяви про цей район міста.
Тому інколи медіану доповнюють додатковими характеристиками – квартилями, що поділяють сукупність на чотири рівні частини, або децилями, що поділяють сукупність на десять рівних частин. При цьому суттєво уточнюються дійсний характер сукупності, але одночасно суттєво збільшується кількість необхідних для цього показників. Чого намагались уникнути на початку, до того повернулись.
Медіана більш суттєва характеристика ніж мода, оскільки є “центром” для всієї сукупності. А “центр” визначається загальним виглядом сукупності, хоч і не дозволяє її детально охарактеризувати. Основним недоліком медіани є її “нечутливість” до зміни значень у крайніх елементів сукупності.
Медіана є зручним показником для сукупності де невелика частина елементів значно відрізняються від загальної маси.
ПРИКЛАД. Треба оцінити дохід на родину у шахтарському містечку, де переважна більшість родин отримує менше ніж 1000 грн на місяць. Але в число мешканців входять володарі шахти, які отримують стільки ж, скільки всі інші разом взяті. Зрозуміло, що медіана в якості загальної оцінки доходу родини шахтарського містечка буде достатньо представницькою.
Один пішохід потрапляє під колеса
автомобіля кожні 17 хвилин. Бідолашний.
Я. Іпохорська.
Якби всі елементи сукупності робили рівні внески у загальний обсяг ознаки, то одним числом можна було б характеризувати всі елементи одразу. Але внесок одних більший, інших – менший. Тому ці різні елементи характеризують умовною величиною – середнім рівнем.
Для свого розрахунку середня величина вимагає двох конкретних параметрів:
- загального обсягу ознаки по сукупності;
- чисельності сукупності.
ПРИКЛАД – розрахунок середньої зарплати вимагає знання всього фонду оплати праці (загальний обсяг ознаки) і чисельності працівників. Середня вага виробу вимагає знання загальної ваги виробів (загальний обсяг ознаки) і кількості виробів. Середній тиск крові в колективі знання сумарного тиску по колективу (не несе самостійної змістовної суті) і чисельності колективу.
Для розрахунку середньої величини нам не потрібна інформація про значення ознаки у окремих елементів – нам потрібна величина загального обсягу ознаки по сукупності і чисельність елементів в сукупності.
Таким чином розрахунок середньої зводиться до відповіді на наступне питання: якщо загальний обсяг ознаки порівну (рівномірно) розподілити по всіх елементах сукупності, то яка величина ознаки припаде на кожний елемент?
Природі багатьох сукупностей притаманна властивість елементів групуватись навколо певного значення, яке дуже часто являє собою середній рівень ознаки по сукупності. Наявність у статистичній сукупності такого рівня є проявом статистичної закономірності. Ця закономірність пов’язана з загальною якістю, притаманною усім елементам сукупності та з умовами існування елементів сукупності.
ПРИКЛАД. Вартість об’єктів нерухомості залежить від самих об’єктів, та їх розташування. Рівень оплати праці залежить від самої праці та від країни де працюють.
Але середній рівень не обов’язково є тим значенням навколо якого відбувається групування. Середній рівень за своєю суттю – це результат штучної “урівняловки”. Він дорівнює тій величині, яка утвориться після виконання вимоги: загальний обсяг ознаки поділити на всіх порівну. Іноді це ефективний підхід, іноді не дуже.
ПРИКЛАД. Якщо у палаті шпиталю, де температура повітря складає 23˚С лежать чотири пацієнта з температурою 40˚С, а один помер і має температуру навколишнього середовища, то середня температура у пацієнтів цієї палати буде дорівнювати 36,6˚С.
Заміна множини індивідуальних значень сукупності на середню повинна відповідати основній умові: не змінювати загального обсягу явища. Тобто, якщо б кожний елемент сукупності мав би значення ознаки, що дорівнювало б середньому, то загальний обсяг ознаки по сукупності, при цьому, не зміниться.
Формально середніх є безкінечно багато, але практичне застосування мають не більше десятка з них, які по суті є різним проявом двох: середньої арифметичної, та середньої геометричної.
2.1.Середня арифметична.
Середня арифметична являє собою відношення сумарної величини всіх варіант ознаки до їх чисельності
х¯ = Σхι / n
Вона є самою простою і самою поширеною, оскільки переважна більшість сукупностей для визначення загального обсягу ознаки вимагають простої суми всіх варіант.
Дуже часто окремі варіанти в сукупності повторюються. У такому разі їх можна об’єднувати в групи, а загальний обсяг ознаки визначається, як сума добутків значень конкретної варіанти на її чисельність (частоту). Цей процес має назву зважування. Така середня арифметична має назву зваженої. Вона наочно демонструє, що значення середньої залежить як від величини варіанти так і від її чисельності. Вага кожної варіанти це її чисельність у сукупності.
х¯ = Σfіхι / Σfi
Середня арифметична зважена є просто іншою формою запису середньої арифметичної простої. За суттю вони ідентичні.
Властивості середньої арифметичної.
· Пропорційна зміна значень варіант викликає відповідну зміну середньої арифметичної.
· Пропорційна зміна ваг кожної варіанти не змінює середньої арифметичної.
· Сума відхилень індивідуальних значень елементів від середньої арифметичної дорівнює нулю
· Сума квадратів відхилень індивідуальних значень ознаки у елементів сукупності від їх середньої арифметичної менше, ніж від любого іншого значення.
2.2.Середня геометрична
Деякі явища характеризуються тим, що загальний обсяг ознаки по сукупності визначається не сумою елементів, а їх добутком.
ПРИКЛАД – розглядається сукупність років і спостерігають у скільки разів за кожний з цих років відбувалось зростання ціни на певний товар. Нехай буде така картина:
| Рік | 1-й | 2-й | 3-й | 4-й | 5-й |
| У скільки разів зросла ціна за рік | 1,20 | 2,00 | 1,30 | 1,05 | 2,10 |
Зрозуміло, що на протязі всіх 5-ти років ціна зросла в 7,65 рази. Значить визначення того як вона зростала в середньому за рік означає, що треба встановити таке число Z, що якби кожного року ціна зростала у Z разів, то за п’ять років вона якраз і зросла б у 7,65 рази.
Тому, коли загальний обсяг ознаки по сукупності формується, як добуток деяких величин, то середня знаходиться, як середня геометрична.
 Х = ʰ√ххх…х
Х = ʰ√ххх…х
2.3.Середня гармонічна.
Є ще один вид середньої величини, що використовують у статистиці – середня гармонічна.
Якщо маємо сукупність із n чисел: х1,х2, х3…х n, то середня гармонічна має вигляд:
n
 х¯ =
х¯ =
Σ (1/ хі)
Насправді середня гармонічна – це форма середньої арифметичної, яку вона приймає у окремих випадках. Досить часто трапляються такі сукупності, де чисельність певної варіанти пов’язана з її величиною зворотною пропорційністю (кількість товарів, вироблених за зміну обернена до часу на їх виготовлення, кількість товару, закуплена на фіксовану суму зворотньо залежить від ціни …).
ПРИКЛАД – три менеджери фірми на протязі робочого дня обслуговують клієнтів. Перший на клієнта витрачає 20 хв, другий 30 хв, а третій – 50 хв. . Скільки часу в середньому обслуговується один клієнт на цій фірмі?
Зрозуміло, що кількість клієнтів, що обслужив за день перший менеджер більша ніж у другого і тим більша ніж у третього. Маємо три варіанти ознаки (час обслуговування клієнтів) і їх частоти (чисельність клієнтів кожного менеджера). Вони пов’язані між собою оберненою залежністю.
Використати в якості відповіді на питання із прикладу середню арифметичну трьох чисел (20, 30 і 50) некоректно, бо кожний менеджер вносить різну “лепту” у створення сукупності клієнтів. Один швидко обслуговує і вносить суттєвий вплив, інший обслуговує повільно, відповідно клієнтів обслуговує мало, а значить і вплив клієнтів останнього на характер сукупності менш значний. Використання середньої арифметичної для трьох чисел можливо було б тільки тоді, коли кожний менеджер обслуговує за день однакову чисельність клієнтів (їх вплив однаковий). Інакше кажучи вся сукупність клієнтів складається з трьох груп, які обслуговувались трьома різними менеджерами, і ці три групи різні за своєю чисельністю.
Взагалі отримане середнє значення Y повинно відповідати наступній умові: якби кожний клієнт обслуговувався саме Y хвилин, то добуток середнього часу Y на фактичну чисельність клієнтів, що були обслужені повинен суворо дорівнювати загальні затрати часу менеджерів (для трьох це три робочих дні). Або навпаки: загальний час роботи менеджерів, поділений на середні затрати часу на одного клієнта повинен чітко дорівнювати такої самої кількості клієнтів, як і при реальній картині обслуговування (20 хв., 30 хв. і 50 хв.).
Так от, шляхом нескладних математичних перетворень знайдено, що при оберненій залежності у сукупності між частотою певної групи і її варіантою середня арифметична для сукупності дорівнює середній гармонічній для сукупності варіант.
Середня гармонічна носить назву простої, якщо сумарна величина ознаки по всіх групах (добуток окремої варіанти на її частоту) однакова.
Для наведеного прикладу – це робочий час менеджерів (добуток часу обслуговування одного клієнта на кількість клієнтів). Для всіх робочий день єдиний.
Якщо сумарна величина ознаки по всіх групах різна (кожен менеджер працює різний час), то розрахунок середньої набуває трохи інший вигляд і, за аналогією з середньою арифметичною носить назву середня гармонічна зважена:
Σ хі* fі
 х¯ =
х¯ =
Σ ( хі* fі / хі)
Такий підхід використовують, коли апріорі невідома чисельність кожної варіанти, але відома сама варіанта і відомий обсяг ознаки по кожній групі (скільки часу працював кожний менеджер).
Обсяг ознаки – це не вага. Це добуток ваги на значення варіанти.
2.4.Середня хронологічна.
Середня хронологічна використовується в умовах неповної інформації про динаміку явища.
ПРИКЛАД – постійно змінюється ціна на певний товар, температура повітря, валютний курс… І потрібно встановити середні (ціну, температуру, курс) за певний інтервал часу. Але в розпорядженні мають інформацією про значення параметру тільки в окремі моменти часу.
Якщо інтервали між моментами спостереження однакові, то середня хронологічна має наступний вигляд:
( х1+ хn)/2 + х1+ х1 +… +хn-1
 х¯ =
х¯ =
n-1
Подібний вигляд середньої отримують на підставі припущення, що між отриманими “моментними” значеннями відбувалась рівномірна зміна параметра. Тоді розрахунок середньої арифметичної для параметру, що змінюється за даним припущенням і дасть середню хронологічну.
Якщо інтервали між моментами спостереження різні, то враховують “вагу” інтервалів. Чим інтервал більший, тим він “вагоміший”. Такий підхід не зовсім коректний, але в умовах неповноти інформації треба якось визначатись. Тому в загальних випадках і погодились на подібне припущення.
(Лекція 4)
3. Характеристики варіації.
Любі зміни, навіть до кращого
Завжди пов’язані з незручностями.
Р. Хукер.
Варіація породжується комплексом різних умов і характеризує ступінь однорідності статистичної сукупності по певній ознаці. Чим менші відхилення індивідуальних значень одне від одного, тим однорідніша сукупність. Вимірювання ступеня коливання ознаки (варіації) – невід’ємна складова статистичного аналізу.
Ступень однорідність сукупності визначають по тому, як її елементи відхиляються від середнього рівня. Зрозуміло, що кожний по своєму. Але загальну однорідність сукупності якось треба визначати. Тому питання ставлять більш коректно: як в середньому відхиляються елементи сукупності від свого середнього рівня? Це певна абстрактна характеристика сукупності, яка ніяким чином не стосується жодного окремого елемента, а відноситься до всієї сукупності взагалі.
Варіація альтернативної ознаки умовно полягає в тому, що одні одиниці мають певну ознаку, а інші – ні.
Погодились вважати, що коли якісна ознака присутня у елементів сукупності, то її значення дорівнює 1, коли відсутня – 0.
 1111111111111111111110000000000
1111111111111111111110000000000
 р q N – чисельність всієї сукупності,
р q N – чисельність всієї сукупності,
 р – чисельність нормальної продукції,
р – чисельність нормальної продукції,
N q - чисельність бракованих виробів.
Однорідність сукупності за альтернативною ознакою характеризується долею ознаки р / N. Неоднорідність сукупності по альтернативній ознаці сягає від 0 до 50%.
3.1.Абсолютні характеристики:
1. Варіаційний розмах – відстань між максимальним і мінімальним значенням ознаки:
R = X max – X min.
2. Середнє абсолютного відхилення (лінійне відхилення)
Для того, щоб визначити, як в середньому елементи сукупності в відрізняються від свого середнього рівня треба скласти всі ці відхилення до купи і поділити цю суму на кількість елементів. Тобто яке відхилення в середньому припадає на один елемент. Але просто скласти нічого не дасть, бо відхилення зі знаком + будуть дорівнювати відхиленням зі знаком – (властивість середньої арифметичної). Тому складають модулі відхилень.
d = Σ│хі - х‾│/ n
3. Дисперсія.
У ХVІІІ ст., коли розроблялись статистичні методи комп’ютерів не було. І працювати з модулями було досить незручно. Тому класичний підхід для уникання “мінусів” полягає у піднесенні величин у квадрат. При цьому можна розрахувати “середній квадрат” відхилення ознаки від середнього арифметичного. Така величина називається дисперсією. Вона не зовсім очевидна для сприйняття, але достатньо інформативна щодо однорідності елементів. Чим більше елементів у сукупності значно відрізняються від середнього рівня, тим більшою буде дисперсія. Коли всі елементи зосереджені навколо середньої величини, то дисперсія буде мінімальною.
σ ² = [ Σ(хі - х‾)²] / n
Властивості дисперсії:
· Зменшення всіх варіант ознаки на одну й ту саму величину не змінює дисперсії.
· Зменшення всіх варіант ознаки в k раз зменшує дисперсію в k² разів.
4. Середнє квадратичне відхилення
Дисперсія хоч і є достатньо зручною характеристикою того, як взагалі елементи сукупності відрізняються від свого середнього рівня, але погано сприймається за своїм змістом. Дійсно якось важко второпати, що лінійну величину (відхилення від середнього рівня) потрібно характеризувати квадратичною. Тому часто застосовують не саму дисперсію, а корінь квадратний з неї. Ця величина носить назву середнє квадратичне відхилення.
 σ = √ σ ²
σ = √ σ ²
Середнє лінійне та середнє квадратичне відхилення за змістом ідентичні. Це іменовані числа. За величиною вони майже ніколи не співпадають. Більш зрозумілим є середнє лінійне відхилення, але більш поширеним у статистиці є середнє квадратичне відхилення. Все як у житті – штучне і не зовсім зрозуміле часто витісняє логічне завдяки зручності користування.
5. Дисперсія альтернативної ознаки.
 σ ² = Σ(хі - х‾)² / n, хі = 0, 1
σ ² = Σ(хі - х‾)² / n, хі = 0, 1
х‾ = 1+1+1…..+1+0+0+….+0 /N = p/N (у відносних одиницях - р)
σ ² = [(1-р) ²р + (0-р) ²q] / N
σ ² = р q
Легко встановити, що максимальне значення при цьому сягає 0,25 при р = q = 0,5
3.2. Відносні характеристики:
Коефіцієнт варіації.
· Лінійний : Vd = d / х‾
· Квадратичний: Vσ = σ / х‾
· Осціляції: VR = R / х‾
Коефіцієнт варіації є критерієм однорідності сукупності. В статистиці однорідною вважають таку сукупність, для якої квадратичний коефіцієнт варіації не перевищує 33% (якщо це не оговорюється окремо).
3.3. Умови однорідності сукупності, поділеною за альтернативною ознакою.
Традиційно сукупність вважається однорідною, коли її коефіцієнт варіації не перевищує 33%:
σ / х‾ < 33%.
Підставив значення σ і х‾ для альтернативних ознак отримаємо наступне:

 √ рq p < 0,33. pq / p² = 0,11 q / p = 0,11 q = 0,11 p
√ рq p < 0,33. pq / p² = 0,11 q / p = 0,11 q = 0,11 p
Таким чином сукупність, що поділена за альтернативною ознакою буде вважатися однорідною, коли одна якісна частина на порядок перевищує іншу. Причому ця умова симетрична: наприклад, якщо сукупність поділена на частини за ознакою брак, то однорідність може бути у розумінні , що майже вся сукупність бракована, або майже вся сукупність якісна.
(Лекція 5)
Тема 5. Характеристики розподілу.
Зазвичай істина лежить посередині.
І в більшості випадків без пам’ятника.
С. Є. Лець
1. Форма розподілу.
Незважаючи на свою універсальність середні величини не завжди є достатньо інформативними, щодо сукупності:
ПРИКЛАД. Твердження, що середня температура у хворих в палаті становить 36,6° може означати що:
· або всі здорові,
· або у одних пацієнтів жар, а інші вже померли і мають температуру повітря в палаті.
Коли вимоги до аналізу сукупності достатньо високі, то навіть доповнення середніх величин загальними характеристиками варіації (такими, як розмах, дисперсія та іншими) виявляється недостатнім.
Найбільш вичерпним описанням сукупності буде таке, коли наводиться “вагомість” кожної варіанти. Інакше кажучи встановлюється яких значень більше (і у скільки разів) ніж інших в межах варіаційного розмаху. Саме таку інформацію і надають за допомогою полігона або гістограми. Висота стовпчиків гістограми і буде давати уяву про кількісний розподіл сукупності в межах відповідних значень ознаки. Ламана, що проходить через середини верхівок стовпчиків гістограми утворює певну характерну форму. Зменшуючи інтервали групувань (ширину стовпчиків) ця форма набуває більш “впевненого” вигляду, який і відбиває загальну картину сукупності, що досліджується. Це і називається встановити форму розподілу. Таким чином форма розподілу дає загальну уяву про те які значення і в якій кількості зустрічаються у сукупності.
Слід зауважити, що форма розподілу є характеристикою сукупності якоюсь одною ознакою і для тієї ж самої сукупності елементів форми розподілу за іншими ознаками можуть суттєво різнитись.
ПРИКЛАД- одне і теж саме населення по різному буде розподілятись за віком, зростом, доходом, національністю, інтелектом.
Зрозуміло, що чим меншим буде інтервал групування при побудові гістограми, тим детальніше буде передаватись форма розподілу статистичної сукупності.
Форми гістограми, або полігону є достатньо інформативними щодо властивостей сукупності: вони дозволяють спостерігати варіаційний розмах ознаки, співвідношення частот різних варіант, навіть дозволяють визначити середнє значення, моду, медіану, дисперсію, а також розрахувати багато інших кількісних характеристик. Творець кібернетики Н. Вінер називав статистику наукою про розподіли.
ПРИКЛАД – розподіл безробітних за віком (Київ 2000р.).
| Вікова група | До 20 | 20-25 | 25-30 | 30 -35 | 35 -40 | 40 -45 | 45-50 | 50-55 | 55-60 |
| % |
 |






 20
20
 |

 10
10
 | |||
 |

 5
5
 |
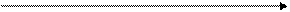 20 25 30 35 40 45 50 55 60
20 25 30 35 40 45 50 55 60
Форма розподілу відбиває певний стан статистичної сукупності, який формується під впливом внутрішніх факторів (тобто властивостей самих елементів), та зовнішніх (умов існування сукупності). Спільна дія цих чинників, в загальному випадку, і визначає як межі, в яких змінюється ознака (діапазон), так і кількісний розподіл відповідних значень(висоту стовпчиків гістограми) .
Для подальших висновків реальну форму розподілу (“гістограму” або “полігон”) замінюють (апроксимують) підходящим аналітичним виразом, що дозволяє залучити до аналізу готовий апарат математичної статистики. Тобто реальний розподіл моделюємо ідеальним.
Теоретичних законів (стандартних форм) розподілу, що використовують у статистиці, налічується близько тридцяти. Як це не дивно, безліч різних за своєю природою статистичних сукупностей проявляють настільки схожі форми гістограм, що в більшості випадків всі їх можна звести до цих трьох десятків теоретичних законів. Цього достатньо для описання різних за своєю природою сукупностей: від розподілу галактик у всесвіті до розподілу хабарів у окремому відомстві. Мабуть Піфагор не помилявся, коли казав, що світом правлять числа.
Вигляд деяких теоретичних розподілів наведено нижче:
| Рівномірний | Експоненціальний | Хі-квадрат | Сімпсона | Накагамі | Арксинуса | Гамма-розподіл |
   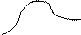                    
|
2. Нормальний розподіл
В багатьох, різних за своєю природою, сукупностях можна спостерігати наявність певного середнього рівня ознаки навколо якого групується більшість елементів сукупності. Причому чим більше ті, чи інші варіанти відрізняються від цього середнього рівня, тим менше вони зустрічаються. Детальні дослідження встановили, що у більшості випадків ознака у таких сукупностях розподілена за характерною симетричною “дзвоноподібною” формою. Таку форму назвали нормальним розподілом (інша назва – розподіл Гауса). Поняття нормального розподілу покладено в основу багатьох методів статистики.
ПРИКЛАД – вага, зріст людини, характеристики промислових виробів (розмір, вага, опір, пружність, ресурс). Всі ці ознаки розподілені за нормальним розподілом.
Використання напрацювань математичної статистики дозволяє залучати готові підходи для кількісного аналізу закономірностей суспільних явищ.
ПРИКЛАД – якщо встановлено, що розподіл певної ознаки по сукупності підкоряється нормальному закону, то можна оцінити долю елементів сукупності, що відрізняються від середнього значення на величину кратну СКВ.
σ: =0,68269
2 σ = 0,95450
3 σ = 0,99730.
Іншими словами, при розподілі Гауса 68% елементів сукупності відрізняються від середнього рівня на величину не більшу заσ, а 95% елементів відрізняються від того ж середнього рівня на величину не більшу за 2σ. Для інших розподілів ці співвідношення можуть бути іншими.
3. Характеристики форми розподілу
Аналіз закономірностей розподілу дозволяє кількісно оцінити ступень однорідності сукупності і обрати ті чи інші методи статистичного дослідження. В однорідних сукупностях розподіли одновершинні (одномодальні), оскільки вплив різних факторів призводить до виділення певної домінуючої варіанти у сукупності біля якої групуються всі інші. Багатовершинність (полімодальність) свідчить про неоднорідний склад сукупності. Описати багатовершинні розподіли теоретично важко. У такому разі необхідно перегрупувати дані, відокремити однорідні групи.
Одновершинний розподіл може бути симетричним та асиметричним (коли вершина зміщена). Асиметрія буває лівостороння та правостороння. Напрям асиметрії протилежний напряму зміщення вершини (за правилом хвоста), Асиметрія виникає під впливом домінуючої причини, яка обмежує варіацію в одному напрямку.
У суспільних процесах це може відбуватись навмисно.
Симетричний розподіл: хˉ = Мо = Ме
Правостороння асиметрія: хˉ >Ме>Мо
Лівостороння асиметрія: хˉ <Ме<Мо.
Чим більша асиметрія тим більше відхилення хˉ-Мо. Тому за міру асиметрії іноді беруть коефіцієнт скошеності (відносне відхилення): хˉ-Мо.
А = -------
σ
Правостороння: А>0, лівостороння: А<0.
Теоретично відносне відхилення не має меж, а на практиці не перевищує одиниці.
ПРИКЛАД –Рівень забезпеченості житловою площею міського населення України, доходи населення
Строге оцінювання характеру розподілу базується на, так званих, центральних моментах розподілу. Це поняття запозичене з механіки. Моменти у механіці визначають ефективність дії різних сил для надання тілу обертального руху. Моменти в статистиці характеризують загальний вплив зовнішніх і внутрішніх чинників, які формують величину і розподіл варіант по сукупності.
Математично момент – це середня арифметична r-того ступеня відхилення індивідуальних значень ознаки від середньої.
σ ² = [ Σ(хі - х‾)ʳ ] / n
Момент 2-го порядку – це дисперсія.
Момент 3-го порядку – це коефіцієнт асиметрії
Момент 4 -го порядку – це ексцес.
Коефіцієнт асиметрії:
Характеризує наскільки форма розподілу несиметрична.
Аs = [ Σ(хі - х‾)³ ] / n
В залежності від того як сильно зміщена мода розрізняють три ступеня асиметрії в розподілі
Низька – Аs < 0,25
Середня – Аs = 0,25 – 0,5
Висока - Аs > більше 0,5
Ексцес:
Якщо в центральному моменті розподілу обрати ступень 4, то отримаємо наступну характеристику – ексцес (відхилення від норми). Він характеризує ступінь зосередженості елементів навколо центру розподілу. За норму береться розподіл Гауса (нормальний закон), для якого величина ексцесу дорівнює 3.
Більш однорідні сукупності (Ek < 3) дають плосковершинний розподіл, а відповідно більш неоднорідні сукупності (Ek > 3) дають гостровершинний розподіл.
Нормальний Ek = 3
Гостровершинний Ek > 3
Плосковершинний: Ek < 3
(Лекція 6)
Тема 5. Вибіркове спостереження.
Складних наук нема.
Є погане викладення.
А. Герцен.
1. Уява про вибіркове спостереження
При статистичному дослідженні досить часто доводиться обмежуватись спостереженням не всієї сукупності, а певної її частини. Причин цьому багато:
- неможливість суцільного спостереження;
- значні затрати на його виконання;
- стислі терміни обробки даних;
- перевірка результатів суцільного спостереження.
ПРИКЛАД – опитування перед виборами.
Вибірковим називають такий вид спостереження, при якому обстеженню підлягають не всі одиниці сукупності, а тільки певна їх частина, відібрана у випадковому порядку.
Генеральна сукупність – це сукупність елементів, щодо якої потрібно зробити висновки на підставі вибіркового спостереження.
Вибіркова сукупність – частина генеральної сукупності, що надана для статистичного спостереження.
Мета вибіркового спостереження - по характеристиках вибірки зробити висновки про всю генеральну сукупність. Але розповсюдження характеристик вибірки на генеральну сукупність ставить питання наскільки це правомірно?
В загальному випадку ці характеристики цих двох сукупностей не співпадають. Така відмінність статистичних характеристик носить назву помилки репрезентативності. Кожна вибіркова сукупність за своїми показниками буде в тій, чи іншій мірі відрізнятись від генеральної. І чим більша варіація ознаки у генеральній сукупності, тим ці відмінності можуть бути більшими.
Взагалі з певної генеральної сукупності можна отримати безліч (точніше майже безліч) різноманітних вибіркових сукупностей.
ПРИКЛАД –якщо генеральна сукупність містить n елементів, а вибіркова m, то кількість можливих різних вибірок дорівнює: n !
 m!(n-m)!
m!(n-m)!
При n =15, а m = 5 загальна кількість різних вибіркових комбінацій дорівнює z = 3003.А якщо обсяг вибіркової сукупності можна взяти любим від 1 до n, то можливих вибірок стає ще більше.
Генеральна сукупність і кожна з можливих вибіркових характеризуються своїми конкретними показниками: долею, середньою величиною, дисперсією…
Метод вибіркового спостереження зручніше розглянути на прикладі.
ПРИКЛАД . На ринку нерухомості м. Києва виставлено на продаж n однокімнатних квартир (генеральна сукупність). Зрозуміло, що у цій сукупності є якась найдешева квартира Хmin і найдорожча Хmax. Ця сукупність характеризується двома наступними показниками : середньою ціною Хˉ(дає уяву про рівень цін) і дисперсією σo² (характеризує однорідність ринку нерухомості).
Якщо ми візьмемо різні можливі вибірки квартир із генеральної сукупності чисельністю від 1 до m, то кожна з них буде характеризуватись своєю середньою ціною Х˜ і своєю дисперсією σв².
2 . Види та схеми відбору.
Існують різні види та схеми відбору, їх особливості впливають на методи обчислення помилки репрезентативності.
Види відбору:
Простий випадковий – здійснюється за допомогою жереба.
Систематичний (механічний) – здійснюється через рівні інтервали від першого елемента. Перший обирається випадково.
Типовий – здійснюється розбиттям сукупності на типові групи. Потім з кожної групи за одним з перших двох видів відбирається кількість одиниць, пропорційна питомій вазі групи у загальній генеральній сукупності.
Серійний - здійснюється шляхом відбору не окремих одиниць, а цілих серій за одним з вище наведених методів.
Комбінований – різні комбінації попередніх видів.
Схеми відбору:
Повторний відбір – при цьому кожна відібрана одиниця повертається у сукупність і може знов потрапити у вибірку.
Безповторний – Безповторний відбір – кожна відібрана одиниця не повертається у сукупність.
Одним з різновидів вибіркового спостереження є моментне спостереження. Воно вибіркове за часом і суцільне за охопленням сукупності. В якості генеральної сукупності виступає час існування певного об’єкту чи процесу, а вибірки – час спостереження.
3. Парадигма вибіркового методу.
Розглянемо сукупність всіх можливих середніх вибіркових цін Х˜. Це нова сукупність. Її створюють можливі комбінації із первісної сукупності. Виявляється, що вибіркові середні значення Х˜ , які з’являються у кожній комбінації розподіляються за нормальним законом. Вісь симетрії при цьому перетинає по осі абсцис значення, що відповідає значенню генеральної середньої.
При цьому не має значення яку форму мав розподіл ознаки у генеральній сукупності. Не треба плутати ці два розподіли: розподіл ознаки по генеральній сукупності і розподіл середніх вибіркових значень.
Середні вибіркові значення із любої сукупності чисел завжди розподілені за нормальним законом. Інакше кажучи переважна частина середніх вибіркових значень групуються навколо середнього значення генеральної сукупності. Вибірки, що дають середню ціну значно відмінну від генеральної з’являються не часто. І чим більша така відмінність, тим менше таких вибірок.
Відомо, що коли сукупність розподілена за нормальним законом, то її завжди можна розбити на дві групи, за величиною того, як вони відрізняються від середнього рівня. Причому співвідношення цих груп вже давно відомі. Інтервали групування при цьому кратні середньоквадратичному відхиленню (СКВ) такого розподілу.
Для нашого прикладу це означає:
1. Середні ціни можливих вибірок утворюють велику сукупність чисельністю z, що розподілена за нормальним законом.
2. Для цієї сукупності, як і для всякої іншої можна розрахувати СКВ. За традицією СКВ для середніх вибіркових значень позначають літерою μ.
μ ² = [Σ(х˜і - х‾)²] / z
3. Можна стверджувати, що із всієї сукупності можливих вибірок 68,3% дадуть середню ціну, що відрізняється від середньої ціни по Києву на величину не більшу + μ і 31,7% вибірок дадуть середню ціну, що відрізняються від середньої по Києву на величину більшу за + μ.
4. 95,4% вибірок дадуть середню ціну , що відрізняється від середньої ціни по Києву на величину не більшу за + 2μ і 4,6% вибірок дадуть середню ціну, що відрізняються від середньої по Києву на величину більшу за + 2μ.
5. 99,7% вибірок дадуть середню ціну, що відрізняється від середньої ціни по Києву на величину не більшу за + 3μ і 0,3% вибірок дадуть середню ціну, що відрізняються від середньої по Києву на величину більшу за + 3μ.
Різниця між дисперсією ознаки у генеральній сукупності і дисперсією для середніх вибіркових значень показана у наступному прикладі.
ПРИКЛАД. На ринку нерухомості продається 8 однокімнатних квартир, що розподілені за рівномірними законом: 2 шт. – 10000$, 2 шт. – 11000$, 2 шт. – 12000$,2 шт. – 13000$. Для дослідження надаються любі чотири квартири.
Дисперсія, що характеризує варіацію ціни у цій сукупності квартир:
σ ² = [(10000-11500)²*2 + (11000-11500)²*2 + (12000-11500)²*2 + (13000-11500)²*2] / 8
8 – це кількість квартир у генеральній сукупності.
Дисперсія, що характеризує варіацію вибіркових середніх:
μ ² = [(10500 –11500)² + (10750-11500)²+ …….. +(12250-11500) ² + (12500 – 11500)²] / 70
70 – це кількість можливих вибіркових комбінацій
Параметр μ несе подвійну інформацію.
По-перше, оскільки це СКВ вибіркових середніх, то він характеризує як в середньому відрізняється середнє значення генеральній сукупності і середні значення по всіх можливих вибірках. Завдяки цьому параметр μ має назву середня помилка вибірки. Зустрічається також назва стандартної помилки.
По-друге, оскільки вибіркові середні величини розподіляються за нормальним законом, то можна стверджувати, що більше ніж 68% вибірок зі 100% можливих будуть давати середню величину, що відрізняється від середнього значення генеральній сукупності на величину не більшу за μ.
Тому, коли ми отримаємо яку завгодно вибіркову сукупність і визначаємо для неї середнє значення, то можна стверджувати, що воно має більше 68 шансів зі 100 бути з діапазону х¯ген + μ, і, відповідно менше 32 шансів зі 100 бути за межами цього діапазону (тобто різнитись на величину більшу ніж μ ). Нормальний розподіл вибіркових середніх дозволяє визначити ймовірність того що наша окрема вибіркова середня величина відрізняється від невідомої генеральної середньої на величину не більшу кратній μ.
Це означає, що стверджуючи, що різниця між любою вибірковою середньою і генеральною середньою величиною не перевищує :
1 μ – ми помиляємось у 31,7% випадків зі 100%,
2 μ – ми помиляємось у 4,6% випадків зі 100%,
3 μ – ми помиляємось у 0,3% випадків зі 100%.
В цьому і міститься сучасна парадигма вибіркового методу: отримані в кінці-кінців оцінки не є ані однозначними, ані стовідсотково достовірними. Вказується лише діапазон в якому з певною ймовірністю може знаходитись потрібна нам оцінка. Цей діапазон носить назву довірчого інтервалу.
(Лекція 7)
Чужа думка вважається ясною тоді,
коли власні думки ще більш незрозумілі.
М. Пруст.
2. Помилки вибірки.
Вибіркові оцінки надаються у вигляді довірчого інтервалу, який, в певному розумінні, визначає їх точність. Його величина кратна μ, тому останню і називають стандартною похибкою (помилкою). А кожну з половинок довірчого інтервалу називають граничною похибкою (помилкою).
Гранична помилка вибірки – це максимально можлива помилка для взятої ймовірності. Формула граничної похибки (помилки):
Δ = tμ (t – коефіцієнт пропорційності).
Гранична помилка вибірки задає діапазон, де з певною вірогідністю має знаходитись відповідний показник для генеральної сукупності – так званий довірчий інтервал. Коефіцієнт пропорційності t, що зв’язує Δ і μ має назву коефіцієнта довіри.Тобто знайшовши середнє вибіркове значення ми можемо навколо нього вказати довірчий інтервал, де з певною ймовірністю знаходиться невідомий генеральний параметр. Величина ймовірності і інтервал взаємопов’язані. При збільшенні заданої ймовірності оцінок інтервал їх можливого знаходження на жаль збільшується. І навпаки.
Розподілу Гауса підкоряються не тільки кількісні середні показники (як-то середня ціна, вага, ресурс, собівартість, тривалість життя…), але і доля розподілу (для альтернативної ознаки).
ПРИКЛАД- маємо сукупність n виробів. З них q – відсоток бракованих. Якщо з цієї (генеральної) сукупності ми візьмемо різні вибіркові сукупності виробів чисельністю від 1 до m (m< n ) і кожного разу встановимо долю браку у вибірці, то так само отримаємо певну сукупність відсотка браку по можливих вибірках, що може лежати в межах від 0% до 100%. Якщо ми побудуємо гістограму розподілу вибіркового відсотку браку, то виявиться, що цей розподіл теж близький до нормального. Причому вісь симетрії цього розподілу відповідає значенню q для генеральної сукупності.
Вибірковий метод побудований на використанні властивостей нормального розподілу. Вимірюють (а точніше оцінюють) розбіжність між вибіркою і генеральною сукупністю за допомогою стандартної похибки вибірки μ. Зрозуміло, що останню неможливо знаходити, як традиційне СКВ статистичної сукупності (бо це вимагає знання середнього значення всіх можливих вибіркових сукупностей і самої середньої величини по генеральній сукупності, а вибіркове спостереження як раз застосовують там, де нема повної інформації).
Як доведено в теорії вибіркового методу дисперсія вибіркових середніх у m разів менша від дисперсії ознаки у генеральній сукупності.
μ ² = σ²ο /m
Зрозуміло, що в загальному випадку, σ²ο невідома (оскільки вимагає знання всіх варіант генеральної сукупності, а отже яке це тоді вибіркове спостереження). Тому на практиці використовують не саме значення σ²ο, а її приблизну незсунену оцінку, яка грунтується на зв’язку дисперсій генеральної σ²ο і вибіркових σв² сукупностей.
Для повторної:
σ²ο = σв² m /(m-1)
Для безповторної:
σ²ο = σв² (n-m) / (n-1)
Ще один підхід - використання оцінки σ²ο за аналогією з попередніми дослідженнями.
Коли неможливо скористатись оцінками за аналогією то намагаються робити пробні обстеження,щоб скористуватись коефіцієнтами Пірсона.
Пірсон досліджував у різних статистичних сукупностях зв’язок між σ і R. Він знайшов, що у багатьох випадках простежується пропорційна залежність між σο і, так званим, Ŕ cер, який являє собою середнє значення групового варіаційного розмаху. Тобто якщо певну сукупність розбити на групи чисельністю d, то кожна група буде мати свій варіаційний розмах. Середнє арифметичне з них і дає Ŕ cер.
σο ≈ k(d) Ŕ cер.
Ккоефіцієнт k змінюється в залежності від обсягу сукупності групи d. Пірсон довів, що в якості грубих оцінок можна прийняти такі значення коефіцієнту пропорційності.
| d | |||||||||||
| k | 0,43 | 0,32 | 0,27 | 0,26 | 0,24 | 0,23 | 0,22 | 0,20 | 0,18 | 0,17 | 0,17 |
На практиці це виглядає так:
- генеральну сукупність розбивають на рівні частини;
- для кожної групи знаходять варіаційний розмах;
- розраховують середній розмах;
- знаходять СКВ, скориставшись середнім розмахом і коеф. Пірсона.
Якщо апріорно відомо, що генеральна сукупність підкоряється нормальному закону, то з ймовірністю 0,997 можна стверджувати, що
6СКВ = R.
Це окремий випадок, але дуже розповсюджений.
Маючи оцінку дисперсії ознаки у генеральній сукупності σ²ο і чисельність вибірки m можна отримати значення стандартної помилки вибірки μ. Після цього задаючись потрібною ймовірністю щодо оцінки середньої величини у генеральній сукупності можна отримати відповідні граничні помилки вибірки.
 Δ = tμ = t σο / √m
Δ = tμ = t σο / √m
Пропорційний зв’язок між стандартною і граничною помилками вибірки призводить до того, що остання залежить від:
· Загальної варіації ознаки у генеральній сукупності;
· Обсягу вибірки;
· Узятого рівня вірогідності оцінок.
4. 1. Репрезентативна помилка альтернативної ознаки.
Помилка вибірки альтернативної ознаки - це невідповідність розподілу долі у вибірці та генеральній сукупності.
ПРИКЛАД – існує реальна картина розподілу електорату у країні (pο, qο ). Здійснюється вибіркове опитування. Встановлюють вибіркові значення (p, q). Треба оцінити частку pοі qοу генеральній сукупності.
Розходження часток (долі) у вибіркових сукупностях від долі у генеральній сукупності також підкоряється нормальному закону (точніше близьке до нормального).
Тому для знаходження долі ознаки у генеральній сукупності потрібно знайти середню помилку вибірки μ, а далі з певною ймовірністю можна вказати довірчий інтервал де буде знаходитись відповідна частка у генеральній сукупності.
Оскільки дисперсія альтернативної ознаки у генеральній сукупності невідома, то аналогічно застосовують оцінки на підставі вибіркової дисперсії.
Для повторної:
σ²ο = pοqο = pq m /(m-1)
Для безповторної:
σ²ο = pοqο = pq (n-m) / (n-1)
Всі підходи, що були застосовані для знаходження середньої величини у генеральній сукупності підходять і для знаходження частки. Треба тільки зробити заміну:
σв²= pq
Підсумовуючи все вищенаведене можна зазначити наступне:
· Частіше за все вибіркове спостереження має на меті встановлення середнього значення певної ознаки по сукупності, або частки за альтернативною ознакою.
· Це значення вказується не точно, а у вигляді певного довірчого інтервалу, де з певною ймовірністю знаходиться невідомий параметр. Цю вірогідність можна брати якою завгодно.
· Гранична помилка, що визначає межі довірчого інтервалу є величиною, кратною μ - СКВ вибіркових середніх (або вибіркових часток).
· Стандартна похибка вибірки μ однозначно пов’язана з дисперсією ознаки у генеральній сукупності і чисельністю самої вибірки: μ ² = σ²ο /m
· При оцінюванні дисперсії ознаки у генеральній сукупності σ²ο за допомогою дисперсії ознаки у вибірці σв² потрібно враховувати схеми відбору (повторний, або безповторний).
Задачі.
1. На підставі розподілу аудиторії за статтю встановити долю хлопців і дівчат серед всіх студентів УАЗТ (Р=0,90).
2. Визначити середню тривалість життя по регіону, якщо для вибірки отримані наступні дані (Р=0,95):
| До 20 | 20-40 | 40-60 | 60-80 | 80 і більше |
(Лекція 8)
5 . Відносна похибка вибірки.
З тих пір, як за теорію відносності взялись
математики, я вже сам її більш не розумію.
А. Ейннштейн.
Гранична похибка вибірки задає довірчі межі в яких з певною ймовірністю знаходиться відповідна характеристика генеральної сукупності. Це означає, що з певною ймовірністю можна стверджувати, що різниця між невідомою реальною величиною і отриманою оцінкою (у вигляді інтервалу) може бути від 0 (мінімальна різниця) до величини граничної похибки (максимальна різниця). Інакше кажучи гранична похибка визначає точність отриманої оцінки.
Похибка вимірюється у тих самих одиницях, що і сама характеристика і являє собою абсолютну величину. Для середньої величини тут все зрозуміло. А для частки маленьке зауваження. Оскільки частка вимірюється у відсотках, то і її гранична похибка вимірюються у відсотках.
Втім використання граничної похибки у вигляді абсолютної величини не завжди зручне коли треба порівняти похибки вибірки різних ознак в одній і тій самій генеральній сукупності, або однієї і тієї самої ознаки у різних сукупностях.
ПРИКЛАД . Дві методики дозволяють визначити дохід на душу населення в з точністю +-70$. Чи правомірно їх застосувати до таких країн, як Україна, Марокко і Канада.
Часто цікавить не саме абсолютне значення граничної похибки, а його співвідношення з середнім рівнем, або часткою. Тобто на скільки % ми можемо помилитись в оцінці потрібного нам показника у генеральній сукупності у порівнянні з отриманою величиною по вибірці.
ПРИКЛАД – на передодні виборів робиться опитування. Поставлене завдання: чи подолають певні партії 4% бар’єр? Постає питання: з якою точністю повинно бути зроблене статистичне дослідження (тобто яка гранична похибка вибірки)? Якщо вибіркова частка складає 50%, то значення граничної похибки 45% забезпечить відповідь на поставлене завдання, а якщо вибіркова частка становить 7%, то і 4,5% не влаштують.
Порівнюються дві країни за середнім доходом на душу населення з точністю +-100$. Вибіркові обстеження дали наступні результати: у першій країні середній дохід на душу знаходиться в межах 150+-100$, а по другий – 1500+-100$. Зрозуміло, що по першій країні при такій самій граничній помилці (+-100$) неможливо зробити однозначних висновків.
Такі порівняння виконують за допомогою відносної похибки, яка показує на скільки % вибіркова оцінка може відхилятися від потрібного нам параметра генеральної сукупності (за умов певної ймовірності). Зрозуміло, що за 100% взятий середній рівень ознаки у генеральній сукупності.
Відносна стандартна похибка вибірки– це коефіцієнт варіації вибіркових середніх значень.
Vμ =μ / хˉ (100%)
Її можна розрахувати і на основі коефіцієнта варіації ознаки (якщо він відомий).
 |
Vμ = V/ √m
Ця величина носить двоякий зміст:
1. Оскільки μ – це середньоквадратичне відхилення вибіркових середніх, то Vμ показує на скільки відсотків в середньому кожне з середніх вибіркових значень відрізняється від середньої величини по генеральній сукупності.
2. Оскільки сукупність вибіркових середніх значень розподілена за нормальним законом, 68% вибіркових середніх значень і генеральне середнє значення будуть розрізнятись на величину, що не перевищує Vμ відсотків, а 32% вибіркових середніх на в
Читайте також:
- VI. Середня кишка
- VІ Середня хронологічна
- Безпосередня і представницька демократія
- Видаток і середня швидкість ламінарного потоку.
- Ефективний діаметр молекул. Частота зіткнень та середня довжина вільного пробігу молекул
- Загальна середня освіта.
- І Середня арифметична проста
- ІІ Середня арифметична зважена
- ІІІ Середня гармонічна
- Середня арифметична з відносних величин
- Середня геометрична
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 3. Зведення статистичних даних. | | | ПРИКЛАД. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |