
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ПРИКЛАД.
Б)
А)
Задача
1. Скільки респондентів треба обстежити перед виборами при опитуванні, щоб гарантувати похибку не більше 2% при ймовірності Р=0,99. Про апріорний розподіл електорату нічого не відомо.
2. Чи достатньо обстежити 1000 родин в місті, щоб встановити середній дохід на родину з точністю +- 20 грн., якщо в місті мешкає 70000 родин. Результати виявились наступні:
| До 200 грн | 200-400 | 400-600 | 600-800 | 800-1000 | 1000-1200 | 1200 і більше |
| 2% | 20% | 40% | 20% | 10% | 5% | 3% |
7. Мала вибірка
Зрозуміло, що точність вибіркового спостереження зростає з ростом вибірки ( при цьому зменшується μ, а відповідно і Δ) і навпаки. Але це вірно тільки до певної межи. Встановлено, що коли вибірка зменшується до 30 одиниць і нижче (таку вибірку звуть малою), то закон розподілу вибіркових середніх вже не є нормальним.
Англійський статистик Стьюдент (Госсет) довів, що розподіл вибіркових середніх, коли обсяг вибірки не перевищує 30 одиниць має свій окремий закон розподілу - розподіл Стьюдента. Така вибірка зветься малою.
Мала вибірка не так добре віддзеркалює властивості генеральної сукупності (не є репрезентативною).
Дисперсія середніх вибіркових значень для розподілу Стьюдента і дисперсія ознаки у генеральній сукупності пов’язані наступним чином:
μ² мв = σο² ⁄ m -1
Стьюдент дослідив, якими будуть вірогідності того, що генеральна середня величина буде відрізнятись від вибіркової середньої величини (для малої вибірки) на величину +- μ мв, +- 2μ мв, +- 3μ мв. І знайшов, що ці ймовірності будуть меншими за ймовірності нормального розподілу і на відміну від розподілу Гауса залежать від обсягу малої вибірки).
 m t m t
| ||||||||
| 0,356 | 0,644 | 0,656 | 0,666 | 0,670 | ||||
| 0,884 | 0,898 | 0,908 | 0,914 | 0,919 | 0,924 | 0,936 | 0,940 | |
| 0,960 | 0,970 | 0,976 | 0,980 | 0,983 | 0,984 | 0,992 | 0,992 |
Тому, коли тільки можна, то треба уникати малої вибірки.
Задача на середній зріст, час поїздки до УАЗТ,
(Лекція 9)
Закрийте двері перед всіма помилками
І істина вже ніколи не зможе зайти.
Р. Тагор.
8. Поняття про статистичну перевірку гіпотез.
Статистичні гіпотези – це певні припущення щодо властивостей сукупності. В загальному випадку ці припущення формулюють у вигляді двох гіпотез:
1. Нульова гіпотеза (Нο): сукупність відповідає певним умовам (нульовою вона зветься тому, що передбачає відсутність розбіжностей між певними умовами і властивостями сукупності).
2. Альтернативна гіпотеза (Н1): сукупність не відповідає певним умовам.
З цих двох гіпотез вірною є лише одна. Прийнявши ту, чи іншу гіпотезу ми можемо вгадати реальну ситуацію, а можемо й помилитись.
ПРИКЛАД. РЛС військового літака, що виготовлені за традиційною технологією мають середню дальність виявлення стандартної цілі 91 км при σ = 1 км. Це означає, що із всієї сукупності штатних РЛС 99,7% з них виявляють стандартну ціль на відстані 88-94 км.
Певний виробник РЛС при застосуванні нової (більш дешевої) технології, яка теоретично не повинна була б погіршувати вказаний параметр виявив, що пробна партія нових РЛС показала середню дальність виявлення стандартної цілі 89 км. Треба визначити чи дійсно нова технологія зменшує вказану характеристику, чи просто на дослідження потрапили не найкращі зразки?
Тому мають місце дві гіпотези:
Нο: середня дальність виявлення цілі для нових РЛС така сама, як і у традиційних, просто на дослідження потрапили найгірші зразки . Прийнявши цю гіпотезу ми одночасно приймаємо рішення про перехід на нову технологію виготовлення РЛС.
Н1: нова технологія викликає зменшення дальності виявлення стандартної цілі і отримані результати вибірки не випадкові. Ця гіпотеза змушує відмовитись від переходу на нову технологію.
Описану проблему можна звести до наступного питання : прийняти чи відхилити гіпотезу Но? Прийнявши Но ми переходимо на нову технологію, відхиливши її – відмовляємось від неї. І перше і друге рішення можуть бути помилковими.
Розрізняють помилку першого роду: відхилили гіпотезу Нο, коли вона була вірною (відмовились від нової технології, яка на справді краща за попередню). Інакше кажучи перестрахувались.
І помилку другого роду: прийняли Нο в той час, коли вона була не вірною (порахували, що отримане значення 89 км має всі шанси з’явитись у любій вибірці із штатних РЛС).
| Вірна гіпотеза | Прийнята гіпотеза | |
   Но
Но
| Но | |
 Н1
Н1
| Н1 |
Ситуація, коли кожна з гіпотез може бути вірною з’являється тому, що отримана кількісна характеристика (89 км) може свідчити як на користь одної гіпотези, так і на користь іншої. І в умовах такої невизначеності все одно треба приймати рішення.
Подібні проблеми виникають часто і в стислому вигляді їх сформулював принц Гамлет: “Бути, чи не бути?” Одне з вирішень подібної дилеми підказав свого часу Чингісхан: “Краще зробити і жалкувати, ніж жалкувати, що не зробив.”
В статистиці, на відміну від Чингісхана, застосовують математичні критерії для прийняття, або відхилення тої, чи іншої гіпотези. Все, що ми маємо – це вибірковий параметр. Якби він дав значення 91 км і більше ми б однозначно перейшли на нову технологію, а от коли він не дотягує до 91 км у нас з’являються певні сумніви щодо переходу на нову технологію. І чим вибірковий параметр менший, тим наших сумнівів більше.
Для прийняття того, чи іншого рішення відштовхуються від наступного: закон розподілу кількісної статистичної характеристики (тої яку ми отримуємо при вибірковому спостереженні) повинен бути заздалегідь відомим. Нехай графічно картина виглядає наступним чином:
 |
 F(x)
F(x)
 |
88 89 90 91 92 93 94 Дальність
Для прийняття того, чи іншого рішення треба встановити однозначне правило (критерій) коли яку гіпотезу ми приймаємо. Все що ми маємо – це якесь вибіркове значення. Значить весь діапазон зони “невизначеності” треба розбити на дві зони “впливу”. Коли вибірковий параметр потрапляє у зону гіпотези Но – приймається Но. Коли в зону Н1, то і прийматись буде Н1. Якщо ми таким чином визначимось, то тоді однозначно по вибірковому значенню можна стверджувати якою з гіпотез це значення викликане. Зрозуміло що при наближенні до 91 км більше шансів має гіпотеза Но, а при віддаленні від нього в меншу сторону 88 км - Н1. І чим це віддалення більше тим більше шансів у Н1 .
Оскільки за словами Мєнделєєва: “наука починається там, де починаються виміри”, то треба якось зрозуміло визначитись з вищенаведеними формулюванням “більше шансів” з тим, щоб обраний нами поріг найбільш оптимально розбивав вказаний діапазон.
Стосовно оптимальності розглянемо дві ситуації:
- в якості порогу обрали 89 км (“зона впливу” гіпотези Но - від 89 км і більше);
- в якості порогу обрали 90 км (“зона впливу” гіпотези Но - від 90 км і більше).
Нехай вірною є гіпотеза Но.
Обравши поріг 89 км ми з ймовірністю 0,023 робимо помилку першого роду: 2,3% вибірок із штатних РЛС дають середню дальність виявлення цілі меншу за 89 км. В усіх цих випадках ми помиляємось, коли не перейдемо на нову технологію.
Обравши в якості порога 90 км ми помиляємось з ймовірністю 0,159. Оскільки майже 16% вибірок із штатних РЛС дадуть середню дальність виявлення меншу за 90 км.
Таким чином, коли вірною є гіпотеза Но ми можемо зробити лише помилку першого роду (помилково відхилити її). Збільшуючи поріг ми збільшуємо ймовірність помилки першого роду.
Нехай вірною є гіпотеза Н1.
Обравши в якості порогу 89 км ми завжди будемо приймати невірне рішення, коли вибіркове значення буде більшим за 89 км. Тобто у всіх випадках коли вибірка дасть 89-91 км ми будемо помилятись.
Обравши в якості порогу 90 км ми будемо менше помилятись – а саме тільки тоді, коли вибіркові значення потраплять в діапазон 90 – 91 км. Збільшуючи поріг ми, таким чином, одночасно зменшуємо ймовірність помилки другого роду.
Підсумовуючи вищенаведене можна стверджувати наступне: збільшуючи поріг ми збільшуємо ймовірність помилки першого роду і зменшуємо ймовірність помилки другого роду. Зменшуючи поріг ситуація змінюється на протилежну. За критерієм Чингісхана ми би завжди робили помилку першого роду і ніколи не зробили помилку другого роду.
Людина незмозі встановити де є правда.
Але вона добре розбирається де брехня.
Б. Паскаль.
Для того, щоб визначитись яку саме величину обрати в якості порогу виходять з того, що потрібно мінімізувати збитки від прийняття невірного рішення.
При помилці першого роду (помилково відмовились від дешевої технології) ми уникаємо погіршання характеристик РЛС, але одночасно конкуренти (якщо не відмовляться від даної технології) можуть поставити на ринок такі самі РЛС, тільки більш дешеві.
При помилці другого роду (помилково перейшли на нову технологію) ми погіршуємо певну характеристику РЛС. Постає питання наскільки таке погіршання є принциповим для ринку озброєнь?
Що для нас важливіше: зробити РЛС більш дешевою, чи не погіршити певні її характеристики? Іншими словами: яку помилку (першого чи другого роду) ми більше прагнемо уникнути?
Прийнявши до уваги ту шкоду, яку може заподіяти помилка першого роду визначають такий рівень її ймовірності, який вважають в певному розумінні безпечним. Наприклад, якщо нас взагалі не лякає помилка першого роду (завдання перейти на більш дешеві РЛС не є принциповим), то на ймовірність помилки першого роду не звертають увагу і поріг обирають виходячи з завдання зменшення лише помилки другого роду (для нашого прикладу це буде 91 км і в цьому випадку ми перейдемо на нову технологію лише тоді, коли вибірковий параметр буде більше 91 км).
Якщо помилкою першого роду нехтувати не можна (питання здешевлення стоїть гостро), то визначають її “безпечний” рівень, коли помилка буде майже неймовірною в конкретній ситуації. Тобто з тих чи інших міркувань визначаються, що у конкретній ситуації нас влаштовує, що ми можемо помилитись не більше як у 1 випадку зі 100, або в 1 випадку із 1000, або в 1 випадку з 1000000 … В кожній конкретній ситуації цей рівень визначається окремо і він носить назву рівня істотності критерію.
Таким чином, коли отримана вибірка потрапляє в ту зону, де ймовірність того, що таке значення викликане гіпотезою Но менша за рівень істотності, то ми відхиляємо гіпотезу Но. Ми скоріше допустимо, що наша гіпотеза невірна, ніж допустимо появи такої малоймовірної вибірки.
Визначивши рівень істотності можна розрахувати поріг (критичне значення), який дозволяє поділити область невизначеності на дві “зони впливу” для гіпотез Но і Н1 відповідно.
Статистична перевірка гіпотез відбувається у такий послідовності:
1. Формулюють нульову, та альтернативну гіпотези.
2. Вибирають статистичну характеристику, за значенням якої перевіряють правильність нульової гіпотези.
3. Визначають рівень істотності ризику першого роду і відповідне йому критичне значення статистичної характеристики.
4. За результатами вибірки визначають фактичне значення статистичної характеристики.
5. Порівнюють критичне і статистичне значення.
6. Приймають, або відхиляють нульову гіпотезу.
(Лекція 12)
Метафізика - це коли слухач нічого не розуміє,
І коли викладач розуміє не більше.
Вольтер.
Тема 6.Методи аналізу взаємозв’язків.
1. Місце статистики у дослідженні взаємозв’язку.
Будь-яке суспільне масове явище є наслідком дії певної множини причин і одночасно є причиною інших явищ. Інакше кажучи та, чи інша поведінка сукупності зумовлюється відповідними чинниками.
Дослідження впливу різних чинників на масові суспільні явища, на відміну від природних наук, має певні особливості. Для природних наук вплив різних чинників на характер розвитку того, чи іншого явища можна трактувати однозначно і перевірити експериментально. Суспільні науки такої “розкоші” позбавлені і змушені користуватися статистичним підходом. При проведенні низки економічних, або соціальних експериментів у схожих умовах результати кожного разу можуть суттєво різнитись. Це випливає з природи масових явищ – вплив певного фактора на елементи сукупності врахувати важко, оскільки одночасно ті самі елементи підпадають під дію великої кількості інших чинників, як однакової, так і протилежної дії. І питома вага дії кожного чинника на елементи сукупності різна. Тому поведінка окремих елементів сукупності буває одночасно протилежною.
ПРИКЛАД – економіка країни в цілому зростає, а окремі підприємства можуть як покращувати свої показники, так і погіршувати. Середня заробітна платня по країні може зростати, а у окремих громадян може спостерігатись, як зростання, так і зменшення, або залишатись без змін.
Ну, а загальна поведінка сукупності, як такої буде визначатись “простою більшістю” елементів: чим більше елементів сукупності проявляють “характерну поведінку” під дією певного чинника, тим більше він (чинник) впливовий. Тобто взаємний вплив явищ, або як його ще називають взаємний зв’язок проявляється лише на базі закону великих чисел.
У багатьох сукупностях спостерігається певна взаємна узгодженість між різними ознаками – тобто властивостями елементів сукупності. Причому ця узгодженість проявляється не в кожному конкретному елементі, а в їх переважній більшості.
Дослідження зв’язків між соціально-економічними явищами потребує володіння не лише методом, а ще й предметом дослідження, а тому його поділяють на етапи:
1. Якісний аналіз явища – це аналіз природи явища, що розкриває його якісну визначеність.
2. Побудова моделі зв’язку. Базується на методах зведення та середніх.
3. Інтерпретація результатів.
Взаємний зв’язок явищ пізнається шляхом вивчення причинних відносин. Причина – це той активний вплив, що формує явище – тобто змушує проявлятись (у відповідних умовах) певним чином, а не аби як. У статистиці, на відміну від фізики, не використовують перший закон Ньютона. Тут застосовується підхід Аристотеля: якщо відбуваються якісь зміни, то обов’язково повинна бути причина, яка їх викликає. Розрізняють зв’язок між показниками і між ознаками. З показниками все зрозуміло.
ПРИКЛАД – збільшується рівень безробіття – зростає рівень злочинності.
Зв’язок між ознаками розглядається через елементи сукупності. Якщо в переважній більшості.
Ознаки явищ по їх значенню на вивчення зв’язку поділяють на два класи:
Факторні (фактори) – ті, що викликають зміни інших;
Результативні (результати) – ті що змінюються під впливом факторів.
Зв’язки між різними явищами поділяють за: характером, напрямком, аналітичним виразом, щільністю.
За характером зв’язок розрізняють на:
функціональний;
стохастичний(грець. вміти вгадувати - випадковий).
При функціональному певному значенню факторної ознаки відповідає одне і тільки одне значення результативної ознаки.
ПРИКЛАД – фізичні та хімічні процеси, математичні залежності.
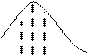
Якщо причинна залежність виявляється не в кожному окремому випадку, а в загалі при великій кількості спостережень, то такий зв’язок має назву стохастичного. Тобто одній і тій самій факторній ознаці в різних випадках відповідають різні значення результативної. Причому одні результативні значення будуть спостерігатись частіше, інші – рідше. При цьому сукупність значень результативної ознаки, що відповідає певному значенню факторної утворює умовний ряд розподілу.

 ПРИКЛАД – урожайність залежить від кількості внесених мінеральних добрив. Але чи можна точно встановити цю залежність?
ПРИКЛАД – урожайність залежить від кількості внесених мінеральних добрив. Але чи можна точно встановити цю залежність?



 Урожайність
Урожайність









 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||





 |
 Кількість внесених добрив
Кількість внесених добрив
Якщо умовний ряд розподілу замінюють одним параметром – середнім значенням по сукупності, то такий зв’язок називають кореляційним(пізньолатинське – співвідношення). Зрозуміло, що графічне зображення кореляційного зв’язку однотипне з функціональним – широка смуга замінюється лінією.
За напрямком зв’язок поділяють на:
прямий;
зворотній.
Зворотний зв’язок може бути негативним та позитивним
ПРИКЛАД –Стан економіки і рівень інвестування (позитивний). Рівновага біосистем – збільшення хижаків – зменшення травоїдних – зменшення хижаків і навпаки.
За аналітичним виразом:
лінійний;
нелінійний.
Щільність зв’язку характеризує як часто і наскільки суттєво зміна результату пов’язана зі зміною фактору. Стосовно “як часто”, це означає, що у 100% випадків, коли змінюється фактор у скількох % випадків спостерігається відповідна зміна результату? Стосовно “наскільки суттєво”, це означає, що якщо фактор варіює у всьому своєму можливому діапазоні, то в якій частині свого можливого діапазону змінюється результат?
Зрозуміло, що ставити питання про щільність функціонального зв’язку недоречно, оскільки по-перше: при ньому результат завжди (у 100% випадків) змінюється при зміні фактору і, по-друге - величина цієї зміни завжди однозначна (в певному розумінні максимально можлива).
Щільність стосується стохастичного зв’язку, коли при зміні фактору не завжди спостерігається зміна результату. І коли при значній зміні фактору зміни результату бувають як значні, так і не суттєві.
Для аналізу статистичного зв’язку використовуються наступні методи: наведення паралельних даних (паралельних рядів), аналітичного групування, дисперсійний аналіз, КРА...
2. Метод паралельних рядів.
Використовується при дослідженні розвитку явищ в часі, або просторі. Являє собою співставлення двох, або більше рядів значень статистичної ознаки. Таке співставлення дозволяє встановити зв’язок між ознаками та скласти уявлення про його характер. Може задаватись таблицею, або графіком.
| Х | |||||||||
| Y |
Залежність побудована по точках, коли в якості значень результативної ознаки використовують середні значення (кореляційний зв’язок) являє собою лінію, що має назву “ламана регресії”.
3. Метод аналітичного групування.
Основний принцип дослідження зв’язку методом аналітичного групування полягає в тому, що в якості групувальної ознаки обирають факторну. В присудку таблиці надають середні значення (абсолютні, або відносні) однієї, або більше результативних ознак. Зміна факторної ознаки при переході від однієї групи до іншої виявляє відповідні зміни результативної ознаки. Невдалий вибір інтервалів групування, або кількості груп може привести до помилок у визначенні зв’язку.
ПРИКЛАД –люба статистична таблиця.
Цей метод дозволяє лише охарактеризувати загальні риси залежності(напрямок зв’язку та уяву про форму), її тенденцію. Більш детальну інформацію метод групування не надає.
(Лекція 10)
Не того треба прагнути, щоб нас розумів кожний,
А того, щоб нас неможливо було не зрозуміти.
Вергілій.
4. Метод дисперсійного аналізу.
ПРИКЛАД – у певній країні треба встановити залежність інтенсивності захворювання (кількість хворих на 1000 населення) на хворобу А від рівня радіоактивного забруднення місцевості. Факторна ознака рівень забруднення. Результативна ознака – інтенсивності захворювання.
Країну поділили на n регіонів і дослідили (і на радіоактивність і на захворюваність). Вважають, що зв’язок між цими показниками існує тоді, коли зі зміною фактора спостерігається відповідна зміна іншої ознаки (нижчий фон – менше хворих). Але на хворобу А можуть впливати і інші чинники. Тому постає питання: якою мірою хвороба А пов’язана саме з радіоактивним фоном (і чи пов’язані вони взагалі)?
Дано: спостерігається варіація певної ознаки (інтенсивності захворювання). Треба встановити, в якій мірі вона викликана варіацією іншої ознаки (яку підозрюють за факторну). Інакше кажучи треба встановити, чи є зв’язок між цими ознаками і наскільки він сильний?
Вважається, що коли зі зміною фактора завжди спостерігається зміна результативної ознаки, то зв’язок між ними сильний. А коли фактор змінюється, а результат не змінюється, то зв’язку між ними нема. Ну і коли фактор змінюється сильно, а результат при цьому теж змінюється, але не дуже суттєво, то вважають, що між фактором і результатом існує частковий зв’язок.
Таким чином основна ідея полягає в наступному: вплив всіх інших чинників (за виключенням фактору) на результат залишити незмінним, а фактор примусити змінюватись. І спостерігати при цьому за поведінкою результативної ознаки. Якщо вона буде варіювати у всьому можливому діапазоні, то це викликано тільки варіацією фактору (бо всі інші чинники незмінні). Якщо результативна ознака незмінна, то зв’язку нема, ну а якщо результат варіює, але не в повній мірі, то зв’язок частковий. А, значить, повну варіацію результату викликають зміни інших чинників.
Коли до певної сукупності застосовують аналітичне групування, то намагаються досягти однієї мети, а саме - звузити діапазон варіації факторної ознаки у окремій групі у порівнянні з усією сукупністю і, таким чином, виключити (або суттєво зменшити) вплив варіації фактора на варіацію результату у групі. Тоді, якщо у такий групі спостерігається значна варіація результату, то зрозуміло, що викликана вона іншими причинами, а не варіацією факторної ознаки.
Нехай в результаті спостереження встановлено, що діапазон радіаційного забруднення на місцевостях, що досліджуються змінюється від Хmin до Хmax. Інтенсивність захворювання, що спостерігається у цих же місцевостях – від Ymin до Ymax.
Розіб’ємо всю сукупність із n досліджених регіонів території радіаційного забруднення на k груп, таким чином, щоб у кожну групу потрапили місцевості з несуттєвою різницею фону (чисті зони, незначний фон, слабкий фон, середній фон, середній фон … зона лиха). Зрозуміло, що кожна з цих груп якось будуть характеризуватись інтенсивністю захворювання на хворобу А. Таким чином утворені групи захворюваності (їх буде теж k ) викладемо у вигляді наступної таблиці.
Кожна група буде характеризуватись своєю чисельністю і своєю середньою захворюваністю по групі і величиною варіації.
| № з/п | Конкретні значення інтенсивності захворювання (результат y) групування за фактором радіаційного забруднення (фактор х) | Чисельність групи (gі) | Середнє групове |
| Y1 , ………………………………..Yg1 | g1 | Ỹ1 | |
| Y1 , ………………………………..Yg2 | g2 | Ỹ2 | |
| …… | ……………………………………. | …………. | ……….. |
| k | Y 1 , ..……………………………….. Y gm | gm | Ỹk |
| Всього: | n |
Якщо у кожній окремій групі спостерігаються дуже різна інтенсивність хвороби А (значна варіація захворюваності), то зрозуміло, що вона викликана чим завгодно, тільки не зміною рівня радіації (бо у кожній окремій групі рівень майже не змінний). Така ситуація свідчить про слабкий (або зовсім відсутній) зв’язок між радіацією і інтенсивністю хвороби А. Бо фон майже стабільний, а захворюваність при цьому різна.
І навпаки, якщо у кожній групі спостерігається незначна варіація результату, то це можна пояснити незначною варіацією фактора у групі (явне свідчення про наявність зв’язку).
Крім того від групи до групи збільшується фон. Якщо при цьому спостерігається збільшення середньої захворюваності по групах, то це можна пояснити якраз збільшенням фону. Тобто така залежність вказує на існування зв’язку між фактором і результатом.
Варіація, як відомо, характеризується дисперсією. Використання властивостей дисперсії дозволяє оцінити статистичний зв’язок між ознаками.
При аналітичному групуванні можна виділити три види дисперсій результативної ознаки:
Загальну для всієї сукупності (відносно середньої всієї сукупності Y¯, де Y¯- середній рівень інтенсивності захворювання на хворобу А по країні взагалі). Загальна дисперсія результативноїознаки характеризує змінністьзахворюваності піддією всіх причин, в тому числі і від інтенсивності радіоактивного забруднення (факторної ознаки).
Y¯= Σ Yi ⁄ n (n – це кількість спостережень:)
σ² = Σ (Yi - Y¯)²/n
Групову (в окремій групі відносно середньої захворюваності для певної групи. Тобто група розглядається як окрема сукупність. У окремій групі факторна ознака майже не змінюється, тому якщо спостерігається зміна (варіація) результативної ознаки, то це може бути викликано тільки іншими причинами, а не фактором. Тобто групова дисперсія характеризує змінність факторної ознаки під дією всіх причин за виключенням варіації факторної
Ỹi = Σ Yi /gi
σ²i = Σ (Yi - Ỹi )²/gi
Якщо групова дисперсія дорівнює нулю, це означає, що інші причини не змінюють результативної ознаки. Ознака не змінюється (тобто Yi = Ỹi), значить на неї ніщо не впливає.
Загальний вплив всіх інших чинників (за виключенням фактору) на варіацію результату по всій сукупності оцінюють за допомогою середньої з групових дисперсій., яка розраховується, як середня арифметична зважена. Вона є узагальнюючою мірою впливу, що характеризує вклад у загальну дисперсію всіх інших чинників за виключенням варіації факторної ознаки і враховує внесок кожної групи у цю величину. Тобто, як в середньому по всій сукупності дія всіх інших чинників впливає на варіацію результату.
σ¯² = Σ σ²i gi/ Σgi
Міжгрупову (характеризую варіацію групових середніх навколо загальної середньої). Вважається, що всі інші причини, що викликають варіацію результатів вимірювання у всіх групах однакові., і кожна група відрізняється лише рівнем радіоактивного забруднення. Тому, якщо при послідовному збільшенні значення рівня радіоактивного забруднення Хi не спостерігається змін у середньому значенні у групах інтенсивності захворювання на хворобу А (Y¯ = Ỹi) , то факторна ознака ніяк не пов’язана з результативною. Міжгрупова дисперсія може виникнути лише під впливом змінності факторної ознаки. Бо якщо змін середніх групових результату нема, то значить, що зміна факторної ознаки не впливає на зміну результативної. Тобто можна говорити про наявність, або відсутність певного зв’язку між ознаками (зв’язок – це коли одна зміна супроводжується іншою зміною).
δ² = Σ (Ỹi - Y¯ )² gi / Σgi
Відомий закон, що пов’язує ці види дисперсій. Логіка цього закону проста: загальна дисперсія, що виникає під дією всіх факторів дорівнює сумі дисперсій, що визначаються і фактором (δ²), і всіма іншими чинниками (σ¯²).
σ² = σ¯² + δ²
На підставі цих видів дисперсії вводять кореляційне відношення:
η² = δ²/ σ²
Тобто визначають яку частку у загальній дисперсії становить міжгрупова.
Інакше кажучи, визначають скільки відсотків загальної варіації обумовлено фактором, що покладений у основу групування, а скільки іншими чинниками. Кореляційне відношення змінюється від 0 (фактор не впливає на результат) до 1 (вплив інших чинників відсутній). Форма залежності ознак (лінійна, нелінійна) залишається невідомою.
Я кажу вам своє остаточне: “може бути”
Г. Спенсер.
5. Перевірка істотності зв’язку.
Може статися така ситуація, коли випадково розподіл результативної ознаки по групах відбувся так, ніби, зв’язок є, коли насправді його нема. Або навпаки зв’язку нема, а групові середні величини випадково виявили тенденцію зростання. Бо всі дослідження базуються на емпіричних даних, а тому кожна конкретна ситуація не обов’язково буде співпадати з загальною закономірністю масового явища. Від таких випадків ніхто не застрахований і тому треба якось враховувати цю випадкову можливість прийняття невірного рішення. Цю проблему досліджував Р. Фішер і встановив, що чим більша загальна сукупність і чим на більше число груп ми її розбиваємо, тим достовірніший отримуємо результат (прояв закону великих чисел). Р. Фішер запропонував критерії, за допомогою яких можна встановити ймовірність того, що між ознаками дійсно є статистичний зв’язок, коли розрахунки на нього вказують. Їх два: критерій Фішера, та F – критерій.
1. Критерій Фішера:
Визначають ступені свободи k1 = m-1 і k2 = n-m (n – чисельність сукупності, m – кількість груп). А далі користуються таблицями критичних значень η²кр, що відповідають певному рівню істотності (тобто Р. Фішер знайшов ті значення η², які могли б виникнути випадково без наявності зв’язку). Якщо розраховане значення перевищує критичне, то вважається, що зв’язок між ознаками дійсно існує. Рівнем істотності щодо висновків про наявність зв’язку задаються наперед і потім по відповідних таблицях Фішера визначають η²кр.
Як і всі інші оцінки у статистиці, істотність гарантується не 100%, а з певною ймовірністю. Ця ймовірність задається рівнем істотності. Наприклад рівень істотності зв’язку α = 0,05 означає, що у 5 випадках із 100 при дійсній наявності статистичного зв’язку між ознаками розраховане значення η² не перевищує η²кр (ризик першого роду).І, відповідно у 5 випадках зі 100 при відсутності зв’язку η² перевищує η²кр (ризик другого роду). Тобто підхід, розроблений Фішером, дозволяє задаватись ймовірністю того, що ми можемо помилитись, визначаючи щільність зв’язку методом дисперсійного аналізу.
2.Аналогічно використовують F – критерій:
F = η² k2 ⁄(1- η² ) k1.
Розраховане значення F порівнюють з критичним значенням F кр. Обидва критерії дають ідентичні оцінки, оскільки F і η² функціонально пов’язані. F – критерій застосовують у тих випадках, коли ступені свободи приймають великі значення, бо його таблиці критичних значень менш громіздкі.
(Лекція 11)
Факти – це пісок, що скрежетить
В шестернях ясної теорії.
С. Гарцинський.
6. Метод кореляційно-регресійного аналізу.
Не завжди буває можливо розбити певну сукупність на групи так, щоб у кожній групі факторна ознака майже не варіювала. В таких випадках щільність зв’язку визначають за допомогою метода кореляційно-регресійного аналізу. Вихідною інформацією при цьому виступає , так звана, ламана регресії – ламана лінія, яка графічно відбиває залежність: фактор – середнє значення результату. Ця лінія будується на підставі емпіричних даних (тобто отриманих на підставі реального дослідження).
ПРИКЛАД – у певній країні по всіх регіонах досліджується залежність між кількістю автомобілів і кількістю ДТП за рік на 1000 населення .
 |
0,7








 0,6
0,6
 |




 0,5
0,5
 |


 0,4
0,4
 |

 0,3
0,3
 |
60 70 80 90 100 110 120 130
Основна ідея зводиться до наступного: коли ламана регресії на значних ділянках приймає вигляд, що дуже нагадує певну математичну функцію, то вважається, що є підстави моделювати (принаймні на цих ділянках) залежність між фактором і результатом відповідною теоретичною функцією. Таке припущення дозволяє зробити відповідну апроксимацію. Підібний підхід виправдовується тим, що у багатьох різних за своєю природою явищах, залежність між ознаками дійсно описується однаковими кількісними співвідношеннями. Це якраз та властивість навколишнього світу, яка свого часу привела Піфагора до висновку, що основою гармонії всесвіту є кількісні співвідношення. У своїх відомих “золотих віршах” давньогрецький вчений стверджував, що “природа світу цього однорідна”.
Аналітичне моделювання залежності ФАКТОР-РЕЗУЛЬТАТ має назву рівняння регресії., що задає певну теоретичну лінію регресії (на графіку зображена пунктиром).
Рівняння регресії Y= f(x) – це аналітична модель реальної залежності між ознаками, яка дозволяє абстрагуватись від множини додаткових чинників, що теж впливають на реальну величину результативної ознаки. В деяких випадках рівняння регресії має за мету штучно спростити характер цієї залежності, а тому відбиває його більш – менш правдоподібно. Інакше кажучи при такому підході вважається, що дійсна залежність між фактором і результатом відповідає певній математичній функції і тільки вплив різних додаткових чинників спотворює цю гармонію і замість красивої математичної функції ми змушені задовольнятись ламаною регресії.
Зрозуміло, що якщо залежність між ознаками можна навести у вигляді функції Y= f(x), то це означає, що значення результату (Y) залежить лише від величини фактора (x) і більше не від чого (100% залежність). Бо знаючи х ми на 100 % можемо гарантувати, що величина Y при цьому буде Y= f(x).
Вплив різних додаткових чинників викликає відхилення емпіричних даних (y) від теоретичної кривої (Y). Відхилення емпіричних даних від теоретичної лінії е = (y – Y) називають залишками.
Y – це теоретичний (очікуваний) рівень результативної ознаки. (на графіках показано пунктиром). Зрозуміло, якщо отриманий емпіричний результат не співпадає з очікуваним, то це вказує на те, що результативна ознака залежить не тільки від факторної, але ще й від інших додаткових чинників. І чим залишки більші, тим вплив додаткових чинників на результат більш суттєвий, тобто тим менше залежить результат безпосередньо від фактору (тим менша між ними щільність зв’язку).
У статистиці використовують різні математичні види рівняння регресії, що моделюють різні види зв’язку:
- лінійне Y = a + bx;
- степеневе Y = aх³;
- гіперболічне Y = a + b/x;
- параболічне Y = a + bx + сх²;
- логарифмічне Y = loga х
ПРИКЛАД –залежність між урожайністю і кількістю внесених добрив, залежність собівартості продукції від обсягу її виробництва.
Якщо кривизна ламаної регресії невелика, то використовують лінійну залежність: Y = a + bx; а – вільний член рівняння регресії ( у при х = 0), b – коефіцієнт регресії і розглядається, як ефект впливу. Вибір параметрів рівняння регресії здійснюється на підставі методу найменших квадратів.
Σ (y – Y)² = min;
Це дозволяє забезпечити, в певному розумінні, мінімальні розбіжності між емпіричною і теоретичною лініями регресії на всьому діапазоні спостережень.
Математично доведено, як на підставі одержаних емпіричних даних(у1, у2, у3, …) отримати коефіцієнти лінійного рівняння (a, b) такі, щоб вони відповідали умові найменших квадратів.
Вимір щільності зв’язку у методі КРА грунтується на припущенні, що при повній незалежності ознак Х і Y відхилення результату Y від свого середнього рівня (за знаком і за величиною) ніяк не пов’язані з відповідними відхиленням фактору Х від свого середнього рівня.
Графічну залежність між фактором і результатом при незалежності ознак відобразити неможливо. І навпаки, при наявності сильної залежності (тобто тільки від фактору) зміна фактору завжди приведе до однозначного характеру зміни результату. А це вже можна відобразити графічно. Обидві картини кореляційного поля надано на малюнках, які наводять залежність між зростом і доходом (нема зв’язку), та зростом і масою (прямий зв’язок) для однієї і тієї ж самої сукупності людей.
 | |||
 | |||

 Маса Дохід
Маса Дохід
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
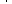 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  | ||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
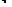 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
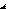 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
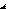 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
Зріст Зріст
Оскільки завжди, коли тільки можливо люди намагаються йти шляхом найменшого опору, то і при дослідженні залежності між ознаками в переважній більшості випадків зв’язок між ознаками намагаються моделювати лінійною залежністю. Навіть якщо загальна залежність нелінійна, на окремих ділянках її можна вважати лінійною. Вимір щільності зв’язку при лінійній залежності між ознаками здійснюють за допомогою коефіцієнта кореляції К. Пірсона. Основна ідея полягає у тому, що при наявності лінійного зв’язку і його відсутності змінюється загальна картина кореляційного поля – або спостерігається скупчення значень навколо певної лінії, або загальна картина розмазується.
Відхилення факторної ознаки х в ту, чи іншу сторону від свого середнього значення по сукупності і відповідні їм відхилення результативної ознаки Y мають знаки + і -. Δх= х- х¯, Δу = у- у¯. Знак добутку Δх Δу залежить від напрямку відповідних відхилень ознак.
 | |||||||
 | |||||||
|
| ||||||
Y¯
 | |||
 |
Х¯
А сума всіх можливих добутків Σ (Δх Δу) буде зростати тим сильніше, чим краще виконуються дві наступні умови:
- більше узгодженості у взаємних відхиленнях фактор-результат за знаком;
- більше узгодженості взаємних відхилень за величиною .
 Гранична сума цих добутків дорівнює: Ö Σ Δ²х Σ Δ²y
Гранична сума цих добутків дорівнює: Ö Σ Δ²х Σ Δ²y
Коефіцієнт кореляції визначається відношенням зазначених сум:
 r = Σ (Δх Δу) / Ö Σ Δ²х Σ Δ²y
r = Σ (Δх Δу) / Ö Σ Δ²х Σ Δ²y
Коефіцієнт кореляції, оцінюючи щільність зв’язку, вказує також його напрямок (прямий чи зворотній). Він характеризує інтенсивність лінійного зв’язку. Змінюється від –1 до +1. Оцінюється щільність зв’язку за такими критеріями:
| Ступінь | Величина r |
| Сильний | 1,0 – 0,7 |
| Середній | 0,7 – 0,3 |
| Слабкий | 0,3-0,1 |
Частіше за все при дослідженнях використовують наступну формулу для розрахунку коефіцієнта лінійної кореляції:


 r =(х у – х * у ) ∕ σх σу
r =(х у – х * у ) ∕ σх σу
Коефіцієнт кореляції функціонально пов’язаний з коефіцієнтом регресії:
r = bσх/σу
Коли зв’язок між ознаками нелінійний, то коефіцієнт кореляції не надає коректної інформації про щільність звязку, оскільки при нелінійній залежності внески всіх Δу у коефіцієнт кореляції нерівнозначні. При пропорційній зміні Δх спостерігається непропорційна зміна Δу, що порушує другу умову зростання суми добутків.
Важливою характеристикою взаємозв’язку ознак є відносний ефект впливу фактора х на результат у. Він має назву коефіцієнта еластичності:
γ = bх¯/ у¯
Він показує на скільки % у середньому змінюється у зі зміною х на 1%.
Універсальною мірою щільності звязку між ознаками при всіх видах залежності в методі КРА є коефіцієнт детермінації R, який знаходять на підставі трьох наступних видів дисперсії результативної ознаки: загальноїσ²у, що характеризує середнє відхилення від середнього значення по сукупності дисперсію, факторної δ²., що характеризує умовні (теоретичні) відхилення від середнього рівня і залишкової σ²е, що характеризує середні відхилення між фактичними даними і теоретичними припущеннями результативної ознаки. Для наведеного вище прикладу:
- загальна дисперсія σ²у це параметр, який показує, як в середньому відрізняються фактичні рівні ДТП у різних регіонах країни від середнього рівня ДТП по країні;
- факторна дисперсія δ² характеризує як би в середньому рівень ДТП у різних регіонах країни відрізнявся від середнього рівня ДТП по країні, якби залежність між фактором і результатом відповідала певному рівнянню регресі. Зрозуміло, що скільки різних рівнянь регресії ми оберемо для моделювання залежності, стільки і різних факторних дисперсій отримуємо.
- залишкова дисперсія σ²е характеризує, яка в середньому буде розбіжність між ламаною регресії і рівнянням регресії.
Ці всі дисперсії пов’язані наступним чином:
σ²у = δ² + σ²е
Факторна дисперсія характеризує відхилення теоретичної лінії регресії від середнього значення. Залишкова характеризує середню розбіжність між емпіричними даними і прийнятою теоретичною моделлю. Зрозуміло, що коли емпіричні дані дуже добре “вписуються” в теоретичну лінію регресії, то залишкова дисперсія мінімальна, а факторна майже дорівнює загальній. Знаючи величину фактору можна точно визначити значення результату, а значить результат залежить лише від фактору (сильний зв’язок).
І навпаки, коли теоретичний графік не “вписується” в емпіричні дані, то зростає доля залишкової дисперсії. Це означає, що теоретична крива не дуже “вдало” буде демонструвати залежність фактор-результат. Знаючи величину фактору важко визначитись з середньою величиною результату (зв’язок слабий). Потрібно враховувати ще якісь чинники.
Аналогічно до ДА розглядають коефіцієнт детермінації (і індекс кореляції):
R² = δ²/ σ²у
За відомим лінійним коефіцієнтом кореляції також можна визначити якою мірою варіація результату визначається варіацією фактору. Цей відсоток становить r².
R² = r².
Оскільки коефіцієнт детермінації, як і кореляційне відношення залежить від емпіричних (тобто випадкових) даних, то потрібно визначити істотність отриманих оцінок.
Робиться це порівнянням розрахованих оцінок з критичними. Тобто такими, що могли б виникнути за відсутністю зв’язку. Якщо фактичне значення перевищує критичне, то зв’язок не випадковий.
Для кореляційного відношення і коефіцієнта детермінації використовують критерій Фішера. Для визначення критичного значення він враховує:
- m кількість груп (параметрів рівняння регресії);
- n загальний обсяг сукупності;
- ступінь свободи фактора К = m-1;
- ступінь свободи випадкової дисперсії К = n-m.
Таблиця критичних значень Фішера розроблена для різних значень ймовірності ризику першого роду і дозволяє з певною ймовірністю стверджувати, що тільки у 1, 2, 5 або 10 випадках зі 100 при дійсному існуванні зв’язку між ознаками може випадково виникнути кореляційне відношення, яке не перевищує критичне значення.
При перевірці істотності зв’язку частіше використовують F – критерій Фішера. При великих значеннях ступенів свободи його критичні значення мало змінюються і таблиці менш громіздкі. В якості статистичної характеристики F – критерію Фішера використовують дисперсійне відношення. Між характеристиками є функціональний зв’язок, а тому результати перевірки будуть ідентичні.
R² k2
 F =
F =
(1 – R²) k1
(Лекція 12)
Життя створює порядок,
Але порядок не створює життя.
А. С. Екзюпері.
7. Оцінка узгодженості варіації атрибутивних ознак.
Соціальні явища характеризуються не тільки кількісними, але і якісними ознаками, які не можна порівнювати за величиною. Варіанти якісних ознак просто фіксуються.
ПРИКЛАД – населення характеризується різними якісними ознаками: рівнем освіти, національністю, професіями, соціальним статусом, статтю… Підприємства характеризуються: формою власності, приналежністю до певної галузі, видами діяльності…
Виявляється, що зв’язок може існувати і між якісними ознаками. При цьому не спостерігається узгоджена зміна величини ознаки (зростає фактор – зростає і результат), бо якісні ознаки не зростають і не зменшуються. Вони просто стрибком змінюються. Але при цьому може спостерігатись наступна закономірність – певне значення однієї ознаки переважно зустрічаються тільки з конкретним значенням іншої. Ніби між ціми варіантами ознак існує більш, або менш виражене взаємне тяжіння.
При кількісних ознаках таке “тяжіння” призводить до узгодженої зміни середніх рівнів фактору і результату. При якісних ознаках відбувається своєрідний перерозподіл елементів в самій сукупності.
ПРИКЛАД – досліджується певний колектив (100 осіб) стосовно двох ознак: національність і освіта. Картина може бути двох принципово різних видів:
| Національність | Освіта | Разом | |||
| Середня | Вища | Наукова ступінь | |||
| Українці | |||||
| Росіяни | |||||
| Вірмени | |||||
| Євреї | |||||
| Разом |
| Освіта | Разом | ||||
| Середня | Вища | Наукова ступінь | |||
| Українці | |||||
| Росіяни | |||||
| Вірмени | |||||
| Євреї | |||||
| Разом |
Кожна ознака розбиває сукупність на відповідні групи. Ознаку, що вважаємо за фактор розташуємо у підметі таблиці. Таблиці, в яких наведений розподіл сукупності по атрибутивним ознакам називаються таблицями співзалежності (ТС).
Різниця у цих таблицях криється у характері розподілу сукупності – підсумкові значення в обох таблицях однакові, а фактичні розрізняються. Ця різниця може бути більшою, або меншою.
Якщо українців у загальному колективі 40% і одночасно їх 40% серед людей з середньою освітою, і 40% серед людей з вищою освітою, і 40% серед людей з науковим ступенем, то це означає, що українці мають однакову питому вагу у кожній групі, що відповідає певному значенню освіти. Тобто українці не тяготіють до якогось окремого рівня освіти. Такий розподіл має назву пропорційного.
Якщо ж спостерігається, що в той час, коли українців у колективі 40%, а серед людей з середньою освітою їх 43%, а серед людей з науковим ступенем їх тільки 20%, то це означає, що українці намагаються освітою себе не обтяжувати. Ця національність “тяжіє” до середньої освіти. Зрозуміло, що коли українці займуть непропорційно багато місця в середній освіті, то це означає, що вони тим самим звільняють місця для інших національностей наприклад у вищій освіті. Тоді якась інша національність буде “тяжіти” більшого рівня освіти. І чим сильніше виражене це “національне тяжіння”, цей дисбаланс, тим зв’язок між ознаками вважається більш сильним. В наведеному прикладі це означає, що серед вчених ми маємо більше шансів натрапити на єврея, ніж на українця, а серед селян навпаки. Якщо різні національності по різному концентруються в наведених “освітніх” групах, то ця різниця чимось викликається – тобто є зв’язок між ознаками.
Щоб встановити наскільки цей зв’язок суттєвий вимірюють вищевказаний дисбаланс між ознаками. Вимір цього дисбалансу полягає у інтегруванні (накопиченні) відхилень фактичних частот в розподілі сукупності і пропорційних частот..
Якби рівень освіти не залежав від національності, то розподіл був би пропорційним:
Fij = fio fio /n
fio, fio – підсумкові частоти за відповідними ознаками.
Коли ж така залежність є , то фактичні частоти fij якось відрізняються від пропорційних fij ≠ Fij. І чим сильніша ця відмінність тим цей зв’язок суттєвіший.
Загальною характеристикою абсолютних відхилень фактичних частот від пропорційних є так званий критерій хі-квадрат Пірсона.
χ² = ΣΣ(fij – Fij) ²/F²ij =n[ΣΣ f²ij / fio fio ]
За відсутності стохастичного зв’язку χ² =0.
Читайте також:
- Наприклад.
- Наприклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
| <== попередня сторінка | | | наступна сторінка ==> |
| Середня величина. | | | НОРМАТИВНО-ПРАВОВІ АКТИ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |