• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рушійна сила масообмінних процесів

Рушійна сила масообмінних процесів визначається ступінню відхилення від рівноваги або "відстанню" від рівноваги. Останнє зумовлює різницю між робочою і рівноважною концентрацією або рівноважною і робочою, в залежності від того, які з них більші. При цьому очевидно, що рушійну силу можна виразити або через концентрації розподіляючої речовини в фазі G, тобто через У, або через концентрації його в фазі L, тобто через X.

На (Рис. 7.5.1.) показані можливі варіанти виразу рушійної сили масообмін них процесів
при різних напрямах переходу розподіляючої речовини.

Відповідно основне рівняння масопередачі можна записати у вигляді

dM = K_y·AY·dF (8.5.1)

або

dM=K_x·ΔX - dF (8.5.2)

Індекси біля К показують, які концентрації прийняті для виразу рушійної сили. В загальному випадку

ΔY ≠ ΔХ і К_y ≠ К_x,але, очевидно, завжди

K_y ·ΔY = K_x·ΔX (8.5.3)

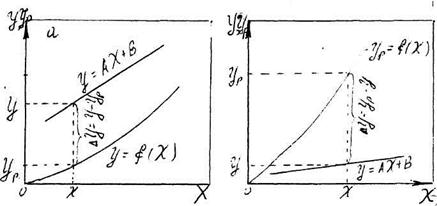
Як видно з (Рис.8.5.1), рушійна сила змінюється зі зміною робочих концентрацій, тому для всього процесу масообміну, що проходить в межах зміни концентрацій від початкових до кінцевих, повинна бути визначена середня рушійна сила(ΔΥ_m і ΔХ_т).

З урахуванням середньої рушійної сили процесу, основне рівняння масопередачі для всієї поверхні контакту фаз може бути записане у вигляді

M = K_yΔY_mF (8.5.4)

або

M = K_xΔX_mF (8.5.5)

При визначенні середньої рушійної сили можуть зустрітися два випадки:

1) залежність між рівноважними концентраціями не лінійна; для цього випадку
рівноважна концентрація визначається загальною функціональною залежністю

Y_P =f(X)

2) залежність між рівноважними концентраціями лінійна, тобто Y_р = А_р X
(де А - постійна величина).

Спочатку знайдемо середню рушійну силу для випадку Y_р =f(X)

Розглянемо зміну концентрацій X та У вздовж поверхні розподілу фаз при їх взаємодії. Для випадку Y>Y_Р при взаємодії паралельних потоків фаз поздовж поверхні розподілу Y зменшується, а X зростає (рис.8.5.2). Кожній концентрації X, згідно рівняння У_р = f(X) , відповідає рівноважна концентрація Y_р. Для елемента поверхні dF рушійна сила процесу може бути виражена різницею Y-Y_р.

Для елемента поверхні dF маємо:

dM = К_у(Y-Y_p) dF; dM = G(-dY).

Співставимо ці рівняння і отримаємо:

DF = -G/K_y* dY/(Y-Y_p)

Після інтегрування в межах 0- F і Y- Y_р маємо:

Замінивши з рівняння (7.4.2) G = M/(Y-Y_P), знайдемо:

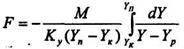(8.5.6)

або 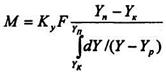(8.5.7)

Виражаючи рушійну силу через концентрації, аналогічно попередньому отримаємо:

(8.5.8)

Порівнявши рівняння (8.5.7) і (8.5.8) з рівняннями (8.5.4) і (8.5.5.), знайдемо наступні вирази середньої рушійної сили:

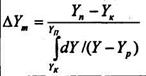(8.5.9)

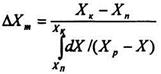(8.5.10)

Подібна структура рівнянь зберігається і в тих випадках, коли замість концентрацій використовують інші параметри, що характеризують систему: ентальпію, хімічний потенціал.

Рис.8.5.2. До визначення середньої рушійної сили дифузійних процесів.

Рис.8.5.3. До визначення середньої рушійної сили процесів графічним інтегруванням.

Рівняння (8.5.9.) і (8.5.10.) вирішують аналогічно, графічним або численним інтегруванням. Так при графічному інтегруванні знаменника дробу в рівнянні (7.5.9.) в межах концентрації Y_K - Y_n через певні інтервали для ряду значень У знаходять* відповідні їм значення X, У_р, Y- Y_р і 1/(Y- Y_p)

Потім на діаграмі в координатах Y, 1/(Y- Y_p) будують криву, як показано на рис.7.5.3. Площа під кривою обмежена ординатами У_к / У_П помножена на масштаб діаграми Syа, дає шуканий інтеграл (8.5.11.). У випадку вираження рушійної сили через концентрацію X аналогічним шляхом визначають S_xa (8.5.12.):

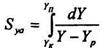(8.5.11);

(8.5.12).

Інтеграли, які знаходяться в правій частині рівнянь (7.5.11.) і (7.5.12.), широко використовуються при розрахунку масообмінної апаратури; їх позначають через т_у і m_x називають числами одиниць переносу:

(8.5.13)

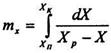(8.5.14)

Число одиниць переносу має фізичну суть, яка характеризує зміну робочої концентрації фази, що переноситься на одиницю рушійної сили.

Число одиниць переносу визначають по середній рушійній силі. З співвідношення (7.5.9.),(7.5.13.), (7.5.10.) і (7.5.14.) випливає:

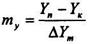(8.5.15)

(8.5.16)

Співвідношення (7.5.13) і (7.5.14) справедливі для випадку коли між робочими і рівноважними концентраціями існує залежність - як нелінійна, так і лінійна.

Для лінійної залежності, для умов Y=AХ і Y=А_РХ число одиниць переносу визначають наступним чином

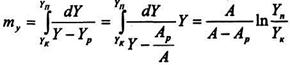(8.5.17)

(8.5.18)

Читайте також:

1. Автоматизація виробничих процесів
2. Безпечність виробничих процесів
3. Взаємодія процесів
4. Взаємозв’язок фінансових потоків та інфляційних процесів
5. Взаємозв’язок фінансових потоків та інфляційних процесів
6. Види соціальних процесів.
7. Використання особливостей протікання відновних процесів при побудові спортивного тренування
8. Використання процесів псевдозрідження
9. Вимоги IDEF3 до опису процесів бізнесу
10. Вимоги безпеки до виробничих процесів та обладнання.
11. Відображення і моделювання процесів
12. Вплив глобалізаційних процесів на культуру сучасного світу.

Переглядів: 3050