
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклад реалізації протоколу Шаміра
Побудова відомої порогової схеми Аді Шаміра базується на поліноміальній інтерполяції і на тому факті, що одномірний поліном степені над полем Галуа унікально задається по точках. Поліноми можуть бути задані над -ічним розширеним полем. При цьому коефіцієнти полінома задаються над полем як елементи поля . Основними параметрами такої схеми є числа , де – мінімальне число частин секрету, з використанням яких може бути відновлений загальний секрет, а – загальне число часток секрету, причому, .
Коефіцієнти 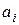 визначаються чи задаються числом
визначаються чи задаються числом 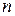 часток секрету. Потім випадковим чином формується загальний секрет
часток секрету. Потім випадковим чином формується загальний секрет 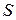 , що має бути розділений на частки секрету
, що має бути розділений на частки секрету 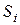 ,
, 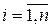 . Пропонована схема має бути такою, щоб будь-які
. Пропонована схема має бути такою, щоб будь-які 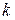 об'єктів чи суб'єктів, об'єднавши свої
об'єктів чи суб'єктів, об'єднавши свої 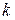 приватних секретів могли однозначно відновити загальний секрет
приватних секретів могли однозначно відновити загальний секрет 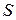 . При цьому всі частки секрету
. При цьому всі частки секрету 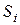 є конфіденційними, і протягом їхнього життєвого циклу мають бути забезпечені цілісність, дійсність, конфіденційність і приступність.
є конфіденційними, і протягом їхнього життєвого циклу мають бути забезпечені цілісність, дійсність, конфіденційність і приступність.
При виконанні наведених вище вимог і умов порогова схема поділу секрету А. Шаміра реалізується в такий спосіб:
1.Формується велике просте число 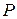 , що реально більше припустимого
, що реально більше припустимого 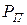 , тобто
, тобто
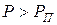 .
.
2.Формується випадковим чином загальний секрет 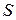 , що є елементом поля
, що є елементом поля  , тобто ціле
, тобто ціле 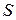 задовольняє умову:
задовольняє умову:
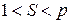 .
.
3. Випадково формується 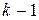 коефіцієнтів полінома
коефіцієнтів полінома 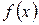 –
–  , що оголошуються конфіденційними.
, що оголошуються конфіденційними.
4. Як 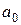 приймається значення загального секрету
приймається значення загального секрету 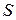 , тобто
, тобто 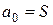 .
.
5. Довірена сторона розділяє загальний секрет, обчисливши частки секрету 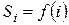 , де
, де 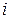 – числовий ідентифікатор або номер кожного з об'єктів чи суб'єктів, причому,
– числовий ідентифікатор або номер кожного з об'єктів чи суб'єктів, причому,  . Розподіл секрету може полягати в присвоєнні кожному з об'єктів чи суб'єктів унікального випадкового ідентифікатора.
. Розподіл секрету може полягати в присвоєнні кожному з об'єктів чи суб'єктів унікального випадкового ідентифікатора.
6.Усі частки секрету 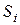 транспортуються і установлюються чи вкладаються кожному з об'єктів чи суб'єктів із забезпеченням конфіденційності, дійсності, цілісності, приступності і спостережливості.
транспортуються і установлюються чи вкладаються кожному з об'єктів чи суб'єктів із забезпеченням конфіденційності, дійсності, цілісності, приступності і спостережливості.
Надалі ми розглянемо окремо алгоритм контролю дійсності кожної з частин секрету.
Відновлення загального секрету виробляється на основі використання не менш 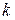 цілісних і справжніх часток секрету, чи
цілісних і справжніх часток секрету, чи 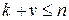 часток секретів, не більш ніж
часток секретів, не більш ніж 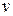 з яких можуть бути сформовані об'єктом чи суб'єктом зловмисником чи перекручені. Ці
з яких можуть бути сформовані об'єктом чи суб'єктом зловмисником чи перекручені. Ці 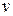 і менш приватних секретів з порушеною цілісністю виявляються і не враховуються при виробленні загального секрету. Відновлення загального секрету виконується в такому порядку:
і менш приватних секретів з порушеною цілісністю виявляються і не враховуються при виробленні загального секрету. Відновлення загального секрету виконується в такому порядку:
1. Кожний з об'єктів(суб'єктів) передає і/чи встановлює приватний секрет 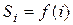 у довірений пристрій вироблення загального секрету з забезпеченням конфіденційності, цілісності і дійсності.
у довірений пристрій вироблення загального секрету з забезпеченням конфіденційності, цілісності і дійсності.
2. Довірений пристрій контролює цілісність і дійсність приватних секретів, якщо ця функція реалізована в схемі поділу секрету, а потім вибирає з них 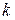 справжніх.
справжніх.
3. За 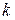 значенням
значенням  в довіреному пристрої виробляється відновлення
в довіреному пристрої виробляється відновлення 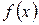 з використанням інтерполяційної формули Лагранжа:
з використанням інтерполяційної формули Лагранжа:
 . (2.144)
. (2.144)
4. Загальний секрет формується у вигляді
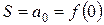 .
.
Надалі 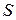 може використовуватися як ключ, пароль, загальний секрет та ін.
може використовуватися як ключ, пароль, загальний секрет та ін.
Таким чином, вироблення загального секрету в довіреному (виконуючому) пристрої виробляється на основі відновлення полінома 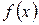 , тобто обчислення вектора коефіцієнтів
, тобто обчислення вектора коефіцієнтів  , а потім визначення загального секрету як
, а потім визначення загального секрету як 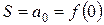 .
.
Проведений аналіз показує, що властивості граничної схеми поділу секрету Аді-Шаміра дозволяють побудувати протокол з нульовими знаннями. При відповідному виборі параметрів знання 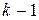 значення
значення  не дає ніякої інформації про загальний секрет. Його стійкість базується на інтерполяційній формулі Лагранжа, а також залежить від довжини модуля перетворень
не дає ніякої інформації про загальний секрет. Його стійкість базується на інтерполяційній формулі Лагранжа, а також залежить від довжини модуля перетворень 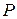 і довжин
і довжин 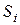 -х часток секрету. Розглянемо можливі атаки на схему Шаміра. Основною задачею атак є визначення загального секрету
-х часток секрету. Розглянемо можливі атаки на схему Шаміра. Основною задачею атак є визначення загального секрету 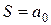 . Значення
. Значення 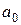 можна визначити безпосередньо або через визначення значень приватних секретів
можна визначити безпосередньо або через визначення значень приватних секретів 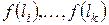 . Якщо
. Якщо 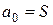 і формується довіреною стороною випадково, то складність атаки типу "груба сила" за визначенням
і формується довіреною стороною випадково, то складність атаки типу "груба сила" за визначенням 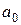 можна оцінити через імовірність
можна оцінити через імовірність 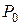 її здійснення
її здійснення
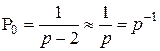 . (2.145)
. (2.145)
Складність атаки "груба сила" за визначенням 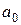 через значення
через значення  можна оцінити як
можна оцінити як
 . (2.146)
. (2.146)
Попередні порівняння (2.145) і (2.146) показують, що більш краща є атака за безпосереднім визначенням 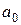 . Складність цієї атаки залежить тільки від величини модуля
. Складність цієї атаки залежить тільки від величини модуля  . Якщо
. Якщо  – відкритий загальносистемний параметр, відомий криптоаналітику, то складність атаки можна визначити також через безпечний час
– відкритий загальносистемний параметр, відомий криптоаналітику, то складність атаки можна визначити також через безпечний час
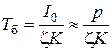 , (2.147)
, (2.147)
де 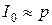 – число спроб підбору значення
– число спроб підбору значення 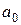 з імовірністю 1;
з імовірністю 1; 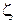 – продуктивність криптоаналітичної системи;
– продуктивність криптоаналітичної системи; 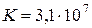 с/рік - кількість секунд у році. При цій умові
с/рік - кількість секунд у році. При цій умові 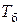 виміряється в роках. Якщо
виміряється в роках. Якщо 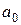 має бути визначене з імовірністю
має бути визначене з імовірністю 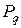 , то
, то 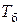 з такою імовірністю визначається із співвідношення
з такою імовірністю визначається із співвідношення
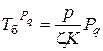 . (2.148)
. (2.148)
У табл. 2.26 наведені значення  і
і 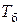 при
при 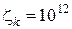 і
і 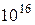 вар/с
вар/с
(у знаменнику).
Складність відновлення загального секрету схеми Аді – Шаміра.
Таблиця 2.26 – Значення  і
і 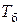 при
при 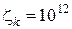 і
і 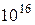 вар/с
вар/с

|  264 264
| 2128 | 2256 | 2512 | 21024 |
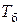 (лет) (лет)

| 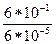
| 
| 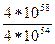
| 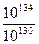
| 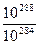
|
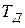 (лет) (лет)
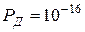
| 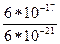
| 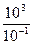
| 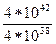
| 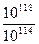
| 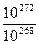
|
Аналіз даної таблиці показує, що застосування значення 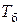 для криптографічних перетворень досягаються вже при величині модуля
для криптографічних перетворень досягаються вже при величині модуля  порядку 2256. Так, з таблиці випливає, що при довжині модуля
порядку 2256. Так, з таблиці випливає, що при довжині модуля 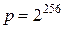 імовірність, з якою може бути здійснений криптоаналіз з
імовірність, з якою може бути здійснений криптоаналіз з 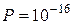 і продуктивністю криптоаналітичної системи 1016, безпечний час складає не менш 1038 років. Тому в перспективних схемах розподілу секрету величини модулів
і продуктивністю криптоаналітичної системи 1016, безпечний час складає не менш 1038 років. Тому в перспективних схемах розподілу секрету величини модулів  мають складати порядку 2256 ÷ 2512.
мають складати порядку 2256 ÷ 2512.
Основними властивостями порогової схеми Аді-Шаміра є такі:
1.Бездоганність. При знанні будь-яких 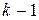 і менших часток секрету
і менших часток секрету  всі значення загального секрету
всі значення загального секрету 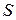 залишаються рівно імовірними і теоретично можуть вибиратися з інтервалу
залишаються рівно імовірними і теоретично можуть вибиратися з інтервалу 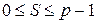 .
.
2.Відсутність недоведених допущень. На відміну від ймовірнісно-стійких схем схема А. Шаміра не базується ні на яких недоведених допущеннях (наприклад, складності вирішення таких задач як факторизація модуля, перебування дискретного логарифма і т.д.).
3.Розширювання з появою нових користувачів. Ця властивість полягає в тому, що нові частини секрету можуть бути обчислені і розподілені без впливу на вже існуючі частини.
4.Ідеальність, під якою розуміється той факт, що всі частини загального секрету і сам загальний секрет мають однаковий розмір і можуть приймати значення над полем  з рівною імовірністю.
з рівною імовірністю.
Особливістю граничної схеми розподілу секрету є те, що вона вимагає виконання модульних операцій над великим полем  , складність яких має поліноміальний характер. Крім того довірений пристрій повинний мати можливість контролювати цілісність і дійсність частин секрету перед виробленням загального секрету.
, складність яких має поліноміальний характер. Крім того довірений пристрій повинний мати можливість контролювати цілісність і дійсність частин секрету перед виробленням загального секрету.
Розподіл таємниці в системі здійснюється за схемою Шаміра з параметрами к=5. Необхідно:
1) обрати розмір поля GF(p), над яким здійснюється розподіл таємниці;
2) сформувати загальний секрет 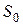 ;
;
3) обчислити часткові секрети 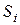 ;
;
4) сформувати загальний секрет 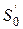 , отримавши, часткові
, отримавши, часткові 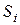 , використовуючи інтерполяційну формулу Лагранжа.
, використовуючи інтерполяційну формулу Лагранжа.
Розв’язок.
1) спочатку формуємо просте число  , наприклад, для наглядності Р=37;
, наприклад, для наглядності Р=37;
2) породжуємо випадково загальний секрет 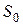 , що є елементом поля GF(p), тобто
, що є елементом поля GF(p), тобто 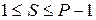 . Наприклад, S=29;
. Наприклад, S=29;
3) оскільки к=5, то формуємо випадково к-1=4 коефіцієнтів 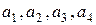 . Наприклад,
. Наприклад, 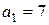 ,
, 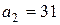 ,
, 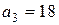 ,
, 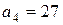 . Як
. Як 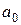 вибираємо
вибираємо 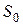 , тому
, тому  ;
;
4) присвоюємо кожному із об’єктів чи суб’єктів числові значення ідентифікаторів 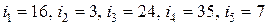 ;
;
5) поліном f(x) має вид: 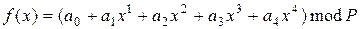 , підставимо в нього числові дані, отримаємо:
, підставимо в нього числові дані, отримаємо:
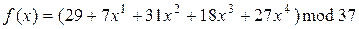 .
.
Знаходимо часткові секрети, підставивши в поліном 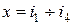 , тобто
, тобто
 ;
;
 ;
;
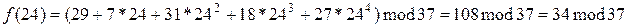 ;
;
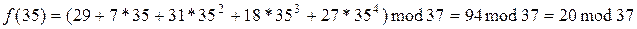 ;
;
 .
.
Таким чином: 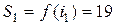 ,
,
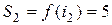 ,
,
 ,
,
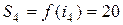 ,
,
 .
.
В подальшому 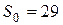 встановлюється в довірений засіб як загальний секрет. Часткові секрети
встановлюється в довірений засіб як загальний секрет. Часткові секрети 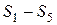 розповсюджуються в системі з забезпеченням цілісності, справжності, доступності та спостережливості.
розповсюджуються в системі з забезпеченням цілісності, справжності, доступності та спостережливості.
Нехай необхідно виробити загальний секрет, причому всі об’єкти (суб’єкти) згодні. В цьому випадку кожний з них передає свій секрет в довірений пристрій, забезпечивши їх цілісність, справжність та конфіденційність.
В засобі, якому довіряють, здійснюється відновлення f(x). Для цього використовується інтерполяційна формула Лагранжа 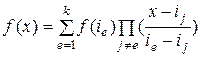 . Підставивши в цей вираз числові значення, отримаємо:
. Підставивши в цей вираз числові значення, отримаємо:

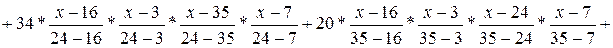
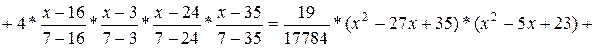
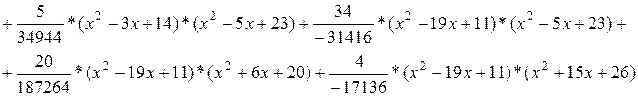
Проведемо підрахунки зворотних елементів:
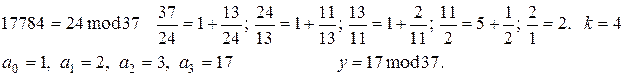
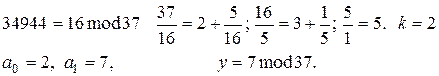



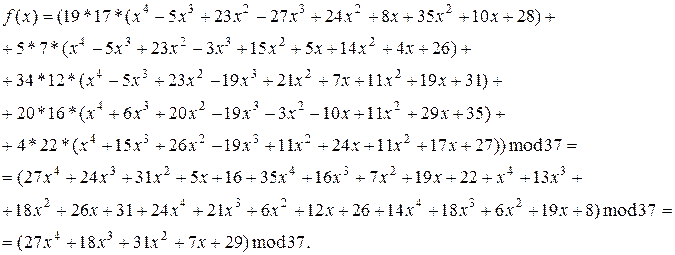
У результаті було відновлено початковий поліном, де f(0) і є загальний секрет.
Читайте також:
- Абсолютні синоніми (наприклад, власне мовні й запозичені) в одному тексті ділового стилю вживати не рекомендується.
- Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
- Альтернативність у реалізації стратегії розвитку підприємства
- АНАЛІЗ ВИРОБНИЦТВА ТА РЕАЛІЗАЦІЇ ПРОДУКЦІЇ
- Аналіз впливу факторів на зміну сумми гуртової реалізації
- Аналіз обсягу пропозиції і реалізації послуг туристського підприємства
- Аналіз стану та проблем реалізації Болонського процесу в Україні за ключовими напрямками.
- Базові та прикладні класифікації
- В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
- Валютна політика та роль НБУ в її реалізації
- Визначення і приклади
- Визначення понять: виручка від реалізації, дохід підприємства, прибуток та збиток підприємства. Методи визначення виручки від реалізації продукції
| <== попередня сторінка | | | наступна сторінка ==> |
| Протокол на основі одноразової гами | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |