
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Решето числового поля для дискретного логарифмування
29.5 (7.2.5) Порівняння складності дискретного логарифмування
29.5(7.2. 5). Квантовий алгоритм факторизації цілих чисел
Додаток А Стійкість асиметричних криптосистем, що базуються на крипто перетвореннях в простих полях. Приклади розв’язку задач та задачі для самостійного розв’язання
ОСНОВНІ ДЖЕРЕРЛА.
1. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Монографія Розд 9. Харків, ХНУРЕ, 2012 р.
2. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний конспект лекцій. (ЛК №28). Харків, ХНУРЕ, 2012 р.
3. Горбенко І. Д. Гриненко Т. О. Захист інформації в інформаційно-телекомунікаційних системах: Навч. посібник. Ч.1. Криптографічний захист інформації - Харків: ХНУРЕ, 2004 - 368 с.
4. Горбенко Ю.І., Горбенко І.Д. Інфраструктури відкритих ключів . Системи ЕЦП. Теорія та практика. Харків. Форт. 2010 , 593с.
Додаткові джерела
1.В. Задірака . Компьютерная криптологія. Підручник. К, 2002 ,504с.
2. А. Менезис, П. Ван Аршот, С. Ватсон. Руководство по прикладной криптографии CRC Press, 1997, электронная копия, 662 с
3. Брюс Шнайер. Прикладная криптография. М., изд. Триумф. 2002 г., 797 с
4. Закон України « Про електронний цифровий підпис»
Матеріал лекції
29.1 (7.2.1) Методи дискретного логарифмування в скінченному полі Галуа F(q)
На цей час відомі й доступні дві основні групи методів дискретного логарифмування в скінченному полі Галуа F(q) [4, 5, 11–13, 422, 426], що мають субекспоненційну та експоненційну складність.
До методів, що мають експоненційну складність, необхідно віднести:
- ρ-Полларда метод з евристичною оцінкою складності О(Р1/2);
- метод Поліга-Геллмана, що може бути застосований, якщо відомий канонічний розклад числа Р–1;
- метод Шенкса (малих і великих кроків).
До методів, що мають субекспоненційну складність, необхідно віднести:
- метод Адлемана (запропонований ще в 1979 р.);
- метод Купершмідта (Don Coppersmith) або COS метод (запропонований у 1986 р.);
- решето числового поля (запропоноване Д. Гордоном у 1993 р.).
Розглянемо загальну постановку розв’язання задачі дискретного логарифмування в скінченному полі Галуа та основні методи розв’язання, що мають відповідно експоненційну та субекспоненційну складність. Також зведемо оцінки складності дискретного логарифмування до таблиці, що наведена в п.9.3.4.
29.2 (7.2.2) . Дискретне логарифмування методом ρ - Полларда
Нехай 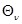 – примітивний елемент скінченного поля Галуа F(P) і Р – просте число. Тоді для кожного хi (0 < xi < P) існує однозначний хi елемент поля
– примітивний елемент скінченного поля Галуа F(P) і Р – просте число. Тоді для кожного хi (0 < xi < P) існує однозначний хi елемент поля 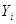 :
:
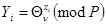 (9.32)
(9.32)
і навпаки – для кожного 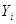 існує однозначний хi.
існує однозначний хi.
Пара 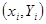 є асиметричною парою ключів криптоперетворення в скінченному полі Галуа, при чому хi – особистий (конфіденційний) ключ, а Yi – відкритий. Задача дискретного логарифмування зводиться до знаходження особистого ключа хi при відомих загальних параметрах (Р,
є асиметричною парою ключів криптоперетворення в скінченному полі Галуа, при чому хi – особистий (конфіденційний) ключ, а Yi – відкритий. Задача дискретного логарифмування зводиться до знаходження особистого ключа хi при відомих загальних параметрах (Р, 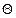 ) та відкритому ключі Yi, тобто
) та відкритому ключі Yi, тобто
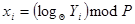 . (9.33)
. (9.33)
Розглянемо розв’язання (9.32)–(9.33) методом ρ-Полларда у загальному вигляді
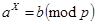 . (9.34)
. (9.34)
 |
Рис. 9.2. Крива ρ-Полларда дискретного логарифмування створення колізії
Першим методом дискретного логарифмування, очевидно, був метод ρ-Полларда (рис. 9.2). Нехай необхідно розв’язати дискретне логарифмічне рівняння (9.34) відносно Х. За своєю сутностю метод ρ-Полларда дискретного логарифмування аналогічний методу факторизації [див. п.9.2.3]. Розглянемо його детально в дещо узагальненій постановці.
Сформуємо випадкові пари цілих чисел 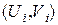 та
та  . Нехай знайдено такі дві пари чисел
. Нехай знайдено такі дві пари чисел 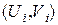 та
та  , що
, що
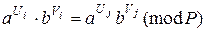 . (9.35)
. (9.35)
Підставимо (9.34) в (9.35), у результаті маємо:
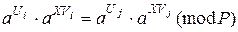
або
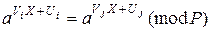 . (9.36)
. (9.36)
У порівнянні (9.36), згідно з теоремою Ойлера, степені можна прирівняти за модулем (Р-1), тобто
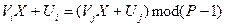 . (9.37)
. (9.37)
Із (9.37), у свою чергу, маємо:
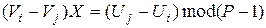
або
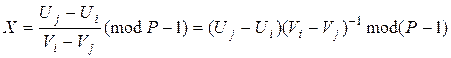 . (9.38)
. (9.38)
Таким чином, із (9.38) випливає, що необхідно знайти пари цілих чисел 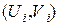 і
і 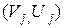 , що задовольняють (9.35), а далі, підставивши їх в (9.38), отримаємо розв’язок. По суті, алгоритм ρ-Полларда і забезпечує формування цих пар чисел.
, що задовольняють (9.35), а далі, підставивши їх в (9.38), отримаємо розв’язок. По суті, алгоритм ρ-Полларда і забезпечує формування цих пар чисел.
Наступним кроком є вибір способу формування випадкових пар чисел 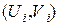 . Для цього, відповідно з рекомендаціями [5, 13, 425], виберемо в якості початкового елемент послідовності
. Для цього, відповідно з рекомендаціями [5, 13, 425], виберемо в якості початкового елемент послідовності 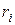
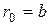 . (9.39)
. (9.39)
Далі будемо обчислювати послідовність за рекурентним правилом:
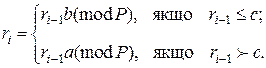 (9.40)
(9.40)
Постійну с вибирають таким чином, щоб вона перебувала між а та b приблизно на однаковій відстані. Але в більшості випадків її підбирають.
Послідовність 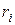 називають послідовністю ρ-Полларда. Для успішного розв’язання дискретного логарифмічного рівняння необхідно знайти два значення
називають послідовністю ρ-Полларда. Для успішного розв’язання дискретного логарифмічного рівняння необхідно знайти два значення 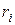 та
та 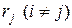 – таких, що
– таких, що
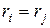 . (9.41)
. (9.41)
Після цього знаходимо значення 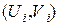 і
і 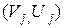 та обчислюємо згідно з (9.38) особистий ключ.
та обчислюємо згідно з (9.38) особистий ключ.
 |
Рис. 9.3. Алгоритм створення колізії
Якщо правило або залежність 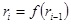 буде рандомізованим, то ймовірність колізії за аналогією з [5, 12, 13], з урахуванням рис. 9.3, визначається параметричним рівнянням:
буде рандомізованим, то ймовірність колізії за аналогією з [5, 12, 13], з урахуванням рис. 9.3, визначається параметричним рівнянням:
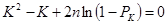 , (9.42)
, (9.42)
при
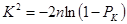 (9.43)
(9.43)
або
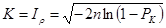 , (9.44)
, (9.44)
де К – число експериментів згідно з рис. 9.3;
n – кількість можливих значень ri;
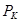 – ймовірність виникнення колізії.
– ймовірність виникнення колізії.
Для оцінки складності К потрібно задати два параметри: 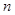 та
та 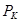 .
.
Приклад 9.3. Розв’язати дискретне логарифмічне рівняння вигляду 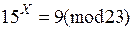 методом ρ-Полларда.
методом ρ-Полларда.
Розв’язання.:
Обчислимо 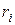 значення з урахуванням того, що
значення з урахуванням того, що 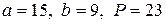 :
:
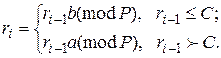
Виберемо С=6 та розрахуємо значення 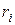 . Результати зведемо до таблиці 9.6.
. Результати зведемо до таблиці 9.6.
Таблиця 9.6
Результати розрахунків при розв’язанні дискретного логарифмічного рівняння
| І | |||||||
| ri | b=9 | ab=20 | a2b=1 | a2b2=9 | a3b2=20 | a4b2=1 | a4b3=9 |
| Ui | |||||||
| Vi |
Аналізуючи значення 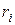 , бачимо, що r1= r4= r7, r2= r5, r3= r6. Вибравши будь-яку пару
, бачимо, що r1= r4= r7, r2= r5, r3= r6. Вибравши будь-яку пару 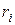 та
та 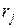 , знайдемо пари значень
, знайдемо пари значень 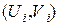 та
та 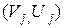 . Наприклад, для r3=r6 маємо: для r3 – Ui=2 та Vi=2; для r6 – Uj=4 та Vj=3. Підставивши ці значення
. Наприклад, для r3=r6 маємо: для r3 – Ui=2 та Vi=2; для r6 – Uj=4 та Vj=3. Підставивши ці значення
у (2.79), маємо:
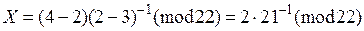 .
.
Далі знайдемо зворотний елемент y для числа 21 у кільці за модулем 22. Маємо порівняння:
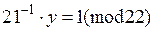 .
.
Розв’яжемо його, використовуючи алгоритм Евкліда:
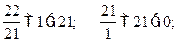
Отже, 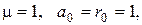 тоді
тоді
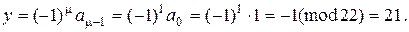
Тому
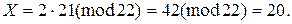
Таким чином, 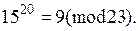 Прямим обчисленням перевіряємо правильність розв’язку.
Прямим обчисленням перевіряємо правильність розв’язку.
Приклад 9.4. Розв’язати методом ρ-Полларда порівняння 20 º7x (mod 23).
Обчислимо (9.38) таким чином:
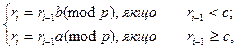
де c = 10, r0 = b = 20, a = 7.
Розв’язання.
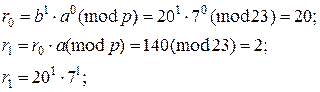
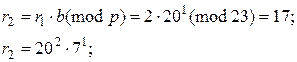
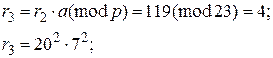
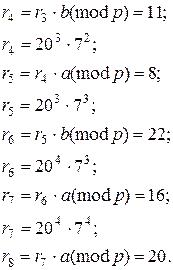
Таким чином, r8 = r0, причому r8 можна подати як
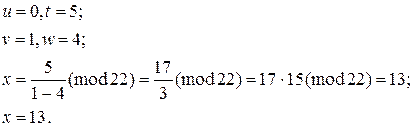
29.3 (7.2.3) Метод Поліга-Геллмана дискретного логарифмування
Метод Поліга-Геллмана дискретного логарифмування базується на китайській теоремі про лишки [13, 422, 426]. Він може бути реалізований з експоненційною складністю у разі якщо відомо розклад числа Р-1.
Нехай знову необхідно розв’язати порівняння (дискретний логарифм) вигляду
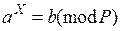 . (9.45)
. (9.45)
Розв’язання виконується в декілька етапів:
1) знаходиться канонічний розклад числа Р-1;
2) обчислюються лишки за модулями канонічного розкладу;
3) обчислюється значення Х згідно з китайською теоремою про лишки.
Перший етап виконується достатньо просто, оскільки на етапі побудови пари  розклад числа Р-1 є відомим. Інакше довести, що а – породжуючий (твірний) елемент, дуже складно. Тому на першому етапі Р-1 подається у вигляді:
розклад числа Р-1 є відомим. Інакше довести, що а – породжуючий (твірний) елемент, дуже складно. Тому на першому етапі Р-1 подається у вигляді:
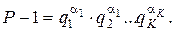 (9.46)
(9.46)
Далі знайдемо лишки 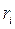 від ділення Х на
від ділення Х на 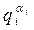 , у результаті для кожного
, у результаті для кожного 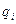 отримаємо:
отримаємо:
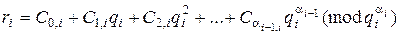 , (9.47)
, (9.47)
причому 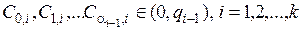 .
.
Необхідно знайти коефіцієнти 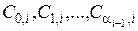 для всіх i. Оскільки лишки подано за модулем
для всіх i. Оскільки лишки подано за модулем  , то
, то
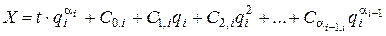 . (9.48)
. (9.48)
Запишемо далі (9.45) у вигляді
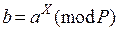 . (9.49)
. (9.49)
та піднесемо ліву і праву частини (9.49) до степеня 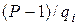 . У результаті отримаємо:
. У результаті отримаємо:
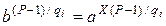 . (9.50)
. (9.50)
Обчислимо значення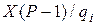 , підставивши в нього (9.48), у результаті маємо:
, підставивши в нього (9.48), у результаті маємо:
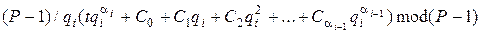 . (9.51)
. (9.51)
Якщо 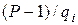 перемножити на вираз у дужках, отримаємо:
перемножити на вираз у дужках, отримаємо:
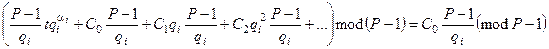 . (9.52)
. (9.52)
У цьому можна переконатися, оскільки всі члени, окрім 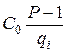 , діляться на Р-1, тому вони даватимуть лишок, який дорівнює 0. З урахуванням (9.52) вираз (9.50) має вигляд:
, діляться на Р-1, тому вони даватимуть лишок, який дорівнює 0. З урахуванням (9.52) вираз (9.50) має вигляд:
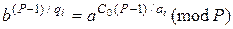 . (9.52)
. (9.52)
Тепер піднесемо ліву та праву частини (9.49) до степеня 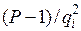 , у результаті отримаємо:
, у результаті отримаємо:
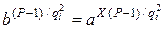 . (9.53)
. (9.53)
Підставивши у (9.53) вираз (9.48), отримаємо:
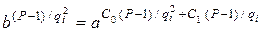 . (9.54)
. (9.54)
Оскільки на (Р-1) тепер не ділитимуться два члени
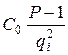 та
та 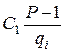 ,
,
тому вони не дорівнюють нулю.
Аналогічно можна перетворити (9.49) для всіх 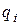 і для усіх степенів. У результаті для конкретного
і для усіх степенів. У результаті для конкретного 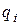 модуля степеня отримаємо
модуля степеня отримаємо 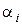 порівнянь:
порівнянь:
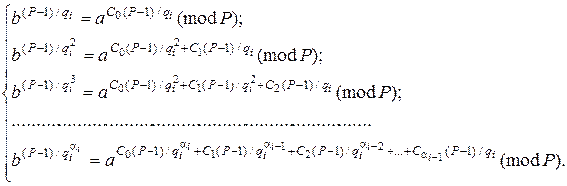 (9.55)
(9.55)
Використовуючи (9.55), можна знайти всі лишки вигляду (9.46), для цього достатньо знайти коефіцієнти 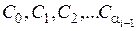 . Їх ми знаходимо, використовуючи (9.55). Спочатку, перебираючи значення
. Їх ми знаходимо, використовуючи (9.55). Спочатку, перебираючи значення 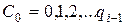 , знаходимо
, знаходимо 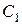 і так далі для всіх степенів, до
і так далі для всіх степенів, до 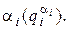 включно.
включно.
Таким чином, для фіксованого 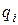 система (9.55) дозволяє визначити коефіцієнти
система (9.55) дозволяє визначити коефіцієнти 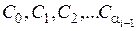 і, як наслідок, лишок (9.47). Для знаходження другого лишку необхідно взяти наступне значення
і, як наслідок, лишок (9.47). Для знаходження другого лишку необхідно взяти наступне значення 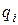 .
.
Таким чином, ми одержуємо лишки:
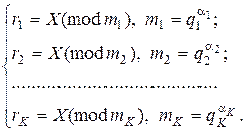 (9.56)
(9.56)
Використовуючи китайську теорему про лишки, отримаємо [422, 13]:
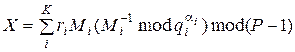 , (9.57)
, (9.57)
де 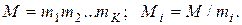
Зворотний елемент 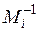 знаходимо із порівняння
знаходимо із порівняння
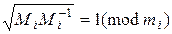 .
.
Таким чином, (9.57) дає розв’язок дискретного логарифмічного порівняння вигляду (9.45) або (9.34).
Приклад 9.5 дискретного логарифмування в скінченному полі Галуа
Розв’язати дискретне логарифмічне рівняння вигляду 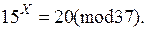 Використовуючи метод Поліга-Геллмана, що викладений вище маємо.
Використовуючи метод Поліга-Геллмана, що викладений вище маємо.
Спочатку розкладаємо число 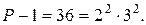
Отже 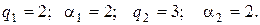
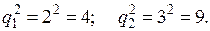
Оскільки максимальні значення степеня 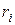 лишку
лишку 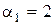 і
і 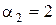 , то згідно з (9.46)
, то згідно з (9.46) 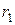 та
та 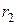 лишки матимуть тільки два члени. Тому шукатимемо
лишки матимуть тільки два члени. Тому шукатимемо 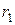 та
та 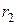 лишки за модулями
лишки за модулями 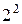 та
та 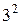 відповідно:
відповідно:
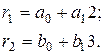
Тепер нам потрібно знайти 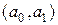 та
та 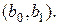 Для цього використаємо порівняння (9.55), у результаті отримаємо:
Для цього використаємо порівняння (9.55), у результаті отримаємо:
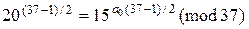 або
або 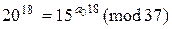 .
.
Обчисливши ліву частину, маємо:
 .
.
Далі, враховуючи, що коефіцієнти 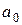 та
та 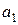 обчислюються за модулем 2, маємо, що
обчислюються за модулем 2, маємо, що 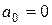 або
або 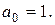 Підставивши ці значення, отримаємо, що
Підставивши ці значення, отримаємо, що 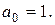 Для знаходження
Для знаходження 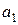 використовуємо порівняння (9.55), у результаті отримаємо:
використовуємо порівняння (9.55), у результаті отримаємо:
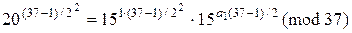 .
.
Після обчислень маємо:
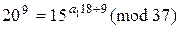 та
та 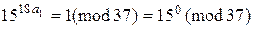 .
.
Отже, 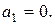 Таким чином,
Таким чином, 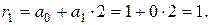
Далі за аналогією знайдемо 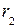 , для цього знайдемо
, для цього знайдемо 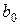 та
та 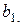 . Як і для
. Як і для 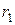 , маємо:
, маємо:
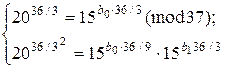
або
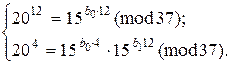
Підставимо у перше порівняння послідовно
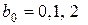 (оскільки
(оскільки 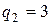 ).
).
За аналогією, як і для 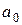 та
та 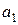 , маємо:
, маємо: 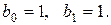 ,
,
тому 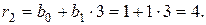
Тепер, знаючи лишки 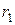 та
та 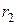 , можна знайти Х, використовуючи формулу (9.57):
, можна знайти Х, використовуючи формулу (9.57):
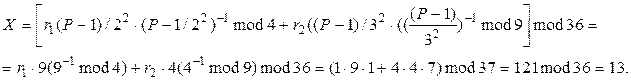
Таким чином,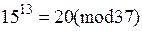 .
.
Читайте також:
- Визначення дискретного аргументу.
- Вторинні пристрої систем автоматизованого дискретного керування
- За способом одержання числового значення вимірюваної величини вимірювання поділяються на прямі, посередні, сукупні та сумісні.
- Закон розподілу та числові характеристики функції дискретного випадкового аргументу
- Первинні пристрої систем автоматизованого дискретного керування
- Приклад 3. Розв’язати лінійну задачу цілочислового програмування.
- Проблема дискретного опису еволюції системи при детерміністичному моделюванні.
- Прості і складені числа. Нескінченність множини простих чисел. Решето Ератосфена.
- Решето числового поля для дискретного логарифмування
- Решето числового поля для дискретного логарифмування
- Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу.
| <== попередня сторінка | | | наступна сторінка ==> |
| Поліноміальний метод факторизації Чалмерса | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |