• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Проблема дискретного опису еволюції системи при детерміністичному моделюванні.

Звичайно, щоб розглянути за час комп’ютерного експерименту якомога більший відрізок реального часу, намагаються зробити крок по часу якомога більшим. Однак крок по часу, тобто крок кінцево-різницевої схеми, визначає точність розрахунків характеристик системи. Зрозуміло, що для різних систем оптимальний крок по часу різний. Наприклад, для системи аргону крок становить 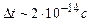, для системи міді – .

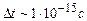Для кожної моделі в залежності від потенціалів взаємодії, чисельної схеми, граничних умов та, навіть, конкретної цілі моделювання (кожен процес має різну часову шкалу – характерний час, за який відбувається одна подія) крок по часу буде різним.

Критерію вибору кроку не існує. А досить загальне емпіричне правило вимагає, щоб флуктуації повної енергії системи не перевищували декількох відсотків від флуктуацій потенціальної енергії.

Чим практично керуватися при виборі кроку по часу? Для моделювання кристалічних систем відправною точкою можуть слугувати наступні міркування. Якщо розглядати кристал у рамках моделі Дебая (ІІ.4.4), то частоту колективних коливань можна оцінити як частоту Дебая , - міжатомна відстань. Отже, груба аналітична оцінка періоду коливань частинок у кристалі становить 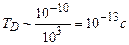. Визначити період Дебая можна також комп’ютерними методами, що може не співпадати з точним аналітичним значенням. Але ця відмінність пояснюється особливостями описаної моделі - вибором потенціалу парної взаємодії, типу кінцево-різничної схеми, граничними умовами, тощо. Тому для обраної моделі можна вважати більш придатним комп’ютерний метод оцінки періоду Дебая: атоми зафіксувати у вузлах решітки, вивести один атом з положення рівноваги і з явно меншим кроком по часу, ніж передбачуваний за аналітичною формулою, провести моделювання коливань, фіксуючи швидкість вибраного атома, - період зміни швидкості і є характерним періодом коливань атомів у системі. Зрозуміло, що для коректного моделювання крок по часу повинен становить кілька відсотків від періоду коливань .

Читайте також:

1. Cинтаксис опису змінних
2. I. Органи і системи, що забезпечують функцію виділення
3. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
4. II. Анатомічний склад лімфатичної системи
5. IV. Проблема антропогенних змін клімату або «парниковий ефект».
6. IV. Розподіл нервової системи
7. IV. Система зв’язків всередині центральної нервової системи
8. IV. Філогенез кровоносної системи
9. Iсторичне значення революції.
10. POS-системи
11. VI. Філогенез нервової системи
12. Автокореляційна характеристика системи

Переглядів: 486