
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Решето числового поля для дискретного логарифмування
У п.9.2.5 розглянуто особливості факторизації з використанням загального решета числового поля. Аналогічно і для дискретного логарифмування в скінченному полі Галуа розроблено та застосовується решето числового поля (NFS). Як буде показано нижче, воно є найбільш ефективним щодо мінімальної складності дискретного логарифмування в скінченному полі Галуа. Розглянемо сутність основних етапів застосування решета числового поля при вирішенні задач дискретного логарифмування, яке зводиться до виконання таких етапів [426, 427]. При цьому як основоположну візьмемо роботу [427].
1. Спочатку обирається два багаточлени невеликого степеня f1(x) та f2(x), що є незвідними в Z[x] з малими коефіцієнтами, але такі, що f1(x) та f2(x), мають спільний корінь m у полі F(Р). Ці багаточлени визначають два числових поля Q (a1) та Q (a2). Оскільки m – корінь, то існує гомоморфізм φj кільця Z [aj] для поля F(Р) (j ={1, 2}), але такий, що φj(aj) = m. Далі розширимо φj до поля Q (aj), не звертаючи уваги на потенційні проблеми існування подільності.
2. Кільце цілих чисел, не обов’язково буде унікальною фактор-базою, але кільце отриманих після ділення ідеалів буде завжди.
3. Для побудування решета NFS формуються дві фактор бази з ідеалів B1 та B2 (відповідно Q (a1) та Q (a2)), що складаються з простих гладких ідеалів. При цьому поняття гладкості визначається таким чином: отриманий після ділення ідеал I з Q (aj) є гладким, якщо він може бути розкладений за фактор-базою Bj, та алгебраїчне число x є гладким, якщо отриманий після ділення ідеал áxñ вибрано з гладкого діапазону.
4. Етап просіювання здійснюється в такій послідовності. Спочатку знаходимо велику кількість пар малих цілих чисел (ai, bi), але таких, що 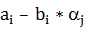 – гладкі, тобто результат факторизації
– гладкі, тобто результат факторизації 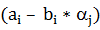 відомий.
відомий.
5. Розглядаються числа поля Q (a1) для лінійної алгебри за модулем р -1, а потім виробляється багато цілочисленних векторів (еi) – таких, що отриманий після ділення ідеал
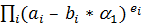
є (р-1)-го степеня. Але це не обов’язково виконується, тобто не означає, що алгебраїчне число
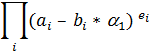
є (р -1)- го степеня в Q (a1). Однак, з використанням конкретних лінійних відображень з
Q (a1) у Z(p-1) Schirokauer (Широкаєру) [428] вдалося додати декілька лінійних рівнянь для того, щоб
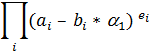
було (р -1)-им степенем в Q (a1).
Виходячи з цього, маємо, що
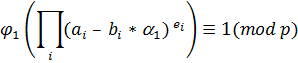
Отже, 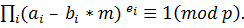
Далі, логарифмуючи (9.58), отримаємо, що
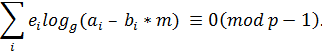
З іншого боку, кожне 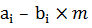 має бути гладким, бо
має бути гладким, бо 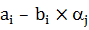 є гладким.
є гладким.
Тому попереднє рівняння може бути подане у вигляді:
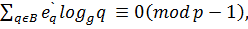
де В – набір невеликих простих чисел, і кожне  – відоме ціле число.
– відоме ціле число.
Для розв’язання задачі дискретного логарифмування потрібно отримати велику кількість таких лінійних рівнянь, а ще більше – для поля Q (a2).
6. Коли рівнянь буде достатньо, можна буде розв’язати задачу дискретного логарифмування таким чином.
Для обчислення дискретного логарифма b = ах mod р достатньо знайти
експоненту еi Z – таку, що
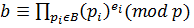 ,
,
де кожне pi – «добре» просте число, а не тільки pi 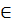 B, оскільки тільки для «добрих» простих чисел відомі логарифми.
B, оскільки тільки для «добрих» простих чисел відомі логарифми.
7. Є кілька способів, щоб знайти такі показники. Наприклад, при використанні двовимірної решітки скорочення можна обчислити два лінійно незалежних цілочисленних вектори (A1, B1) і (A2, B2) з координатами 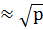 , такі як
, такі як
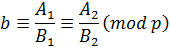
Звідси випливає, що для будь-яких цілих чисел a а також b:
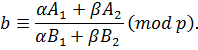
Тепер, оскільки Ai та Bi достатньо малі, то можна, використовуючи техніку просіювання, спробувати знайти пару (a,b), але таку, що 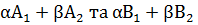 є гладкими при «добрих» простих числах. Якщо жоден кандидат не знайдено протягом розумного періоду часу, то спроби потрібно повторити, наприклад, замінити b на bsi, де s є найбільшим «добрим» числом.
є гладкими при «добрих» простих числах. Якщо жоден кандидат не знайдено протягом розумного періоду часу, то спроби потрібно повторити, наприклад, замінити b на bsi, де s є найбільшим «добрим» числом.
Оцінка складності дискретного логарифмування за умови застосування решета числового поля наводиться нижче, у підрозділі 9.3.4.
29.5 (7.2.5) Порівняння складності дискретного логарифмування
У роботах [4, 5, 11–13, 422–424, 426–428] запропоновано значне число моделей оцінки складності дискретного логарифмування. Основним етапом криптоаналізу є дискретне логарифмування. У табл. 9.7 наведені аналітичні вирази, що можуть бути застосовані для оцінки складності відповідних методів дискретного логарифмування. Їх аналіз підтверджує висновок про те, що методи ρ-Полларда, Поліга-Геллмана мають експоненційну складність дискретного логарифмування. Методи Адлемана, Купершмідта й решета числового поля мають субекспоненційну складність дискретного логарифмування. Причому в [426] та [427] наведено аналітичні вирази, що відрізняються. Скоріше за все вони враховують особливості дискретного логарифмування і є певними оцінками. Детальний розгляд цього факту виходить за межі можливостей цієї монографії. Для більш детального освоєння методу дискретного логарифмування в скінченному полі Галуа можна скористатися роботою [426] і роботами, на які є посилання в ній. Загальним же висновком є те, що найбільш простим (швидким) методом дискретного логарифмування є решето числового поля.
Таблиця 9.7
Складність дискретного логарифмування
| Назва методу | Складність методу |
| ρ-Полларда метод | О(P1/2) |
Метод Поліга-Геллмана при P-1 = 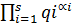
| О(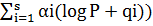 ) )
|
Метод Адлемана (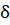 , v – константи), 0≤v<1 , v – константи), 0≤v<1
| О(exp (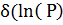 Ln(ln (P)))v)) Ln(ln (P)))v))
|
Метод Купершмідта (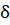 =1,56, v=1/2) =1,56, v=1/2)
| О(exp (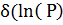 Ln(ln (P)))v)) Ln(ln (P)))v))
|
| Метод решета числового поля [426] | О(exp (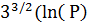 ln ln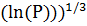 ) )
|
| Метод решета числового поля [427] | exp ((64/9)1/3 (ln q)1/3(ln ln q)2/3). |
Серед суб експоненційних за складністю методів необхідно відмітити таке.
Метод Адлемана з’явився ще в 1979 році. Це був перший метод, що мав субекспоненційну складність дискретного логарифмування. Для нього v =1/2, а с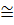 2.
2.
Метод Купершмідта (Don Coppersmith), або COS метод, був запропонований декількома математиками [426]. Для цього методу v =1/2, а с=1. З його застосуванням у 1997 році було практично розв’язано задачу дискретного логарифмування з розміром модуля Р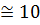 85. Також вважається, що метод Купершмідта є більш швидким за решето числового поля при Р
85. Також вважається, що метод Купершмідта є більш швидким за решето числового поля при Р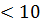 90.
90.
Решето числового поля вперше було запропоноване Д. Гордоном у 1993 році. Для нього було обгрунтувано оцінку вигляду
О(exp (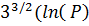 ln
ln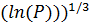 ), (9.58)
), (9.58)
але воно було не практичним, тому в подальшому було декілька разів удосконалено. Також було показано, що при Р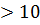 100 решето числового поля є більш швидким (менш складним), ніж решето Гордона.
100 решето числового поля є більш швидким (менш складним), ніж решето Гордона.
Згідно даних [426], на сьогодні максимальним дискретним логарифмом, що розв’язаний практично, є дискретний логарифм розміром Р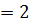 907 (273 десяткових цифр). Відповідні доступні відомості щодо сучасних досягнень дискретного логарифмування в скінченному полі Галуа наведені в табл. 9.7.
907 (273 десяткових цифр). Відповідні доступні відомості щодо сучасних досягнень дискретного логарифмування в скінченному полі Галуа наведені в табл. 9.7.
Таблиця 9.8
Досягнення криптоаналізу (дискретного логарифмування) DSA
| Рік | Довжина ключа, бітів | Час, MIPS-років | Пам’ять ОЗУ/HDD, Гб |
| DSA | |||
| 0,256 /5 | |||
| 2,775*108 | 1/35 |
29.6(7.2.6). Алгоритм факторизації цілих чисел
Для рішення задачі факторизації використається алгоритм знаходження на квантовій обчислювальній системі періоду (порядку) r числа x у мультиплікативній групі лишків по модулі факторизуємого числа N [3,5]. Така група є циклічною.
Нехай необхідно факторизовати число N. При цьому досить знайти хоча б один множник факторизації. На першому етапі вибирається довільне число X, що є взаємно простимо із числом N. Потім розглянемо послідовність, утворену функцією:
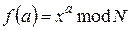 . (1)
. (1)
Послідовності {ха}і {xa mod N} виглядають у такий спосіб:
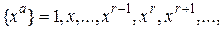 (2)
(2)
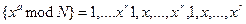 (3)
(3)
Число r – мінімальний ступінь, для якої
xr =l(mod N). (4)
Вираження треба з узагальнення теореми Эйлера, відповідно до якої для будь-яких взаємно простих чисел a і n
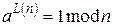 (5)
(5)
де L(n)– узагальнена функція Эйлера.
У залишковому підсумку завдання факторизации числа N полягає в складності пошуку періоду r числа х (4). При більших N потрібен перебір досить великої кількості варіантів а. Ефективний алгоритм пошуку періоду r, в основі якого лежить модель квантового паралелізму, наведень нижче.
Нехай період r знайдений. Якщо період непарний, вибирається нове число X і алгоритм пошуку r повторюється. Якщо алгоритм парний, приступаємо до виконання факторизації. Вираження (4) може бути записане в наступному виді:
xr – 1= 0(mod N). (6)
Звідси треба:
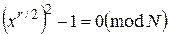 . (7)
. (7)
Далі:
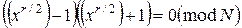 . (8)
. (8)
З виразу (8) треба, що добуток двох співмножників кратний числу N. Таким чином, один зі співмножників винний мати з N загальний множник. Остаточний етап факторизації полягає в пошуку найбільшого загального дільника співмножників:
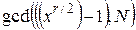 . (9)
. (9)
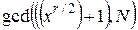 . (10)
. (10)
Знайдене значення gcd є шуканим числом.
Нижче подано приклад факторизації. Нехай необхідно факторизувати число N = 91. Виберемо х = 3. Обчислимо послідовності
а: 0, 1, 2, 3, 4, 5, 6, 7,...
3a: 1, 3, 9, 27, 81, 243, 729, 2187, ...
3amod91: l, 3, 9, 27, 81, 61, 1, 3,...
Таким чином, шукане значення r = 6. Далі одержуємо:
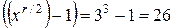 . (11)
. (11)
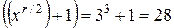 . (11)
. (11)
Знаходимо за допомогою алгоритму Евкліда (алгоритм Евкліда має поліноміальну складність):
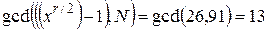 . (9)
. (9)
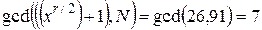 . (10)
. (10)
Отримані значення 7 і 13 є результатом факторизації числа N = 91.
III Алгоритм пошуку періоду r Шора
Для пошуку періоду r реалізується квантова система, що складається із двох регістрів [3-7]:
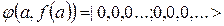 (15)
(15)
Довжина регістрів вибирається таким чином, щоб перший регістр міг умістити максимально-допустимое значення а (довжини т) вираження (1), а другий регістр міг умістити число N (довжини l).
1. Для кубіта регістра 1 виконується перетворення Адамара-Уолша, що може бути представлене наступною матрицею:
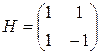 , (16)
, (16)
т. б. квантові стан перетворяться в такий спосіб: 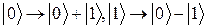 . При цьому перший регістр переводитися в суперпозицію станів всіх припустимих аргументів:
. При цьому перший регістр переводитися в суперпозицію станів всіх припустимих аргументів:
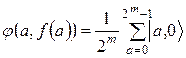 (17)
(17)
2. Використовуючи квантовий паралелізм обчислюється значення функції (1) для можливого а. Результат (суперпозиція результатів) міститься в другий регістр. При цьому квантова система переводитися в стан:
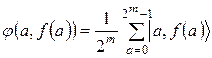 (18)
(18)
При цьому функція f(a) має вигляд, подань на мал. 1.
3. Робиться вимір fc одного отриманого результату функції f(a). При цьому хвильова функція проектується в суперпозицію станів:
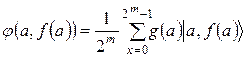 . (19)
. (19)
де
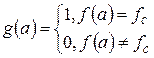 (20)
(20)
Т. б., квантова система містить тільки стану аргументу а, для яких значення функції f(c)дорівнює обмірюваному fc; хвильова функція в цьому випадку є періодичною з періодом r.
4. Для добування періоду необхідно виконати перетворення Фур'є хвильової функції (19). При цьому використається реалізація квантового перетворення Фур'є, що має наступний вид:
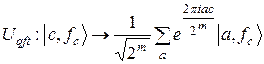 . (21)
. (21)
У випадку перетворення Фур'є дискретної періодичної функції одержуємо спектр, що містить спектральні «сплески», пов'язані з періодом вихідної періодичної функції. Для квантової системи одержуємо наступну хвильову функцію:
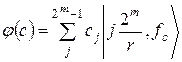 . (22)
. (22)
Квантова система переводитися в суперпозицію станів. При цьому перший регістр містять значення, обернено пропорційні r. Спектр має вигляд, подань на малий. 2.
5. Виробляється вимір першого регістра. Виходить значення:
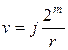 , (23)
, (23)
де r – шуканий період, j – невідомий індекс спектрального сплеску. Вираження (19) може бути представлене в наступному виді:
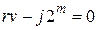 . (24)
. (24)
У даному вираженні v – обмірюване значення першого регістра, r – шуканий період, j – невідомий індекс обмірюваного регістра. У даному рівнянні необхідно знайти r і j. Дане рівняння є діафантовим. Існує ефективний (поліноміальний) алгоритм рішення рівняння виду (24) з використанням ланцюгових дробів. Якщо знайдене значення r є парним, воно використається для факторизации числа N (8) - (10). У противному випадку алгоритм повторюється з іншим обраним значенням X (вираження (1)).
Даний алгоритм має поліноміальну складність, тому що засновано на ефекті квантового паралелізму й не вимагає перебору варіантів аргументів функції (1).
IV Моделювання алгоритму квантових обчислень Шора
Наведень вище алгоритм був промодельований з використанням традиційних алгоритмічних і обчислювальних механізмів.
На мал. 1 подань розподіл значення функції f(a)= xa mod N (dependence of result on argument), а її спектра 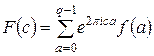 (dependence of amplitude module on argument) – на малий. 2.
(dependence of amplitude module on argument) – на малий. 2.
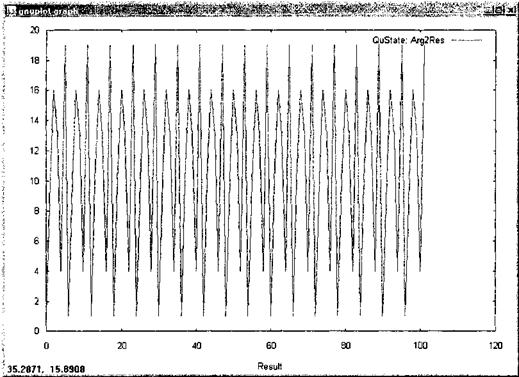
 Малюнок 1
Малюнок 1
У зв'язку з тім, що обчислення проводяться в Гильбертовом просторі, система моделювання є досить вимогливою до ресурсів (до пам'яті й продуктивності процесора).
При факторизации чисел необхідно враховувати, що потрібна пам'ять для зберігання відображення системи розраховується в такий спосіб:
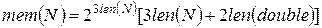 , (25)
, (25)
де len – функція, що повертає довжину аргументу в бітах.
Наприклад, при факторизации числа N = 21,1еп(21) = 5система моделювання використає не менш 2528·1024 біт. Для факторизации числа len(N)= 16 буде потрібно не менш 30064771072 Mb.
Проведено аналіз алгоритму факторизації Шора, що дозволяє вирішувати задачі факторизації цілих чисел з поліноміальною складністю.
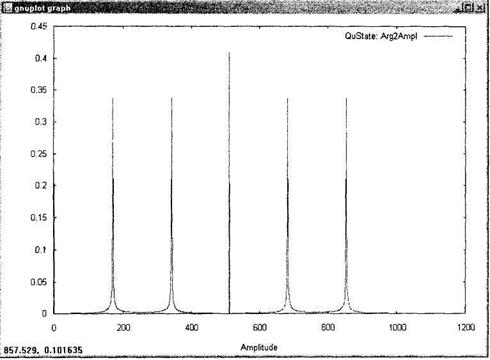
Малюнок 2
V Висновок
Слід зазначити, що нині існує всього лише кілька алгоритмів в основному для NP-повних завдань: алгоритм факторизації цілих чисел, алгоритм рішення задачі дискретного логарифмування, і алгоритм пошуку елемента в несортованій базі. Як і раніше на даному етапі є відкритою проблема можливості створення універсального рішення, що дозволяє вирішувати широке коло NP-повних завдань із поліноміальною складністю. Рішення даної проблеми може розширити коло можливостей обчислювальної техніки в областях, зв'язаних як з моделюванням квантово-механічних фізичних процесів, ефективним рішенням завдань штучного інтелекту, так і ефективним рішенням завдань криптоаналізу несиметричної криптографії.
Додаток А Стійкість асиметричних криптосистем, що базуються
на криптоперетвореннях в простих полях. Приклади розв’язку задач
та задачі для самостійного розв’язання
Читайте також:
- Визначення дискретного аргументу.
- Вторинні пристрої систем автоматизованого дискретного керування
- За способом одержання числового значення вимірюваної величини вимірювання поділяються на прямі, посередні, сукупні та сумісні.
- Закон розподілу та числові характеристики функції дискретного випадкового аргументу
- Первинні пристрої систем автоматизованого дискретного керування
- Приклад 3. Розв’язати лінійну задачу цілочислового програмування.
- Проблема дискретного опису еволюції системи при детерміністичному моделюванні.
- Прості і складені числа. Нескінченність множини простих чисел. Решето Ератосфена.
- Решето числового поля для дискретного логарифмування
- Решето числового поля для дискретного логарифмування
- Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Приклад 2. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |