
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Логічні моделі
Функціональні моделі
Функціональна модель являє собою сукупність функціональних елементів, кожний із який має велику кількість входів і один вихід. Функціональні моделі дуже широко використовуються в завданнях контролю і діагностики. Вони мають порівняно високу універсальність і в той же час достатню абстрактність. Крім того, вони дозволяють легко одержувати інші види моделей, наприклад, граф-моделі і їхні аналоги.
Одна з найважливіших різновидів функціональної моделі є так звана таблиця станіваботаблиця несправностей.
Логічні моделі будуються на основі двозначної логіки (справний-несправний). Логічні моделі є складними булевими функціями, що залежать від ряду змінних, кожна з яких може приймати значення 0 або 1 у залежності від стану відповідного функціонального елемента об'єкта.
Логічні моделі можуть застосовуватися для опису різних об'єктів діагностики, але найбільш зручні вони для опису дискретних об'єктів, наприклад релейно-контактних схем.
Слід зазначити, що функціональні і логічні моделі, а такожїхні різні модифікації найбільшою мірою в порівнянні з іншими задовольняють перерахованим вище вимогам до моделей об'єктів контролю і діагностики. Тому розглянемо більш докладно ці два види моделей і оцінимоїхні можливості при діагностиці різних об'єктів.
ФУНКЦІОНАЛЬНІ МОДЕЛІ
Функціональна модель являє собою графічне зображення схеми об'єкта із зазначенням усіх функціональних зв'язків між окремими його елементами. Головна перевага функціональної моделі - її фізична наочність, тому що у ній в більшій мірі в порівнянні з іншими моделями відображається структура реального об'єкта.
При побудові цієї моделі передбачається, що систему, розглянуту як об'єкт діагностики, можна підрозділити на деяку кількість зв'язаних між собою функціональних елементів. Під функціональним елементом розуміється частина системи, що може знаходитися в одномуз двох несумісних станів (працездатна, відмовила) і в працездатному стані відповідає необхідною реакцією на визначену сукупність впливів, до яких можуть входити реакції інших елементів.
Впливи, що необхідно прикласти до працездатного елемента для одержання необхідної реакції, називають припустимими. Реакція елемента, що відмовив, називається неприпустимою. Неприпустимою називають також реакцію працездатного елемента при неприпустимому вхідному впливі. Кожний функціональний елемент моделі може мати декілька входів і один вихід. Цим функціональна модель об’єкту відрізняється від його звичайної функціональної схеми, у якій елементи можуть мати декілька виходів, тобто елемент функціональної моделі відрізняється від реального елемента звичайної схеми, складеної з урахуванням зручності опису процесів функціонування об'єкта. При складенні функціональної моделі реальний елемент, що має n виходів, поділяється на п первинних функціональних елементів.
Для того щоб цілком задати функціональну модель, необхідно:
а) перерахувати всі можливі для даної системи комбінації елементів, що одночасно відмовили, тобто задати безліч можливих станів системи;
б) зазначити, які комбінації припустимих впливів необхідно прикласти до кожного елемента для одержання припустимої реакції;
в) задати схему об'єкта, на якій зазначені всі елементи і зв'язки міжними.
Приклад графічного зображення функціональної моделі показаний на рисунку.
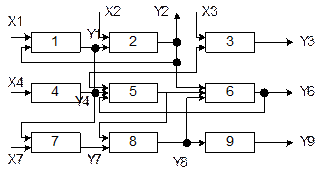
Рисунок - Функціональна модель системи
Функціональна модель дозволяє однозначно визначити перевірки, що необхідно робити з метою пошуку всіх елементів, що відмовили. Кожна перевірка полягає в формуванні припустимих впливів на елементи і контроліїх реакції. Для визначення мінімальної сукупності параметрів, що залежала б від стану усіх функціональних елементів, складають таблицю взаємозалежності вихідних параметрів, кількість рядків і стовпців якої збігається з кількістю елементів.
| yi | Елементи об’єкта модели | ||||||||
| Y1 | + | + | |||||||
| Y2 | + | + | |||||||
| Y3 | + | + | |||||||
| Y4 | + | ||||||||
| Y5 | + | + | + | + | + | + | + | ||
| Y6 | + | + | + | + | + | + | + | ||
| Y7 | + | + | |||||||
| Y8 | + | + | + | + | + | + | + | ||
| Y9 | + | + | + | + | + | + | + | + |
Аналізуючи функціональні зв'язки елементів і позначивши знаком "+" наявність залежності виходу yi від стана відповідного j-го елемента, одержуємо для розглянутого прикладу функціональної моделі таблицю, з якої видно, що кожний з трьох наборів вихідних параметрів {y3,y5,y9},{y3,y6,y9} і {y3,y8,y9} забезпечує повний контроль працездатності системи.
Остаточне рішення, тобто вибір однієї з цих сукупностей параметрів можна прийняти на основі оцінки тих витрат, із якими зв'язана реалізація контролю по кожній з цих сукупностей параметрів. За допомогою функціональної моделі може бути побудована граф-модель об'єкта контролю, заснована на застосуванні термінології і методів теорії графів. Побудова моделі у виді орієнтованого графа ґрунтується на наступних положеннях:
а) кожний функціональний елемент зображується у вигляді вершини графа;
б) функціональні зв'язки замінюються дугами зв'язку графа, напрямок яких збігається з напрямком проходження сигналів;
в) нумерація вершин графа повинна збігатися з нумерацією елементів;
г) пристрій, на який поступають вихідні сигнали, або зовнішнє середовище, із яким воно зв'язане, зображується у вигляді окремої вершини графа.
Для розглянутого приклада побудована граф-модель має вигляд, зображений на рисунку.
Маючи безліч перевірок можна побудувати таблицю несправностей, що буде містити всі необхідні дані для побудови діагностичних тестів. Для побудови таблиці несправностей необхідно для кожного стана об'єкта визначити вихід перевірки контрольованих виходів. При цьому позитивний вихід перевірки позначається одиницею, якщо реакція і-го елемента припустима, а негативний - нулем, якщо реакція і-го елемента неприпустима.

| S | Стан елементів | Перевірки | ||||||||||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y8 | Y9 | |
Ця таблиця складена в припущенні, що одночасно можлива відмова тільки одного елемента.
З приведеної таблиці видно, що відмови елементів 1 і 2 виявляють себе однаково. То ж саме можна сказати і про елементи 5, 6 і 8. Такі відмови називають нерозрізненими. Нерозрізненим відмовам відповідають тотожні рядки таблиці несправностей. Для усунення нерозрізненості відмов необхідно або провести додаткові перевірки, або змінити структуру об'єкта розривом зворотних зв'язків.
Розглянута вище функціональна модель є зручної, формою представлення електроавтоматичних і радіоелектронних пристроїв, що здійснюють перетворення безупинних сигналів. Однак для цілого ряду технічних систем припущення, на яких заснована ця функціональна модель, не виконуються. Зокрема, у деяких системах неприпустима реакція одного або декількох елементів не тягне за собою неприпустиму реакцію інших елементів. Таке явище має місце, наприклад, у системах із резервуванням елементів, у комбінаційних схемах і кінцевих автоматах.
Таблиця несправностей містить вихідні дані, необхідні при побудові діагностичного тесту або програми діагностики об'єкта. При побудові таблиць несправностей можна не враховувати специфіку окремих систем і думати, що будь-яка таблиця, що задає зв'язок між безліччю станів системи, безліччю можливих перевірок безліччю виходів цих перевірок, є таблицею несправностей. При такому підході таблицю несправностей можна розглядати як деяку досить абстрактну модель об'єктів діагностики, що охоплює практично всі реальні технічні системи.
Логічна модель
Основою для побудови логічної моделі є функціональна схема об'єкта. Припустимо, що об'єкт складаєтьсяіззв'язаних між собою функціональних елементів, кожний з яких має вхідні і вихідні сигнали, що позначаються далі через хk і уk відповідно. Будь-який вхідний сигнал може належати області припустимих значеньабо виходити з неї, тобто вхідний вплив може бути припустимим або неприпустимим. Тому розміри хк можна розглядати як логічні перемінні, що приймають тільки два значення: 1 і 0.
Вихідні сигнали уk також можуть бути припустимими або неприпустимими, тобто вони приймають тільки два значення: 1 і 0. Але на відміну від вхідних впливів уk не є логічними змінними, тому що вихідні сигнали будь-якого технічного пристрою залежать від вхідних впливів. У даному випадку для кожного вихідного сигналу к-го функціонального елементу можна записати:
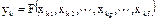
причому функція уk може приймати два значення: 1 і 0.
Функція 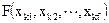 що приймає значення 0 і 1 і залежить від змінних, кожна з яких може приймати також значення 0 і 1, називається булевою або перемикальною функцією. Областю визначення булевої функції служить сукупність усіляких f - мірних наборів з 0 і 1, а для її завдання досить зазначити, які значення функції відповідають кожному з цих наборів. Таким чином, для всіх можливих сполучень входів к-го функціонального елемента (думаємо, що розглянутий функціональний елемент знаходиться в справному стані) ми можемо на основі аналізу функціональних зв'язків елемента визначити відповідні значення вихідного сигналу уk, який нас цікавить. Ці дані можна звести в таблицю. Якщо ми розглядаємо f вхідних сигналів, кожний із який може приймати значення 0 і 1, то загальна кількість f - мірних наборів із 0 і 1, тобто кількість рядків таблиці, дорівнює 2f . Правий стовпець таблиці буде містити значення уk, що відповідають кожному з наборів. Ця таблиця визначить булеву функцію
що приймає значення 0 і 1 і залежить від змінних, кожна з яких може приймати також значення 0 і 1, називається булевою або перемикальною функцією. Областю визначення булевої функції служить сукупність усіляких f - мірних наборів з 0 і 1, а для її завдання досить зазначити, які значення функції відповідають кожному з цих наборів. Таким чином, для всіх можливих сполучень входів к-го функціонального елемента (думаємо, що розглянутий функціональний елемент знаходиться в справному стані) ми можемо на основі аналізу функціональних зв'язків елемента визначити відповідні значення вихідного сигналу уk, який нас цікавить. Ці дані можна звести в таблицю. Якщо ми розглядаємо f вхідних сигналів, кожний із який може приймати значення 0 і 1, то загальна кількість f - мірних наборів із 0 і 1, тобто кількість рядків таблиці, дорівнює 2f . Правий стовпець таблиці буде містити значення уk, що відповідають кожному з наборів. Ця таблиця визначить булеву функцію 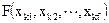 що встановлює зв'язок виходу уk із безліччю входів хк[p=1(1)f] іноді називається функцією умов роботи к-го функціонального елемента за виходом уk.
що встановлює зв'язок виходу уk із безліччю входів хк[p=1(1)f] іноді називається функцією умов роботи к-го функціонального елемента за виходом уk.
Для приклада розглянемо функціональний елемент об'єкта, зображений на рисунку.
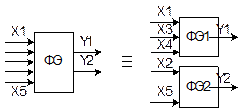
Функціональний елемент ФЭ має п'ять входів (х1-х5) і два виходи (у1,у2). Очевидно що загальна кількість можливих сполучень значень вхідних сигналів дорівнює 25=32. Значення у1 і у2 для кожного такого сполучення можна визначити експериментальним шляхом подачі на вхід свідомо справного елемента ФЭ відповідній комбінації значень х1-х5.Дані експерименту заносимо в таблицю.
| n | x1 | x2 | x3 | x4 | x5 | y1 | y2 |
| ... | |||||||
| … | |||||||
Основною перевагою логічної моделі є можливість використання без відкидання резервних елементів системи.
Читайте також:
- II. Діалогічні
- VІ. Структурно-логічні схеми
- Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
- Агроекологічні проблеми розвитку і шляхи їх розв'язання
- Аналіз економічноїї політики за допомогою моделі Мандела-Флемінга. Випадки вільного та фіксованого валютного курсів.
- Аналітичний підбір математичної моделі.
- Анатомо-фізіологічна перебудова організму підлітка та її вплив на його психологічні особливості й поведінку.
- Анатомо-фізіологічні основи статевого розвитку.
- Анатомо-фізіологічні особливості молодших школярів
- Антигени. Антитіла. Серологічні реакції .
- Антропогенний вплив на природне середовище та сучасні екологічні проблеми
- Антропогенні екологічні катастрофи
| <== попередня сторінка | | | наступна сторінка ==> |
| Графічні і графоаналітичні моделі | | | Тема 6: Асоціалізація, десоціалізація та ресоціалізація особистості |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |