• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Графічні і графоаналітичні моделі

Непараметричні моделі

Поліноміальні моделі

Для великої кількості об'єктів найчастіше неможливо знайти точні аналітичні вираження дляїхніх операторів. У цих випадках зв'язок між вхідними і вихідними сигналами об'єкта апроксимується різними поліномами, рядами, ортогональними розкладеннями або рівняннями регресії. Точність апроксимації досягається за рахунок вибору виду полінома, його порядку і вдалого підбору коефіцієнтів. По своїй сутності поліноміальні моделі відносяться до параметричних моделей, тому що наявні в них коефіцієнти зв'язані зі значеннями параметрів об'єкта. Однак цей зв'язок не явний, що утрудняє можливість використання цих моделей для оцінки працездатності об'єкта, не говорячи вже про локалізацію в ньому несправностей. Разом з тим вони вигідно відрізняються від параметричних моделей більш високим рівнем формалізму і більшої універсальності в змісті використанняїх для різних систем (лінійних і нелінійних, дискретних і т.д.).

Відносяться перехідні функції, імпульсні перехідні функції і спектральні характеристики. Використання цих моделей із метою контролю працездатності об'єкта в ряді випадків більш прийнятні у порівнянні з параметричними моделями, тому що вони дають більш точні результати контролю. Особливо ці моделі широко використовуються для контролю і діагностики механічних об'єктів (наприклад, при акустичній діагностиці). Але для пошуку несправностей у електроавтоматичних і радіоелектронних системах вони малопридатні.

До подібних моделей відносяться схеми, графи, діаграми, таблиці і т.д. Однією з таких моделей є так називана діаграма проходження сигналів. Графічно вона представляється у вигляді схеми, що складається з вузлів, з'єднаних спрямованими гілками, які зображують систему алгебраїчних рівнянь. Вузли діаграми відповідають перемінним, а гілки - операторам, що характеризують коефіцієнти при перемінних. Діаграма проходження сигналів найчастіше може бути побудована тільки на підставі аналізу структури об'єкта без укладання рівнянь.

Кожній гілці, що з'єднує два вузли, відповідає свій оператор, позначений Т_ij, де i - означає вузол, відкіля починається гілка, j - вузол, де гілка закінчується. Напрямок гілки вказується стрілкою.

Кожному вузлу відповідає своя змінна (сигнал). Сигнал кожного вузла 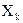дорівнює сумі вхідних сигналів: 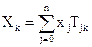(k=1,2,3,....).

При цьому кожний вхідний сигнал дорівнює добутку оператора вхідної гілки на сигнал вузла, із якого гілка виходить. По своїй сутності розглянута діаграма являє собою орієнтований граф і може бити описана в термінах теорії графів.

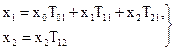
Для приклада розглянемо діаграму проходження сигналів.

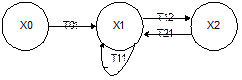
Із неї видно, що існують гілки різних типів. Гілка, у якої оператор має індекси, розташовані в порядку зростання (Т₀₁, Т₁₂), називається прямою; гілка, у якої оператор має індекси, розташовані в порядку убування (Т₂₁), - зворотною. Декілька послідовно з'єднаних гілок являють собою шлях від одного вузла до іншого. Замкнутий шлях являє собою контур зворотного зв'язку, що може бути утворений однієї (Т₂₁) або декількома гілками (Т₁₂, Т₂₁).

Діаграма проходження сигналів дозволяє вирішувати ряд важливих завдань діагностики. Спостерігаючи за деформацією контрольованих сигналів і порівнюючи їх із раніше складеною діаграмою, ми можемо судити про працездатність об'єкта і виявити причину зміни вихідних сигналів.

У ряді випадків діаграми проходження сигналів дозволяють розкрити не цілком очевидні, але важливі для рішення завдань діагностики властивості об'єкта. Крім того, відволікаючись від фізичної сутності зв'язків і перемінних, наявних в об'єкті, і користуючись досить простими правилами, ми можемо перетворити діаграму проходження сигналів і знайти всі можливі рішення рівнянь, що описують об'єкт.

Недоліком розглянутої моделі є те, що вона може бути застосовна для діагностики нескладних об'єктів, функціонування яких описується алгебраїчними рівняннями (електричних схем і контурів).

Для діагностики більш складних об'єктів використовують так звану граф-модель, що являє собою орієнтований граф. Вершинами графа є функціональні елемент об'єкта, а дугами - зв'язки міжними. У такому вигляді граф-модель досить широко використовується в завданнях діагностики, причому не стільки для безпосереднього відшукання несправностей, скільки для побудови інших різновидів моделей (наприклад, матриць шляхів, суміжності і інциденцій, таблиці несправностей і ін.) і для укладання на їхній основі формалізованих правил і алгоритмів обробки діагностичної інформації. Питання практичного використання граф-моделей іїхніх табличних аналогів у завданнях діагностики більш докладно розглядаються в наступних параграфах.

Для складних об'єктів укладання граф-моделі являє собою досить трудомістку роботу, причому через велику кількість функціональних елементів і зв'язків між ними граф-модель утворюється дуже складна. Це є недоліком даного класу моделей. Крім того, реалізація моделі на ЕОМ сполучена з визначеними важкостями. Тому граф-модель частіше усього використовують як проміжну модель для побудови інших різновидів моделей.

Читайте також:

1. Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
2. Аналіз економічноїї політики за допомогою моделі Мандела-Флемінга. Випадки вільного та фіксованого валютного курсів.
3. Аналітичний підбір математичної моделі.
4. Бізнес-моделювання в системі управління розвитком підприємства. Поняття та етапи формування бізнес-моделі
5. Біографічні відомості
6. Біостратиграфічні методи визначення віку порід
7. Блок 1. Соціально-демографічні та міграційні процеси.
8. Великі географічні відкриття і первісне нагромадження капіталу
9. Великі географічні відкриття та їхній вплив на економічний розвиток Європи
10. Вибір підходу до процесу соціальної роботи зале­жить від теоретичної моделі, якої дотримуються соці­альні працівники, обраної стратегії втручання і методу соціальної роботи.
11. Види світогляду: міфологічний, релігійний та філософський (натуралістична, об’єктивно-ідеалістична, субєктивно-ідеалістичні і матеріалістичні моделі).
12. Використання моделі Хікса – Хансена для оцінки відносної ефективності бюджетно-податкової і кредитно-грошової політики

Переглядів: 938