• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Основні поняття

Векторні простори

Кондукторная втулка для сверления отверстий

Нормирование точности размеров гладких элементов деталей на технологических чертежах

Рассмотрим примеры оформления конструкторских (рис.33) и технологических чертежей (рис.34).

«Неуказанные предельные отклонения размеров: отверстий H14, валов h14, остальных ±»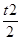

Рисунок 33 – Конструкторский чертеж

Рисунок 34 – Операционно–технологическая карта

а) Означення

Множина V елементів x, y, z,… називається лінійним, або векторним, простором, якщо сума х+у довільних двох її елементів х, у і добуток αхкожного її елемента хна будь-яке число α теж належать множині V, причому виконуються наступні умови:

1.

2.

3. 0– називають нульовим елементом.

4. –х називають елементом, протилежним до х.

y+x+z=y+(x+z)=y+0=yта

y+x+z=(y+x)+z=0+z=z

випливає y=z.

3. 0 · x = 0.

Дійсно, 0 · x = (0 + 0)x = 0 · x + 0 · x.Додавши до обох частин рівності - 0 · x , отримаємо 0 = 0 · x.

4.

Дійсно, Додавши до обох частин рівності отримаємо

5. Якщо добуток αх=0, то або α=0, або х=0.

Дійсно, якщо то

6. є протилежним до х.

Дійсно, х+(-1)х=1·х+(-1)х=[1+(-1)]x=0·x=0, звідки (-1)х= -х.

б) Розмірність і базис

Вектори а₁, а₂,…,а_k векторного простору V називаються лінійно залежними, якщо існують такі числа одночасно не рівні нулю, що

В іншому випадку вектори називають лінійно незалежними.

Якщо вектори а₁,а₂,…,а_kлінійно залежні, тобто , і, наприклад, то

тобто

де

Це означає, що вектор а_k є лінійною комбінацією решти векторів системи. Отже, якщо вектори а₁, а₂,…,а_k лінійно залежні, то, принаймні, один із них лінійно виражається через решту. Ясно, що справедливе і зворотнє твердження.

Максимальна кількість лінійно незалежних векторів системи векторів а₁, а₂,…,а_k називається рангом цієї системи. Позначають rank{ а₁, а₂,…,а_k}.

Довільна матриця містить дві системи векторів:

систему векторів – рядків {а₁,а₂,…,а_m} і систему векторів – стовпчиків

, де а_і=(а_і1,а_і2,…,а_іп), і=1,2,…,m, , j=1,2,…,n.

Ранг системи рядків довільної матриці А дорівнює рангу її стовпчиків і називається рангом матриці А. Позначається rankA або r(A).

Таким чином, для знаходження рангу матриці досить з допомогою елементарних перетворень над рядками (стовпчиками) звести її до ступінчастого вигляду і підрахувати кількість ненульових рядків (стовпчиків), яка й дорівнюватиме кількості лінійно незалежних серед них, а, отже, рангу матриці.

Приклад.

Знайти ранг матриці.

.

Розвязання.

Зведемо матрицю А до ступінчастого вигляду з допомогою елементарних перетворень її рядків:

Отже, r(A)=3.

Розмірністю векторного простору V називається максимальна кількість лінійно незалежних векторів, що містяться в ньому. Позначається dimV

(від dimage-фр).

Наприклад, розмірність множини всіх векторів площини дорівнює два, розмірність множини просторових векторів – три. Простори із скінченною розмірністю називаються скінченновимірними.

Базисом простору V називають впорядковану скінченну систему векторів, якщо:

1) вона лінійно незалежна;

2) кожний вектор простору V є лінійною комбінацією векторів цієї системи.

Коефіцієнти даної лінійної комбінації називаються компонентами або координатами вектора за цим базисом.

В заданому базисі компоненти вектора визначаються однозначно.

Дійсно, при двох заданнях вектора х в базисі а₁,а₂,…,а_k, зокрема, та , отримаємо Оскільки всі коефіцієнти (бо система а₁, а₂,…,а_k лінійно незалежна), то

В п-вимірному просторі кожна впорядкована лінійно незалежна система із п лінійно незалежних векторів є базисом. Ясно, що в п-вимірному просторі кожну впорядковану лінійно незалежну систему із k<n векторів можна доповнити до базису.

Розглянемо в просторі V два базиси: е=(е₁,е₂,…,е_п) та (перший з них назвемо старим, а другий – новим). Виразимо кожний вектор нового базису через вектори старого базису:

Можна сказати, що нові базисні вектори виражаються через старі з допомогою матриці

стовпчиками якої є коефіцієнти їх розкладу за векторами старого базису. Матриця А називається матрицею переходу від базису едо базису . Матриця переходу є невиродженою, оскільки в іншому випадку її стовпчики, а, отже, і вектори , були б лінійно залежними.

Розглянемо зв’язок між координатами одного і того ж вектора в старому і новому базисах.

Нехай х=х₁е₁+х₂е₂+…+х_пе_пі

Підставивiи замість їх вирази через е₁,е₂,…,е_п, отримаємо

Із єдиності розкладу вектора х за базисом е₁,е₂,…,е_п, випливає

звідки .

Таким чином, старі координати вектора отримуються із нових з допомогою тієї ж матриці А, тільки коефіцієнти відповідних розкладів утворюють тепер рядки цієї матриці.

Приклад.

Нехай е₁, е₂ – одиничні вектори, розташовані вздовж осей прямокутної декартової системи координат. Повернемо осі координат на кут φ проти годинникової стрілки і позначимо нові базисні вектори через та . Кути, утворені вектором з векторами е₁і е₂, рівні відповідно φ і

(див. малюнок). Тому координати цього вектора в базисі е₁, е₂ рівні і значить, . Аналогічно, кути вектора з векторами е₁ і е₂ рівні відповідно і φ, тому координати його в базисі

е₁, е₂ рівні і , значить,

e2     φ φ   e1

Таким чином, матриця переходу від базису е₁, е₂ до базису , матиме вигляд

Тоді старі координати виражаються через нові так:

звідки

в) Підпростори векторного простору

Підпростором векторного простору V називається сукупність V₁ його елементів, яка сама є векторним простором відносно введених в V операцій додавання і множення на число.

Для встановлення того, що деяка підмножина V₁ векторного простору V є його підпростором, досить показати, що для довільних двох векторів х та у із V₁ їх сума х+у теж належить V₁, і що для довільного вектора і довільного добуток теж належить V₁. Це твердження випливає із аксіом 1, 2, 5-8 векторного простору.

Приклади.

У звичайному тривимірному векторному просторі підпросторами є всі площини і всі прямі, які проходять через початок координат.

Сам простір V і множина із одного нульового елемента теж є підпросторами простору V (тривіальними).

Перетином двох підпросторів V₁ і V₂ векторного простору V називається множина всеможливих векторів із V, що належить одночасно і V₁, і V₂. Перетин теж є підпростором і позначається

Сумою двох підпросторів V₁ і V₂ називається множина векторів вигляду де Сума теж є підпростором і позначається V₁+V₂.

Теорема. Якщо V₁ і V₂ – підпростори векторного простору V, то

Доведення.

В підпросторі виберемо довільний базис е₁, е₂,…, е_k і доповнимо його до базису V₁ з одного боку:

е₁, е₂,…,е_k, f_k+1,…,f_p (*1)

і до базису V₂ з другого боку:

е₁, е₂,…,е_k, g_k+1,…,g_s (*2).

Покажемо , що вектори е₁, е₂,…,е_k, f_k+1,…, f_p, g_k+1,…,g_s лінійно незалежні.

Припустимо, що ці вектори лінійно залежні:

Тоді вектор

належить одночасно і V₁, і V₂, а, значить, і їх перетину Але тоді він повинен лінійно виражатись через базисні вектори підпростору :

тобто

.

Звідси і з єдиності розкладу вектора а за базисом простору V₁ маємо

Тоді матимемо

звідки, із лінійної незалежності базисних векторів простору V₂ маємо

Отже, вектори е₁, е₂,…,е_k, f_k+1,…, f_p, g_k+1,…,g_s утворюють лінійно незалежну систему. Але тоді вони утворюють базис простору V₁+ V₂, оскільки, якщо вектор то z=x+y, де і, значить, х лінійно виражається через (*1), а у – через (*2). Але тоді вектор z лінійно виражається через вектори

е₁, е₂,…, е_k, f_k+1,…, f_p, g_k+1,…,g_s.

Таким чином, розмірність підпростору V₁+ V₂ дорівнює

k+(p-k)+(s-k)=p+s-k.

Але dimV₁=p, dimV₂=s, Тоді

dimV₁+dimV₂=p+s і

що й треба довести.

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. II. Поняття соціального процесу.
3. V. Поняття та ознаки (характеристики) злочинності
4. А/. Поняття про судовий процес.
5. Адвокатура в Україні: основні завдання і функції
6. Адміністративний проступок: поняття, ознаки, види.
7. Адміністративні провадження: поняття, класифікація, стадії
8. Акти застосування юридичних норм: поняття, ознаки, види.
9. Амортизація основних засобів, основні методи амортизації
10. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
11. Артеріальний пульс, основні параметри
12. АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ

Переглядів: 532