• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Алгебраїчні системи

Сукупність множини М з заданими в ній операціями й відношеннями називають алгебраїчною системою.

Окремими випадками алгебраїчної системи є: решітка, модель, алгебра відношень, реляційна алгебра.

Моделлю називається сукупність множини М с заданими в ній відношеннями : ,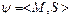

де множина М – носій моделі, S – сигнатура моделі, яка представляє собою множину відношень різної арності.

Алгеброю відношень називається сукупність множини відношень із заданими в ній операціями: об'єднання, перетинання, різниці й розширеного декартового добутку відношень.

Реляційна алгебра – це алгебра відношень з додатковими операціями над відношеннями: вибору, проекції, з'єднання.

Алгебра відношень і модель широко використовуються при формалізації реальних об'єктів, наприклад, при створенні інформаційного забезпечення - розробці реляційної бази даних.

Основою побудови реляційної бази даних є двовимірна таблиця, кожний стовпець якої відповідає домену ( або атрибуту, що відповідає частині домена ), рядок – кортежу значень атрибутів, що перебувають у відношенні R.

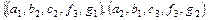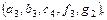
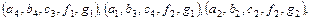
Приклад.Розглянемо 5-арное відношення R₅ : R₅ = , або .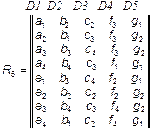

□ Дана таблиця визначає відношення реляційної моделі даних. Відношення R₅ є підмножиною декартового добутку доменов .

Елементами домена D_i служать значення атрибутів. Порядок стовпців у таблиці фіксований, рядки в загальному випадку можуть розташовуватися довільно.

Носій реляційної алгебри являє собою множину відношень, сигнатура крім уведених операцій (об'єднання, перетинання, різниця, і розширений декартовий добуток відношень ) включає спеціальні операції над відношеннями : вибір, проекцію, з'єднання.

Операція вибору являє собою процедуру побудови “горизонтальної“ підмножини відношення, тобто підмножини кортежів, що володіють заданою властивістю.

Для визначення проекцій відношень множина в реляційній алгебрі розбивається на дві підмножини у випадку бінарного відношення і на n підмножин у випадку n – арного відношення:

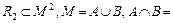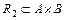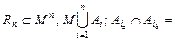Ø , ; Ø,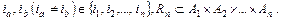

Проекцією Пр (R₂ / A) бінарних відношень R₂, R₂ , на А називають множину елементів Пр ( R₂ / A ) = =.

Проекцією Пр ( R_n / 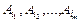) n – арного відношення на 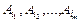називається множина кортежів , де , кожний з яких є частиною елемента n – арного відношення R_n .

Операція проекції визначає побудову “ вертикальної “ підмножини відношень, тобто множини підмножини кортежів, одержуваного вибором одних і виключенням інших доменов.

Операція з'єднання по двох таблицях, що має загальний домен, дозволяє побудувати одну таблицю, кожний рядок якої утвориться з'єднанням двох рядків вихідних таблиць. Із заданих таблиць беруть рядки, що містять одне й теж значення із загального домена; загальному домену зіставляється один стовпець.

Нехай потрібно визначити результати виконання операцій : 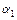- вибору по домену D₃ за значенням c₂ ; - проекції по домену D₅ ; - проекції по доменам D₂ , D₅ ; - з'єднання по домену D₁ для двох таблиць: перші чотири кортежі R₅ і другі чотири кортежі R₅ . Результати операцій будуть наступні :

; ;

;

.

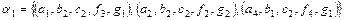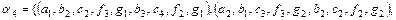
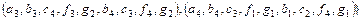Якщо відношення R₅ описує “іспити”, то значеннями атрибутів домена D₁ (a_i , i=) можуть бути шифри студентських груп; значеннями атрибутів домена D₂ (b_i , i=) – назви дисциплін; значеннями атрибутів домена D₃ (c_i , i=) – прізвища екзаменаторів; домена D₄ (f_i , i=) – дати іспитів; домена D₅ (g_i , i=1,2) – номера аудиторій.

Тоді результатом операції вибору 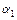є розклад іспитів екзаменатора с₂; результатом операції проекції - множина аудиторій; результатом операції проекції - множина пар, кожна з яких визначає дисципліну й аудиторію; результатом операції з'єднання - розклад іспитів кожної студентської групи.

Результати дії операцій 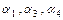є відношеннями, тобто не виводять із множини відношень. Результат операції проекції відношенням не є, тобто застосування даної операції виводить із множини відношень. ■

Запит у реляційній базі даних буде виконаний тим швидше, чим менше операцій над відношеннями він містить. Тому становить практичний інтерес задача зменшення числа цих операцій.

=============================== «» ===============================

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. POS-системи
8. VI. Філогенез нервової системи
9. Автокореляційна характеристика системи
10. АВТОМАТИЗОВАНІ СИСТЕМИ ДИСПЕТЧЕРСЬКОГО УПРАВЛІННЯ
11. АВТОМАТИЗОВАНІ СИСТЕМИ УПРАВЛІННЯ ДОРОЖНІМ РУХОМ
12. Автоматизовані форми та системи обліку.

Переглядів: 2012