
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Основа теорії похибок. Поняття значущості, довірчого інтервалу і довірчої вірогідності.
Принципові підходи до визначення залежностей показників якості харчових продуктів в умовах неможливості побудови їх опису на основі фундаментальних фізичних законів процесів перенесення.
И1 110-127 вибірково
У процесах, пов'язаних з перенесенням імпульсу механічної енергії, теплової енергії, а також маси, повний (найбільш загальне) математичний їх опис представляється в рівняннях математичної фізики (диференціальні рівняння в приватних похідних для нестаціонарного тривимірного процесу), які не мають загального аналітичного рішення.
Використовуючи основні положення теорії подібності, можна визначити умови, при яких ці рівняння можуть бути замінені критерійними співвідношеннями, для чого здійснюється перехід до безрозмірних параметрів, формулюються нові граничні і початкові умови, а також заздалегідь передбачається форма критерійного співвідношення. Проте, як відомо, отримати рівняння в узагальнених змінних можна тільки використовуючи результати експерименту.
В цьому випадку теорії подібності виступають як теорія експерименту, оскільки вона визначає: які величини підлягають зміні, в яких діапазонах повинні змінюватися абсолютні значення вимірюваних величин, і, оскільки форма критерійного співвідношення обгрунтовано відома, також відомі вимоги до обробки результатів експерименту.
И1 110-113, И1 128-133, И1 136-142,
Моя книга по метрологи
Основна задача теорії похибок – знаходження області невизначеності результату.
Похибка вимірювання - це відхилення результату вимірювання від істинного значення вимірюваної фізичної величини.
Джерелами похибок (помилок) при виконанні інженерних розрахунків та обчислень з використанням ЕОМ можуть бути:
1. Неточне відображення реальних процесів за допомогою математики.
2. Наближене значення величин, які входять в умову задачі, внаслідок їх неточного виміру.
3. Заміна нескінчених процесів, межами яких є шукані величини, кінцевою послідовністю дій.
4. Округлення вхідних даних, проміжних або кінцевих результатів.
5. Крім вказаних вище випадків, похибки можуть з’являтися в результаті дій над наближеними числами.
За джерелами виникнення похибки подіяють на:
- Методична — складова похибки вимірювання, обумовлена недосконалістю методу вимірювання або невідповідністю об'єкта вимірювання його моделі, прийнятій для вимірювання.
- Інструментальна – складова похибки вимірювання, обумовлена властивостями засобу вимірювання. Ця похибка в свою чергу може містити кілька компонентів, зокрема, похибку засобу вимірювання та похибку обумовлену взаємодією засобу вимірювання з об'єктом вимірювання.
- Суб’єктивна (Похибка оператора) – складова похибки вимірювання, обумовлена індивідуальними властивостями оператора.
За формою або способом відображення кількісної оцінки:

 1. Абсолютна похибка – це різниця між результатом вимірювання x шуканої величини і її дійсним значенням х (або реалізацією в даному вимірюванні), виражена в одиницях вимірювання:
1. Абсолютна похибка – це різниця між результатом вимірювання x шуканої величини і її дійсним значенням х (або реалізацією в даному вимірюванні), виражена в одиницях вимірювання:
| Δν = х – ν | (16) |
де х – результат вимірювання; х – дійсне значення.
2. Відносною похибкою називають погрішність, що доводиться на одиницю вимірюваної величини. Її зазвичай виражають у відсотках
| δ = (Δν/ν) 100% | (17) |
За закономірністю або характером змінювання:
1. Випадкова – складова загальної похибки вимірювання, яка змінюється випадковим чином (як за знаком, так і за величиною) під час повторних вимірювань однієї і тієї ж величини.
2. Систематична – складова загальної похибки вимірювання, яка залишається постійною або закономірно змінюється під час повторних вимірювань однієї і тієї ж величини.
Повна похибка є результатом складної взаємодії всіх видів похибок.
Абсолютна похибка функції визначається як сума абсолютних похибок параметрів функції помножених на вагові коефіцієнти, які характеризують швидкість зміни функції при зміні кожного параметра (модуль часткової похідної функції по відповідному параметру). Відносна похибка може бути визначена сумою абсолютних похибок параметрів функції помножених на вагові коефіцієнти, які представляють собою модуль часткової похідної логарифма функції по відповідному параметру.
Якщо функція являє собою суму параметрів, то абсолютна похибка теж є сумою похибок.
Якщо функція представляє собою добуток параметрів, то і відносна похибка також представляє добуток.
Наближеним числом називають число а, яке несуттєво відрізняється від точного числа А і заміняє останнє при обчисленнях.
Значущими цифрами наближеного числа а називаються всі цифри в його десятковому зображенні, відмінні від нуля, та нулі, якщо вони є між значущими цифрами або розміщені в кінці числа і вказують на збереження розряду точності. Нулі, що стоять лівіше першої відмінної від нуля цифри, не є значущими цифрами. Наближене число а має n дійсних значущих чисел у вузькому смислі, якщо абсолютна похибка цього числа не перевищує половини одиниці десяткового розряду, який виражається n-значущою цифрою, читаючи зліва направо; тобто якщо виконується рівність:
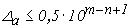
| (18) |
Якщо ця нерівність не виконується, то цифру 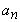 називають сумнівною. Очевидно, що якщо цифра
називають сумнівною. Очевидно, що якщо цифра 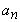 - дійсна, то і всі попередні цифри також вірні.
- дійсна, то і всі попередні цифри також вірні.
Таким чином, серед дійсних цифр завжди можна вказати останню. Наближене число:
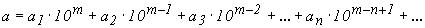
| (19) |
містить n вірних значущих цифр в широкому смислі, якщо абсолютна похибка цього числа не перевищує одиниці десяткового розряду, який виражається n значущою цифрою, якщо виконується нерівність
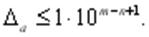
| (20) |
Для повного уявлення про точність вимірювань та надійність оцінки випадкових відхилень результатів вимірювань, особливо при обмеженій кількості значень вимірюваної величини, необхідно задатися довірчими межами, довірчим інтервалом та довірчою ймовірністю. Для визначення точності оцінки  в математиці користуються довірчими інтервалами, а для визначення надійності – довірчою імовірністю. Розкриємо суть цих понять. Нехай для параметра а отримана з випробування незміщена оцінка
в математиці користуються довірчими інтервалами, а для визначення надійності – довірчою імовірністю. Розкриємо суть цих понять. Нехай для параметра а отримана з випробування незміщена оцінка  . Потрібно оцінити можливу при цьому помилку. Задаємо деяку вірогідність β (наприклад β=0,9) і знайдемо таке значення ξ >0, для якого
. Потрібно оцінити можливу при цьому помилку. Задаємо деяку вірогідність β (наприклад β=0,9) і знайдемо таке значення ξ >0, для якого  . Або ще можна записати так:
. Або ще можна записати так: 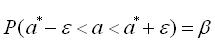 . Остання рівність означає, що невідоме значення параметра а з імовірністю β потрапить в інтервал
. Остання рівність означає, що невідоме значення параметра а з імовірністю β потрапить в інтервал 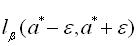 . Тут невідоме значення параметра а є невипадковою величиною, а інтервал
. Тут невідоме значення параметра а є невипадковою величиною, а інтервал  є випадковою величиною, оскільки положення інтервалу на осі залежить від випадкової величини
є випадковою величиною, оскільки положення інтервалу на осі залежить від випадкової величини  (центр інтервалу). Тому вказана вище імовірність трактується як імовірність того, що випадковий інтервал
(центр інтервалу). Тому вказана вище імовірність трактується як імовірність того, що випадковий інтервал  накриє точку а.
накриє точку а.
Інтервал  називається довірчим інтервалом, а імовірність β – довірчою імовірністю або надійністю β,що відповідає даному довірчому інтервалу
називається довірчим інтервалом, а імовірність β – довірчою імовірністю або надійністю β,що відповідає даному довірчому інтервалу  .
.
При обробці результатів експериментів виникає необхідність оцінки характеристик випадкової величини. В якості оцінки 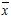 невідомого математичного сподівання
невідомого математичного сподівання 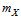 випадкової величини
випадкової величини 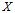 використовується середнє арифметичне результатів
використовується середнє арифметичне результатів 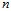 незалежних випробувань
незалежних випробувань
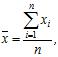
а для оцінки дисперсії 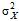 - співвідношення
- співвідношення

При припущенні нормального закону розподілу величини  можна показати, що величина
можна показати, що величина
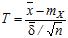
| (21) |
має t-розподіл Стьюдента з 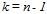 ступенями вільності. Звідси можна визначити надійний інтервал для справжнього значення
ступенями вільності. Звідси можна визначити надійний інтервал для справжнього значення 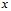 : за відомими значеннями надійної імовірності
: за відомими значеннями надійної імовірності 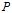 з таблиць знаходимо
з таблиць знаходимо 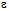 , звідки
, звідки
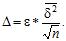
| (22) |
Таким чином, випадкова величина 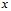 розподілена за нормальним законом з математичним сподіванням
розподілена за нормальним законом з математичним сподіванням 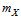 і дисперсією
і дисперсією 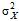 . Справжнє значення
. Справжнє значення 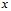 знаходиться в інтервалі
знаходиться в інтервалі 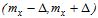 з надійною імовірністю
з надійною імовірністю 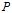 .
.
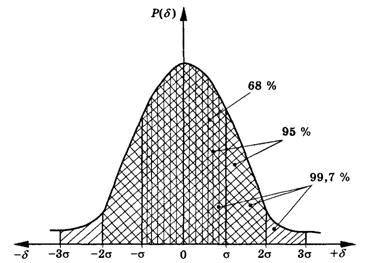
Додати опис 3сигм для нормального закону розподілення.
Для звичайних технічних вимірювань, коли не вимагається високий ступінь надійності та точності, довірча ймовірність береться у межах 0,9—0,95. Виходячи з нормального закону розподілу, можна розраховувати ймовірність виникнення випадкових похибок з різними значеннями. Рівень довіри РД означає, що правило визначення інтервалу дає вірний результат з імовірністю РД, що звичайно вибирається близькою до 1, однак, 1 не дорівнює.
Читайте також:
- II. Поняття соціального процесу.
- Nom. sing. Gen. sing. Основа
- V. Поняття та ознаки (характеристики) злочинності
- А .Маршалл - основоположник неокласичної теорії.
- А/. Поняття про судовий процес.
- Адміністративний проступок: поняття, ознаки, види.
- Адміністративні провадження: поняття, класифікація, стадії
- Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
- Акти застосування юридичних норм: поняття, ознаки, види.
- Альтернативні теорії вартості
- Альтернативні теорії капіталу
- Альтернативні теорії макроекономічного регулювання
| <== попередня сторінка | | | наступна сторінка ==> |
| Критерії подібності і їх фізичний сенс. | | | Розрахунок гдравлічних опорів апаратів. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |