Основні методи оптимізації.

И1 290-303

Найпростішим методом рішення задачі є перебір усіх варіантів. Для того щоб установити найкращий варіант, переглядають усі можливі умови ведення технологічного процесу при всіх можливих чи доцільних логічних значеннях вхідних параметрів процесу. Цей метод використовують при обмеженому числі чи варіантів при порівняно нескладних обчислювальних процедурах. Практично цей метод є нереальним, тому що нескінченне число припустимих варіантів неможливо перебрати протягом доступного для огляду проміжку часу. Для вибору найкращих рішень часто користаються інтуїтивними методами, заснованими на досвіді і кваліфікації фахівців. Отримані таким способом рішення можливі для порівняно простих задач, вони не гарантують оптимального рішення і доступні дуже обмеженому колу фахівців.

У тому випадку, якщо відома функціональна залежність критерію оптимальності R від перемінної стану х., те можна безпосередньо обчислити його значення для деякого фіксованого значення цієї перемінної. Надалі, змінюючи значення перемінної, можна обчислювати критерії доти, поки його значення буде зростати при пошуку максимуму і зменшуватися при пошуку мінімуму. Задачі на максимум і мінімум можуть бути вирішені також класичними методами диференціального числення, що використовуються у випадку одного перемінної чи стану декількох перемінних з невеликим діапазоном зміни. При великій області зміни перемінних і наявності більш ніж одного экстремума досліджуваної функції використання цих методів не ефективно.

Якщо функція однієї перемінної безупинна і дифференцируема і має роцес со у будь-якій не крайній крапці діапазону зміни цієї перемінний, то в цій крапці повинне виконуватися умова

─── ==0.

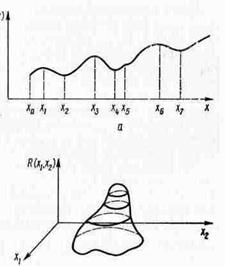
З графіка такої функції, приведеного на роц. A, видно, що ця умова є лише необхідним., Функція має максимуми в крапках Х₁, Х₃, Х₆ і мінімуми в крапках Х₂, Х₄, Х₇ . Однак у цих крапках значення функцій не є ні найбільшими, ні найменшими. Найбільший з максимумів і найменший з мінімумів іноді називають абсолютним, чи глобальним, а всі інші — відносними. Відшукуючи абсолютний чи мінімум максимум рішенням останнього рівняння, можна знайти відносний чи мінімум максимум. Якщо найменше значення функції R (х,у) досягається в крапці, що лежить на границі діапазону зміни перемінної Х, то аналітично це значення визначити неможливо.

Для безупинної і дифференцируемой функції п перемінних R (х₁, х₂, …, х_n) необхідна умова існування відносного экстремума в крапках х₁, х_2…полягає в тому, що всі частки похідні дорівнюють нулю в цій крапці

Поклавши частки похідні R (x_i) рівними нулю і вирішивши п рівнянь, можна знайти значення R, що дають стаціонарне значення критерію оптимальності. Для встановлення чи максимуму мінімуму необхідно досліджувати старші похідні. Це справедливо тільки у випадку, якщо функція має єдиний локальний роцес со.

Метод множників лагранжа.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Схеми розрахунку сушарок	\|	Об'єкт і предмет конфліктології

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.02 сек.