
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
В умовах конкуренції
Модель зростання випуску продукції
Припустимо, що деяка фірма випускає продукцію й продає її за ціною  за одиницю. Позначимо через
за одиницю. Позначимо через  обсяг продукції, яка реалізована в момент часу
обсяг продукції, яка реалізована в момент часу 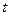 . Нехай ціна залежить від обсягу продукції. Тоді
. Нехай ціна залежить від обсягу продукції. Тоді  - спадна функція, тобто зі збільшенням обсягу випуску продукції її ціна на ринку зменшується. Це означає, що
- спадна функція, тобто зі збільшенням обсягу випуску продукції її ціна на ринку зменшується. Це означає, що  У момент часу
У момент часу 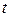 фірма одержує доход
фірма одержує доход  . Якщо частина доходу використовується на інвестиції
. Якщо частина доходу використовується на інвестиції 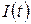 у виробництво реалізованої продукції, то за умови не насиченості ринку швидкість випуску продукції пропорційна збільшенню інвестицій, тобто
у виробництво реалізованої продукції, то за умови не насиченості ринку швидкість випуску продукції пропорційна збільшенню інвестицій, тобто  , де
, де  - це норма інвестицій,
- це норма інвестицій,  - норма акселерації,
- норма акселерації,  - стала ціна.
- стала ціна.
У випадку, коли ціна  , дістанемо диференціальне рівняння першого порядку відносно
, дістанемо диференціальне рівняння першого порядку відносно  із відокремленими змінними
із відокремленими змінними
 , (7)
, (7)
де  . Оскільки всі співмножники в правій частині цього рівняння додатні, то й
. Оскільки всі співмножники в правій частині цього рівняння додатні, то й  , тобто функція
, тобто функція  зростаюча. Характер зростання функції визначається її другою похідною. Диференціюючи рівняння (7), дістанемо
зростаюча. Характер зростання функції визначається її другою похідною. Диференціюючи рівняння (7), дістанемо
 (8)
(8)
Оскільки еластичність попиту  , то рівність (8) можна записати у вигляді
, то рівність (8) можна записати у вигляді
 .
.
Ураховуючи, що 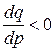 , а отже, й
, а отже, й 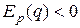 , остаточно дістанемо
, остаточно дістанемо
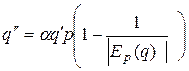 . (9)
. (9)
Із рівності (12.58) випливає, що за еластичного попиту, тобто коли 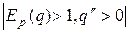 , графік функції
, графік функції  має напрям опуклості вниз, а це означає прогресивне зростання; за нееластичного попиту, тобто при
має напрям опуклості вниз, а це означає прогресивне зростання; за нееластичного попиту, тобто при 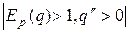 , графік функції
, графік функції  має напрям опуклості вгору, що означає вповільнене зростання (насичення).
має напрям опуклості вгору, що означає вповільнене зростання (насичення).
Розглянемо залежність ціни від попиту  у вигляді лінійної функції
у вигляді лінійної функції
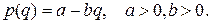 (10)
(10)
Тоді рівняння (7) і (9) набирають вигляду
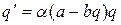 (11)
(11)
І
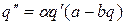 (12)
(12)
Відповідно.
Зі співвідношень (11) і (12) дістанемо, що  при
при 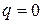 і
і 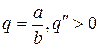 при
при  при
при  . Отже,
. Отже, 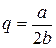 - точка перегину графіка функції
- точка перегину графіка функції  .
.
Графік функції  - однієї з інтегральних кривих диференціального рівняння – називають логістичною кривою.
- однієї з інтегральних кривих диференціального рівняння – називають логістичною кривою.
Читайте також:
- H) Орган з питань конкуренції
- Адміністративний захист об’єктів інтелектуальної власності від недобросовісної конкуренції
- Актуальність і завдання курсу безпека життєдіяльності. 1.1. Проблема безпеки людини в сучасних умовах.
- Аналіз та оцінка інвестування в умовах ризику. Якісні та кількісні методи оцінювання проектних ризиків.
- Аналітична робота в умовах кризи.
- Антипод конкуренції.
- АТ – одна з найбільш зручних форм колективного підприємства в умовах ринкової економіки. Першим АТ вважають створену у 1602 році Голандсько –Ост - Індську компанію.
- Безпека в умовах кримінальної злочинності
- Безпека життєдіяльності людини в умовах натовпу
- Бетонування в зимових умовах
- Більш повну практику ціноутворення в сучасних умовах у розвинутих країнах світу допоможе з’ясувати короткий виклад розвитку теорії ціни.
- В сучасних умовах
| <== попередня сторінка | | | наступна сторінка ==> |
| Випуску продукції | | | Природа лідерства в соціальному середовищі та основні ознаки |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |