• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розрахунок

Ланок

Таблиця 1

Розрахунок методом повної взаємозамінності

ланка	Ном. р-р	Одиниця допуску	Поле допуску	Допуск мкм	Верх.відх	Нижн.	Коорд.середини поля допуску
А1   А2   А3   А4   А5 А6     А7   А8   АD	5,5   0,5	2,90   0,73   -   1,56   1,31   2,17     -   0,73   -	h8   js9   (h)   h9   js9 h8   (h)   js9   (js)	-	-     +43,5     +15   +300	-72   -15   -150   -   -52   -43,5 -54   -120   -15   -300	-36     -75   -   -26   -27   -60

3. По ГОСТ 25346 –89 визначаємо одиницю допуску i і заносимо їх в табл. 2.1, для всіх ланок окрім А_D , А₃ и А₇ /подш./

4. Визначаємо розрахункову кількість одиниць допуску

Т_D - åТ_n 600 – ( 150 + 120 )

а= = = 35.1 ,

åI_j 2.9+0.73+1.56+1.31+2.17+0.73

де n – кількість ланок без А_D, А₃ і А₇ /підш/.

5. Встановимо між якими квалітетами знаходиться розрахункове значення По ГОСТ 25346-89 а=25 для квалітета 8 і а=40 для 9 квалітета. Для тих ланок на які більш легко отримати високу точність призначимо допуски по 8 квалітету, а для інших по 9

квалітету. Основні відхилення для поверхонь, що охоплюються – по h, а для виступу кришки js. Заносимо в таблицю.

Примітка . Якщо ( Т_D - åТп ) £ 0, то ця задача не вирішується методом повної взаємозамінності.

6. Визначаємо допуск ув’язувальної ланки ТА₄ і з умови

Т_D=åТ_i ;

600 = 72 + 30 + 150 + 52 + 54 + 120 + 30 + ТА₄ ;

ТА₄ = 92 мкм .

7. Перевіряється чи знаходиться допуск ланки А₄ (ТА₄ = 92) між 8 і 9 квалітетами

IТ8 = 39 мкм;

IT9 = 62 мкм;

тобто ТА₄ > IТ9, в цьому випадку необхідно збільшити допуск одного або 2-х складових ланок, щоб IT8 £ TA₄ £ IT9.

Збільшуємо поле допуску ланки А₆ Þ h9 – нове значення.

8.Перераховуємо допуск ув’язувальної ланки

600 = 72+30+150+52+87+120+30+ТА₄ ;

ТА = 59 мм .

Допуск ТА₄ знаходиться між допусками по 8 і 9 квалітетам.

Заносимо в таблицю значення ТА₄.

9. Визначаємо координату середини поля допуску ув’язувальної ланки з формули:

E_D=åEc_i ;

Еc_D=0 –для нашого випадку;

0=(+1)(-36) + (-1) [ -0 –75 –26 – 0 – 60 - 0 ] + (-1) Ес₄ .

Ес₄= +125мкм(Заносимо в таблицю).

10.Граничні відхилення ув’язувальної ланки

ЕS₄ = Еc₄ + T₄ / 2 = 125 +59 / 2 = 154,5 мкм ;

ЕI₄ = Еc₄ – T₄ / 2 = 125 – 59 / 2 = 95,5 мкм ;

Заносимо в таблицу

ув’язувальна ланка _+0.155

A₄ = 40_+0.096

Імовірнісний метод розрахунку розмірних ланцюгів

При розрахунку ланцюгів на mаx – min ми передбачали, що в процесі обробки або збирання можливе одночасне поєднання найбільших збільшувальних і найменших зменшувальних розмірів або зворотне їх поєднання. Внаслідок цього розмір замикаючої ланки отримає або максимальне або мінімальне значення. Такий випадок можливий, але імовірність йогоздійснення дуже мала.

У зв’язку з цим цей метод приводить до необгрунтованої жорсткості допусків, особливо при великій кількості ланок ( n >4).

Більш точним і науково-обгрунтованим методом розрахунку розмірних ланцюгів є метод, заснований на теорії імовірностей.

Вважаємо, що погрішності складових ланок (розміри механічно оброблених деталей) підкоряються закону нормального розподілу. У одній з теорем теорії імовірності доводиться, що якщо випадкова величина являє собою суму великого числа взаємно незалежних випадкових доданків, серед яких немає домінуючих по своїй величині, то незалежно від того, яким законам розподілу підкоряються доданки, сума завжди буде мати розподіл близький до нормального, і тим точніше, при більшій кількості доданків.

Тому погрішності замикаючой ланки будуть підкорятися закону нормального розподілу і тим точніше при більшій кількості складових ланок розмірного ланцюга ( n > 5).

Закон нормального розподілу виражається рівнянням

y(x)=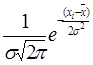 (2.13)

де у(х) –щільність імовірності,

s - середнє квадратичне відхилення випадкової величини;

Х _і – випадкова величина неперервного типу;

Х – середнє арифметичне значення випадкової величини;

s²- дисперсія випадкової величини

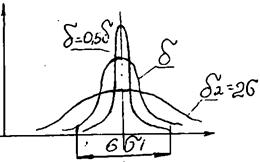
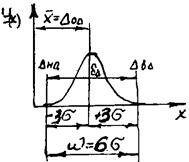
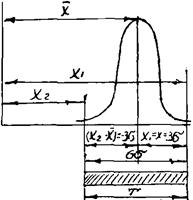
Закон нормального розподілу характеризується двома параметрами s іx.Параметр s є мірою розсіювання випадкової величини х, із збільшення s крива стає більш пологою.

А параметр хє мірою положення кривої відносно осі ординат.

Закон нормального розподілу звичайно застосовується y безрозмірному вигляді, для цього (X _і – X) виражається в долях s і позначається через t

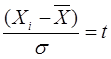- нормований параметр розподілу. (2.14)

Якщо прийняти межі імовірного розподілу (X_1,2 –) = ± 3s, отже величину поля розсіяння w =6s , і прирівняти поле розсіяння допуску Т то отримаємо

T_AD=6s_AD ; s_D=T_D/6 ; (2.15)

T_Ai=6s_Ai ; s_i=T_i/6 . (2.16)

При цьому імовірність появи браку не перевищує 0,27%.

З теорії імовірності відомо, що дисперсія суми випадкових величин рівна сумі дисперсій цих доданків:

_n

s_D² = ås_{i .} (2.17)

ⁱ⁼¹

Звідси

s_D =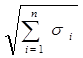 .(2.18)

Так як крива симетрична відносно центра розсіяння то межа поля розсіяння

(X_1,2 -) = Т/2 , (2.19)

і величину t з вираження (2.14)можна записати

t_Δ = та 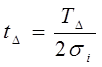(2.20)

де t_D - коефіцієнт ризику.

З виразів (2.18) і (2.20) отримаємо

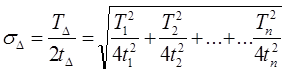(2.21)

Позначимо 1/t_i =l_i (2.22)

і назвемо l_I коефіцієнт відносного розсіювання.

Підставивши (2.22) в рівняння (2.21) отримаємо

s_D=(2.23)

Прирівняємо s_D= і отримаємо

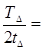
(2.24)

Підставимо Т = а× i в рівняння (2.24) і отримаємо

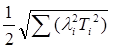(2.25)

Звідси кількість одиниць допуску

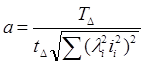(2.26)

Коефіцієнт ризику t_D призначається в залежності від допустимого відсотку браку на виробництві (при складанні). При цьому для замикаючої ланки застосовується нормальний закон розподілу при t =3 допустимий відсоток браку складає 0,27%.

Коефіцієнт відносного розсіювання

li²=1/9 - для закону нормального розподілу;

li²=1/6 - для закону розподілу трикутника;

li²=1/3 - для закону рівної імовірності.

{У окремій літературі li² означається як l ¹}

У розрахунках застосовується також Кi -коэфициент відносного розсіювання.

Цей коефіцієнт характеризує міру відмінності розподілу погрішностей iї ланки від нормального розподілу, якому звичайно підкоряються похибці замикаючої ланки.

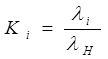(2.27)

- для закону нормального розподілу,

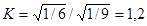- для закону розподілу трикутника,

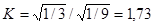- для закона рівної імовірності.

Введемо коефіцієнт відносного розсіювання К. Тоді рівняння (2.24), (2.25) і (2.26) запишуться так

T_D =; (2.28)

T_D = 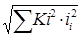; (2.29)

a =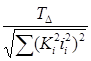(2.30)

^.

Для достовірного розрахунку необхідно визначити експериментальні закони розподілу для складових ланок.

Якщо їх немає то, в більшості випадків, рекомендується застосовувати для складових ланок (серійне виробництво) l ²_i= 1/6.

При t=3 и l_i² = 1/9

a =. (2.31)

При t=3 и l _i = 1/6

a=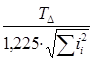(2.32)

Значення а при l = 1/6 виходить в 1,225 рази менше а при l_i = 1/9, тобто забезпечується запас точності.

Якщо допуск яких-небудь ланок відомий (наприклад підшипників) то

а=(2.33)

Якщо для підшипника прийняти l_i = 1/9 і t_D = 3 (масове виробництво) то

a =(2.34)

Імовірностний метод для розмірних ланцюгів з малою кількістю

Застосовується для ланцюгів з числом складових ланок n < 5(наприкладдля розрахунку ланцюгів з векторними помилками).)

При n < 5похибки замикаючої ланки не підкоряються закону нормального розподілу, тому вводять коефіцієнт К_D или l_D² також і на допуск замикаючої ланки Т_{D .} У зв'язку з цим формули (2.24) і (2.28) приймуть вигляд

T_D =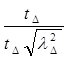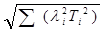(2.35)

T_D =(2.36)

Коефіцієнт К_D визначається по емпіричній формулі (в проектних умовах Кi=1,2))

K_D =1+ (2.37)

По отриманому значенню К_D можна визначити коефіцієнт l_D²

Приклад: Ланцюг складається з 3-х ланок Т₁=0,4 мм, Т₂=0,2 мм, Т₃=0,1 мм

К_D= 1 +;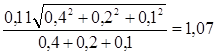

Т_D =(1/1,07)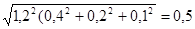

Приклад розрахунку розмірного ланцюга методом неповної взаємозамінності (імовірносним методом)

Проектний розрахунок (пряма задача)

Рисунок і умови задачі (див. 1)

Пункти 1-3 виконуємо в тій же послідовності і в тому ж об'ємі, що і для розрахунку імовірносним методом. Додатково в п.З визначаємо значення i ² (приводиться в методичних вказівках з курсового проектування) і також заносимо його в таблицю 2.2

Читайте також:

1. Автоматичний розрахунок суми проведення.
2. Аеродинамічний розрахунок
3. Аеродинамічний розрахунок ротора вітроустановки
4. Аналітичний розрахунок завантаження горловин
5. Аналітичний розрахунок сумарного завантаження типових перетинань
6. Види норм праці, їх розрахунок
7. Вплив характеру кола на криву струму при несинусоїдній напрузі /розрахунок найпростіших кіл
8. Гідравлічний розрахунок
9. Гідравлічний розрахунок малих мостів
10. Гідравлічний розрахунок сифонів
11. Графічний розрахунок режиму роботи ПСН
12. Графоаналітичний розрахунок витрат тепла і повітря на сушіння.

Переглядів: 794