• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Переведення дробових чисел з однієї системи числення до іншої

Нехай задане М-кове дробове число V, (0≤V≤1). Припустимо, що у N-ковій системі числення число V має запис V=(0,х_-1ї_-2)_N, тобто

Тут цифри х_-і невідомі. Помножимо обидві частини рівності на N:

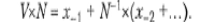
Значення цифри х_-1 отримаємо, взявши цілу частину добутку V×N, тобто

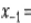
позначають цілу та дробову

частини V×N. Помножимо дробову частину {V×N} на N i знову візьмемо цілу частину. В результаті отримаємо значення цифри х_-2 і т. д. Якщо на деякій ітерації значення {V×N} стане рівним 0, процес можна припинити. Але, можливо, значення {V×N} ніколи нулю не дорівнюватиме. В такому разі запис точного значення V у N-ковій системі буде нескінченним, а кожна додатково отримана цифра уточнюватиме наближене значення V.

Отже, для переведення дробу з М-кової системи числення до N-кової потрібно послідовно множити дробову частину на основу системи числення N. Цілі частини добутків, отриманих у результаті виконання послідовності операцій множення, є цифрами дробу в N-ковій системі числення.

У разі, коли V задане у вигляді скінченного десяткового дробу і число N має серед своїх простих дільників як 2, так 1 5, зображення числа V в N-ковій системі числення буде скінченним. Інакше в N-ковій системі числення десятковий дріб V може зображуватися нескінченним періодичним дробом.

Приклад1.4 ________________________________________________________

Нехай потрібно перевести десятковий дріб 0,75 до двійкової системи. Послідовність операцій множення така: 0,75×2 = 1,5; ціла частина |_I,5_| = 1, дробова частина {1,5} = 0,5; 0,5×2 = 1, дробова частина {1} = 0. Усі подальші цифри будуть нулями, тому 0,11₂ є скінченним двійковим зображенням дробу 0,75₁₀.

У процесі переведення десяткового дробу 0,26₁₀ у двійкову систему виконується така послідовність операцій множення: |_0,26×2_|=|_0,52_|=0; |_0,52×2_|=|_1,04_|=1; |_0,04×2_|=|_0,08_|=0; |_0,08×2_|=|_0,16_|=0; |_0,16×2_|=|_0,32_|=0; |_0,32×2_|=|_0,64_|=0, |_0,64×2_|=1. Точне двійкове зображення десяткового дробу 0,26 є нескінченним періодичним, a 0,010 000 1₂ - його наближення.

Переведення десяткового дробу 0,8 у шістнадцяткову систему числення здійснюється так: 0,8×16 = 12,8 з цілою частиною |_12,8_|=12 і дробовою частиною {12,8} = 0,8. Десяткове число 12 замінюємо на шістнадцяткове значення С₁₆. Усі подальші шістнадцяткові цифри будуть також дорівнювати С. Отже, маємо періодичний дріб 0,(С)₁₆.

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. N – чисельність популяції
8. POS-системи
9. VI. Філогенез нервової системи
10. А. Це наявність в однієї людини кількох ліній клітин з різним набором хромосом.
11. Автододавання та автообчислення.
12. Автокореляційна характеристика системи

Переглядів: 3427