• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник

Переведення натуральних чисел з однієї системи числення до іншої

Розглянемо задачу переведення числа Р з М-кової системи числення до N-кової. Нехай число Р у N-ковій системі числення має запис Р=(х_кх_к-1…х₁х₀)_N який містить цифри х_і у невідомій кількості k+1. Записати це число можна так:

Звідси видно, що значенням наймолодшої цифри д:0 є остача від ділення числа Р на основу N (усі операції здійснюються над М-ковими числами). Значенням другої справа цифри х₁ буде остача від ділення частки, яку отримано на попередній ітерації, на основу N. Продовжуючи ці міркування, отримаємо циклічну процедуру, кожна ітерація якої полягатиме у знаходженні частки та остачі від ділення деякого числа Q на основу системи числення. При цьому отримана на і-й ітерації частка стає самим числом Q на (і+1)-й ітерації. Якщо частка менша від N, обчислення завершують. Остання частка є старшою цифрою числа, інші цифри записуються в порядку, зворотному до порядку отримання остач, тобто перша остача дає наймолодшу цифру.

Приклад 1.3 _______________________________________________________

Нехай потрібно перевести число 2510 з десяткової системи числення до двійкової. Для розв'язання цієї задачі застосуємо щойно описану схему обчислень. Остачу від ділення будемо записувати в дужках після частки.

25 : 2 = 12(1);

12: 2= 6(0);

6 : 2= 3(0);

3 : 2= 1(1).

Остання частка менша двох. Вона є старшою цифрою двійкового числа, до якого треба дописати остачі у порядку, зворотному до порядку їх отримання. Результатом є число 11001₂.

3 математичної точки зору переведення чисел з будь-якої М-кової позиційної системи числення до будь-якої N-кової здійснюється за тією процедурою, що її було розглянуто вище. Проте в цій процедурі операції знаходження частки та остачі від ділення здійснюються над числами у М-ковій системі, а для людини звичними є лише операції над десятковими числами. Тому, як зазначалося вище, десяткове значення М-кового числа Р зручніше обчислювати, користуючись його зображенням у вигляді поліному

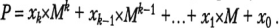
Наприклад:

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. N – чисельність популяції
8. POS-системи
9. VI. Філогенез нервової системи
10. А. Це наявність в однієї людини кількох ліній клітин з різним набором хромосом.
11. Автододавання та автообчислення.
12. Автокореляційна характеристика системи

Переглядів: 503