• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Поняття про втрату стійкості при напруженнях, що перевищують границю пропорційності

Виведення формули Ейлера ґрунтується на застосуванні диференціаль­ного рівняння пружної лінії. Тому скористатися цією формулою можна лише тоді, коли справедливий закон Гука, тобто доки критичне напруження (напруження стискання, що відповідає критичній силі) не переви­щує границі пропорційності:

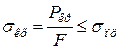. (4.5)

Виведемо формулу для критичного напруження σ_кр. Відповідно до виразів (4.5) та (4.4)

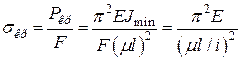. (4.6)

Тут 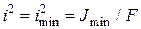– квадрат найменшого з головних радіусів інерції стрижня; F = F_бр – площа брутто поперечного перерізу стрижня. Ввівши безрозмірну величину

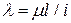, (4.7)

що називається гнучкістю стрижня (slenderness ration of a bar), остаточно знайдемо

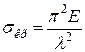, (4.8)

тобто критичне напруження стрижня залежить тільки від пружних властивостей матеріалу (модуля пружності Е) та гнучкості стрижня λ.

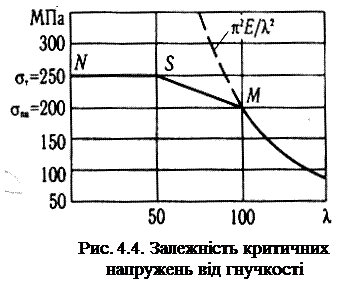Функціональна залежність (4.8) становить видозміну формули Ейлера. У системі координат σ_кр ≈ λ цю залежність можна подати у вигля­ді гіперболічної кривої, що зветься гіперболою Ейлера. Як приклад наведе­мо такий графік (рис. 4.4) для стрижня зі сталі марки Ст. 3, для якої модуль пружності Е = 2,1 ∙ 10⁵ МПа, границя текучості σ_т = 240 МПа, а границя пропорційності σ_пц = 200 МПа. Графік показує, що в міру зростання гнучкості стрижня критичне напруження прямує до нуля, і навпаки, в міру наближення гнучкості стрижня до нуля критичне напруження прямує до нескінченності.

Однак з умови (4.5) застосованості формули Ейлера відповідно до формули (4.8) маємо

,

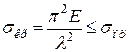і, отже,

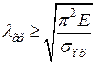. (4.9)

Це означає, що формула Ейлера стає непридатною при гнучкості стрижня, меншій за граничне значення λ_гр, яке залежить тільки від власти­востей матеріалу, тобто в розглядуваному прикладі при

λ < .

Те саме можна дістати і графічно. Якщо на осі ординат (σ_кр) відкласти значення границі пропорційності (σ_пц = 200 МПа) і провести зі здобутої точки К пряму, паралельну осі абсцис, то вона в перетині з гіперболою Ейлера дасть точку М,абсциса якої і є λ_гр. Ліворуч від точки М гіпербо­лу Ейлера зображено штриховою лінією, оскільки вона тут дає значення напружень вищі за границю пропорційності, тобто такі, що не відповіда­ють умовам її застосування.

Проте явище поздовжнього згинання продовжує існувати й за грани­цею пружності. Дослідами встановлено, що дійсні критичні напруження для стрижнів середньої та малої гнучкості λ < λ_гр менші, ніж визначені за формулою Ейлера. Отже, в цьому разі формула Ейлера дає завищені значення критичної сили, тобто завжди переоцінює дійсну стійкість стриж­ня. Тому використання формули Ейлера для стрижнів, що втрачають стійкість за границею пружності, не тільки принципово неправильне, а й дуже небезпечне за своїми наслідками.

Теоретичне розв'язання задачі про стійкість за границею пропорцій­ності складне, тому зазвичай користуються емпіричними формулами, здо­бутими в результаті обробки багатьох дослідних даних.

Ф. С. Ясинський зібрав та обробив великий дослідний матеріал щодо поздовжнього згинання стрижнів, у результаті чого склав таблицю критичних напружень залежно від гнучкості для низки матеріалів та запропонував просту емпіричну формулу для обчислення критичних напружень за границею пропорційності:

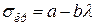. (4.10)

Значення коефіцієнтів а та b для деяких матеріалів наведено в табл. Е.2 (додаток Е). Для чавуну користуються параболічною залежністю

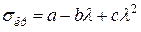, (4.11)

де с = 0,53.

За цими даними для кожного матеріалу при 0 < λ < λ_гр можна побуду­вати графік залежності критичних напружень від гнучкості стрижня.

За деяким значенням гнучкості (позначимо його λ₀) напруження σ_кр, обчислене за формулою (4.10) або (4.11), стає таким, що дорівнює граничному напруженню при стисканні, а саме:

для пластичних матеріалів

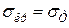
для крихких матеріалів

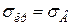. (4.12)

Стрижні, в яких λ < λ₀, називають стрижнями малої гнучкості. Їх розра­ховують тільки на міцність.

У розглядуваному прикладі (рис. 4.4) частина графіка критичних на­пружень за границею пропорційності (при 50 < λ < 100) має вигляд злегка нахиленої прямої SM, а частина (при 0 < λ < 50) – горизонтальної лінії NS. Отже, графік σ_кр = f(λ) для сталі Ст3 складається з трьох частин: гіперболи Ейлера при λ > 100, похилої прямої при 50 < λ < 100 та майже горизонтальної прямої при λ < 50. Похила пряма SM відповідає напруженням між границею пропорційності і границею текучості. Горизонталь­на пряма SN відповідає напруженню, що дорівнює границі текучості.

Читайте також:

1. II. Поняття соціального процесу.
2. V. Поняття та ознаки (характеристики) злочинності
3. А/. Поняття про судовий процес.
4. Абсолютні показники фінансової стійкості
5. Абсолютні показники фінансової стійкості та її типи
6. Адміністративний проступок: поняття, ознаки, види.
7. Адміністративні провадження: поняття, класифікація, стадії
8. Акти застосування юридичних норм: поняття, ознаки, види.
9. Алгебраїчні критерії стійкості
10. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
11. Аналіз фінансової стійкості підприємства
12. АНАЛІЗ ФІНАНСОВОЇ СТІЙКОСТІ ПІДПРИЄМСТВА

Переглядів: 815