• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Циркуляція вектора напруженості магнітного поля. Вихровий характер магнітного поля. Поле довгого соленоїда

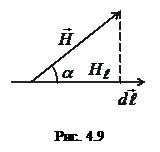Циркуляцією вектора 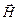по замкненому контуру називається інтеграл де - вектор елементу довжини контура, напрямлений вздовж обходу контура, 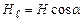– проекція 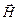на дотичну до контура, α – кут між 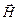та (рис. 4.9).

Розглянемо найпростіший випадок – магнітне поле нескінченно довгого прямолінійного струму. Лініями напруженості цього поля є кола, центри яких лежать на осі провідника, а площини перпендикулярні до нього.

Знайдемо циркуляцію 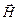вздовж кола радіусом R:

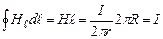, (4.15)

бо .

В загальному випадку, коли провідник охоплений замкненою лінією довільної форми (рис. 4.10, а),

,

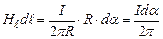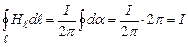. (4.16)

Якщо контур не охоплює провідник зі струмом (рис. 4.10, б), то в (4.16) адже радіальна пряма спочатку рухається в одному напрямку (ділянка 1-2, 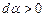), а потім – в іншому (ділянка 2-1, ). Отже,

. (4.17)

Якщо магнітне поле створюється кількома струмами 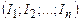, то за принципом суперпозиції і, враховуючи (4.16), остаточно одержимо

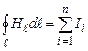. (4.18)

Ця формула є математичним виразом теореми про циркуляцію вектора напруженості магнітного поля: циркуляція вектора напруженості магнітного поля дорівнює алгебраїчній сумі сил струмів, охоплених даним контуром (позитивним вважається струм, що зв’язаний з напрямком обходу правилом свердлика; струм протилежного напрямку вважається негативним). Вираз (4.18) є математичною ознакою вихрового характеру магнітного поля.

Використаємо теорему про циркуляцію 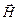для розрахунку магнітного поля довгого соленоїда – циліндричної котушки, на яку намотано N витків дроту. Виберемо контур інтегрування у вигляді прямокутника ABCD, в якому сторона AD лежить всередині соленоїда і паралельна до його осі, а сторона ВС дуже віддалена від соленоїда (рис. 4.11).

Тоді згідно з (4.18)

. (4.19)

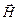Магнітне поле соленоїда швидко зменшується при віддалені від нього, тому . Крім того, оскільки проекціяна сторони AB і CD дорівнює нулю.

Отже, в лівій частині (4.19) залишається один доданок

.

Проекція 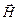на паралельний йому відрізок DA дорівнює модулю цього вектор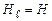а: , а (довжина сторони DA).

Таким чином,

і , (4.20)

де 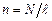– кількість витків на одиниці довжини соленоїда (густина витків). Отже, напруженість магнітного поля всередині довгого соленоїда дорівнює добутку сили струму на густину витків, а індукція поля

. (4.21)

§4.4. Дія магнітного поля на струм; сила Ампера. Магнітна взаємодія струмів

Як відмічалося вище, магнітне поле діє на вміщений у нього провідник зі струмом. Французький фізик Ампер встановив, що на елемент провідника зі струмом , вміщений в магнітне поле індукцією 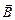, діє сила (сила Ампера)

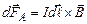(4.22)

або в скалярній формі

, (4.23)

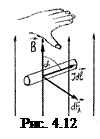
де α – кут між напрямками струму та магнітної індукції. Напрямок сили Ампера можна визначити за правилом лівої руки (рис. 4.12).

Сила, що діє на провідник зі струмом скінченої довжини, знаходиться з (4.22) або (4.23) інтегруванням по всій довжині провідника:

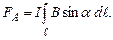(4.24)

Зокрема, для прямолінійного провідника довжиною в однорідному магнітному полі

. (4.25)

Розглянемо тепер взаємодію двох довгих прямолінійних провідників, паралельних один одному і по яких протікають струми однакового напрямку. Ділянки таких провідників зображені на рис. 4.13.

Сила, з якою магнітне поле першого струму діє на ділянку другого провідника довжиною 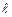, згідно з (4.25)

.

Згідно з (4.13)

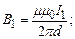
(d – відстань між провідниками).

Як видно з рис. 4.13, кут α між напрямком струму в другому провіднику і вектором магнітної індукції поля першого провідника – прямий; отже, .

Тоді одержимо

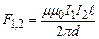. (4.26)

Це і є вираз для сили взаємодії провідників зі струмом (адже так само можна отримати і вираз для сили ). Напрямки сил знайдені за правилом лівої руки і вказані на рис. 4.13. Отже, струми однакового напрямку притягуються. Аналогічно, можна показати, що антипаралельні струми будуть відштовхуватись.

Із формули (4.26), вважаючи в ній всі величини одиничними (за винятком ), отримаємо визначення одиниці сили струму: ампер – це сила такого постійного струму, який при проходженні по двох прямолінійних паралельних нескінченно довгих провідниках, розміщених на відстані 1м у вакуумі, викликає між ними магнітну взаємодію силою 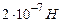на кожен метр довжини. Це визначення використовувалось в СІ до 90-их років минулого століття.

Читайте також:

1. I. Загальна характеристика політичної та правової думки античної Греції.
2. II. ВИРОБНИЧА ХАРАКТЕРИСТИКА ПРОФЕСІЇ
3. II. Морфофункціональна характеристика відділів головного мозку
4. V. Поняття та ознаки (характеристики) злочинності
5. VII. Нахождение общего решения методом характеристик
6. Аварії на хімічно-небезпечних об’єктах та характеристика зон хімічного зараження.
7. Автобіографія. Резюме. Характеристика. Рекомендаційний лист
8. Автокореляційна характеристика системи
9. Активний бюджетний дефіцитхарактеризу­ється спрямуванням коштів на інвестування еко­номіки, що сприяє зростанню ВВП.
10. Активний характер соціальної політики.
11. Акустичні характеристики порід
12. Акцентуації характеру

Переглядів: 2257