• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

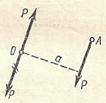
Приведення сили до даного центру.

Нехай дана сила Р, що прикладена в якій-небудь точці А (рис. 3). Візьмемо довільну точку О та додамо до неї дві сили, рівні Р, їй паралельні й спрямовані в протилежні сторони.

Подібне перетворення можна розглядати як результат заміни даної сили Р іншою, паралельною їй силою Р, прикладеною в довільній точці О (на рис. 3 ця сила відзначена двома рисками), і парою (Р, Р) із плечем а, момент якої: М = + Ра.

Рис. 3.

Знак плюс у цій формулі відповідає прийнятому правилу знаків для моменту пари сил.

Заміну даної сили Р, прикладеної в точці А, силою Р, прикладеною в крапці О, і парою (Р, Р) будемо називати приведенням даної сили Р к точці О. Крапка О називається центром приведення, а пара (Р, Р) - приєднаною парою.

Не важко помітити, що момент приєднаної пари дорівнює моменту даної сили Р відносно центра приведення О.

3. Приведення довільної системи сил до даного центру.

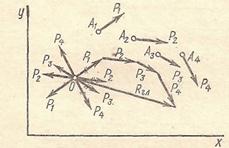
Дано систему сил (наприклад, чотири сили Р₁, Р₂, Р₃, Р₄), розташованих як завгодно на площині (рис. 1). Потрібно скласти ці сили.

Візьмемо довільну точку О і приведемо всі дані сили до цієї точки, скористуючись способом приведення сили до точки.

Рис. 1.

В результаті приведення отримаємо сили Р₁, Р₂, Р₃ і Р₄, що прикладені у точці О (позначені на рисунку двома рисками), і приєднані пари (Р₁, Р₁), (Р₂, Р₂) (Р₃, Р₃) і (Р₄, Р₄), моменти яких дорівнюють моментам даних сил відносно точки О. Тобто, позначаючи моменти пар відповідно М₁, М₂, М₃ і М₄, а моменти сил М_О(Р₁), М_О(Р2), М_О(Р₃) і М_О(Р₄), отримаємо:

М₁ = М_О(Р₁), М₂ = М_О(Р₂), М₃ = М_О(Р₃), М₄ = М_О(Р₄) (1)

Складаючи сили Р₁, Р₂, Р₃ і Р₄, прикладені в центрі приведення 0 (відзначені на рисунку двома рисками): одержуємо результуючу силу R_гл, що дорівнює їх геометричній сумі й прикладену в тій же точці О:

R_гл= Р₁ + Р₂ + Р₃ + Р₄.

Складаючи пари (Р₁, Р₁), (Р₂, Р₂) (Р₃, Р₃) і (Р₄, Р₄) - одержимо результуючу пару, момент якої М_гл дорівнює алгебраїчній сумі моментів пар, що його складають. Отже:

М_гл=М₁ + М₂ + М₃ +М₄. (2)

Маючи на увазі рівності (1), вираження (2) можна надати так:

М_гл = М₀(Р₁) + М₀(Р₂) + М₀(Р₃) + М₀(Р₄), або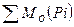

4. Головний вектор і головний момент.

Геометрична сума даних сил R_гл називається головним вектором, алгебраїчна сума моментів цих сил відносно центра приведення М_гл – головним моментом.

Система сил, розташованих як завгодно на площині, завжди може бути приведена до сили, що дорівнює їх головному вектору та доданій в будь-якій точці О, та до пари, момент якої дорівнює головному моменту даних сил відносно тієї ж точки.

5. Рівновага плоскої довільної системи сил.

Плоска довільна система сил знаходиться в стані рівноваги тільки коли:

;

Випадки приведення ПСС:

1. , - система пар сил, приводиться до пари сил (викликає обертаючу дію);

2. , - плоска система збіжних сил, приводиться до рівнодіючої (викликає поступовий рух);

, - врівноважена плоска система сил

6. Рівняння рівноваги плоскої довільної системи сил.

Рівняння: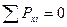

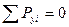
виражають аналітичні умови рівноваги плоскої довільної системи сил.

Таким чином, для того, аби тверде тіло знаходилось в стані рівноваги, необхідно та достатньо, щоб:

1) сума проекцій всіх сил на вісь х дорівнювала нулю;

2) сума проекцій всіх сил на вісь у дорівнювала нулю;

3) сума моментів всіх сил відносно будь-якої точки площини дорівнювала нулю.

7. Класифікація балок, види опорів балок та їх реакції.

Класифікація балок :

1. Балка консольна

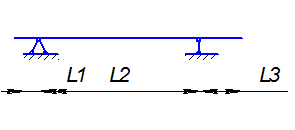
2. Балка шарнірна

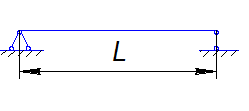
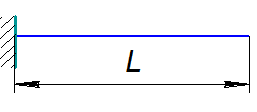
3. Балка – консоль

Види опор балок:

1. Шарнірно-нерухома

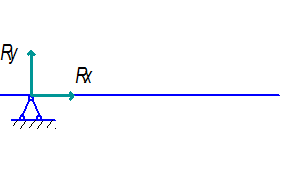
2. Шарнірно-рухома

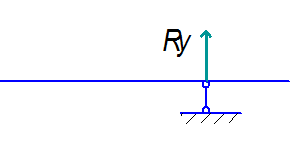
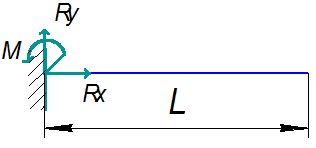
3. Жорстке кріплення

Читайте також:

1. Види приведення даних
2. Відбиває взаємозв'язок їх внутрішніх функціональних підрозділів і модифікується залежно від загальної кількості стратегій даного суб'єкта.
3. Відшкодування збитку, завданого з вини працівника
4. Держава- політична організація даного суспільства (країни) з певним режимом влади і органами управління.
5. Для одиничного і дрібносерійного виробництва норма витрати визначається як укрупнена, наприклад, на 1000 станко-годин роботи даного виду роботи устаткування
6. За даного розподілу владних повноважень районні державні адміністрацій будуть ліквідовані.
7. Перехід від додатного числа, заданого в мінус-двійковій системі числення до від’ємного і навпаки
8. Правовий механізм даного податку закріплено у розділі 13 ПКУ.
9. При виробленні найкращих механізмів подолання дитячої безпритульності доцільно звернутись до міжнародного досвіду та до досвіду інших країн у вирішенні даного питання.
10. Приведення булевих функцій до досконалих диз’юнктивних і кон’юнктивних нормальних форм
11. Приведення національної шкали оцінювання до системи ЕСТS
12. Приведення організаційної структури у відповідність до стратегії.

Переглядів: 2221