• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язок плоскої задачі в напруженнях. Функція напружень. Бігармонічне рівняння плоскої задачі теорії пружності.

Розв’язок плоскої задачі теорії пружності методом тригонометричних рядів Рибьєра-Фурьє.

Розв’язок плоскої задачі теорії пружності в поліномах.

Розв’язок плоскої задачі в напруженнях. Функція напружень. Бігармонічне рівняння плоскої задачі теорії пружності.

Тема: Методи розв’язку плоскої задачі теорії пружності.

Розв’язок плоскої задачі в напруженнях зводиться до розрахунку трьох невідомих функцій σ_x(x, y), σ_y(x, y), τ_xy(x, y). Для цього використовують, вже відомі, два диференціальних рівняння рівноваги (4.14),

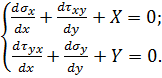
до яких потрібно додати рівняння неперервності деформацій (4.17),

замінивши в останньому деформації на напруження за допомогою формул закону Гука (4.20) для узагальненого плоского напруженого стану

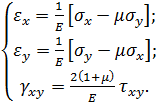
Після сумісного розгляду рівнянь (4.17) та (4.20), виконавши ряд перетворень отримаємо:

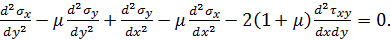
Виключимо з останнього рівняння τ_xy. Для цього перше рівняння рівноваги (4.14) продиференцюємо по х, а друге – по у (вважаємо об’ємні сили – сталою величиною), та складемо їх почленно. Після цього отримаємо:

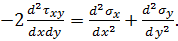
Підставимо отримане співвідношення в попереднє рівняння:

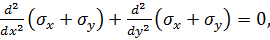
або в скороченому вигляді

(5.1)

Останнє рівняння носить назву рівняння Леві для узагальненого плоского напруженого стану.

Таким чином, сума нормальних напружень в плоскій задачі є гармонічною функцією.

Отже, розв’язок плоскої задачі теорії пружності за умови сталої величини об’ємних сил зводиться до інтегрування трьох рівнянь: двох рівнянь рівноваги (4.14) та рівняння неперервності деформацій (5.1):

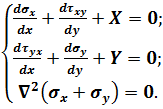(5.2)

При цьому обов’язково повинні виконуватися умови на поверхні (4.15)

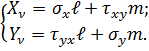
Функція напружень. Бігармонічне рівняння плоскої задачі теорії пружності. Розв’язок плоскої задачі в напруженнях за допомогою рівнянь (5.2) можна істотно спростити, якщо перейти від трьох невідомих функцій σ_x(x, y), σ_y(x, y), τ_xy(x, y) до однієї функції φ = φ(х, у), яка носить назву функції напружень Ері. ЇЇ обирають таким чином, щоб диференціальні рівняння рівноваги (4.14) оберталися в тотожності. Ця умова буде задовольнятися, якщо напруження виразити через функцію Ері за допомогою наступних співвідношень:

(5.3)

Дійсно, якщо підставити ці вирази в рівняння рівноваги (4.14), отримаємо тотожності, тобто прийнята функція напружень φ (х, у) є розв’язком цих рівнянь.

Підставивши напруження з (5.3) в рівняння неперервності деформацій (5.1), отримаємо:

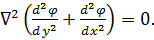
Вираз, який знаходиться в дужках, представляє собою оператор Лапласа над функцією φ (х, у). В зв’язку з цим останнє рівняння може бути представлено за допомогою оператора Лапласа, а саме:

(5.4)

Ліва частина останнього виразу називається подвійним оператором Лапласа над функцією φ.

Записавши рівняння (5.4) в розгорнутому вигляді та виконавши його диференціювання, отримаємо:

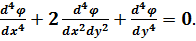(5.5)

Як рівняння (5.4), так і рівняння (5.5) носить назву – бігармонічне рівня плоскої задачі. Воно представляє собою умову сумісності деформацій, виражену через функцію напружень φ.

Виразимо умови на поверхні для плоскої задачі (4.15) через функцію напружень за допомогою рівнянь (5.3):

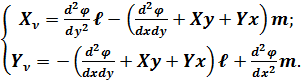(5.6)

Отже, плоска задача теорії пружності зведена до визначення однієї бігармонічної функції φ (х, у), що задовольняє заданим умовам на контурі.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. А .Маршалл - основоположник неокласичної теорії.
3. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
4. Алгоритм розв’язання задачі
5. Алгоритм розв’язання розподільної задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі
11. Алгоритм розв’язування задачі
12. Алгоритм розв’язування задачі оптимізації в Excel

Переглядів: 1589