Одноканальні системи масового обслуговування

Розглянемо одноканальну СМО з одним пристроєм для обслуговування S і чергою до нього q, яку зображено на рис. 2.7.

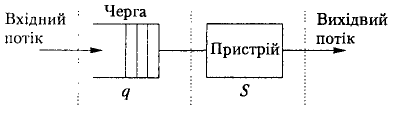
Рис. 2.7. СМО з одним пристроєм для обслуговування

Якщо позначити через w середній час перебування вимоги в черзі, то з формули Литтла можна отримати середню кількість вимог у черзі:

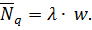
Якщо позначити середній час обслуговування вимоги в пристрої через і розглядати СМО як таку, що має один пристрій, то, використовуючи формулу Литтла, можна знайти середню кількість вимог у пристрої для обслуговування:

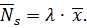
Для СМО з одним пристроєм для обслуговування завжди має місце рівність

де Т — середній час перебування вимоги в системі.

Коефіцієнт завантаження (коефіцієнт використання) пристрою для обслуговування r можна визначити, якщо розділити інтенсивність надходження вимог до системи (l) на швидкість обслуговування цих вимог у пристрої (m), тобто

де

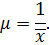
Тоді

Покажемо, що r — це ймовірність того, що під час надходження вимоги до системи пристрій для обслуговування буде зайнятим. Розглянемо як задовгий проміжок часу t. Відповідно до закону великих чисел, очікувана кількість вимог на проміжку часу t з імовірністю 1 буде приблизно дорівнювати lt. Позначимо через р₀ імовірність того, що в деякий випадковий момент часу вимога, що надійшла, застане пристрій вільним. Тоді можна стверджувати, що на проміжку часу t пристрій буде зайнятим t(1–р₀). Таким чином, з імовірністю 1 кількість обслужених за цей проміжок часу вимог буде дуже близькою до величини

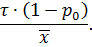
Якщо всі вимоги, які надійшли за проміжок часу t, вважати обслуженими, то

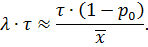
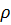Таким чином, маємо , якщо , або , тобто з імовірністю вимога застає пристрій для обслуговування зайнятим, або 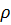дорівнює частці часу, протягом якого пристрій був зайнятим.

Введемо коефіцієнт варіації С як відношення стандартного відхилення від середнього значення до середнього значення :

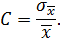
Для експоненціального закону розподілу коефіцієнт варіації С = 1, оскільки і для цього закону дорівнюють l. Для регулярного детермінованого закону розподілу С = 0 (). Таким чином, для моделі СМО типу G/G/1 з одним пристроєм і при довільних законах надходження та обслуговування вимог середня кількість вимог визначається як

Цей вираз можна отримати [21], якщо відзначити, що кількість вимог, які залишилися в системі після виходу деякої вимоги, є напівмарківським процесом з укладеним ланцюгом Маркова, який визначено в моменти виходу вимоги.

Використовуючи результат Хінчина-Полячека, можна отримати середній час перебування вимог у одноканальній СМО за формулою

(2.6)

Із формули (2.6) видно, що середній час перебування вимоги в системі залежить тільки від математичного сподівання і стандартного відхилення часу обслуговування. Таким чином, час чекання визначається як

Зазвичай потрібно знати нормований час чекання:

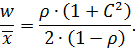
Для моделей типу М/М/1

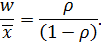
Для моделей типу M/D/1

Таким чином, система з регулярним законом обслуговування характеризується середнім часом чекання, удвоє меншим, ніж для системи з показовим законом обслуговування. Це закономірно, оскільки час перебування вимог у системі та їх кількість пропорційні дисперсії часу обслуговування.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Вихідний потік вимог	\|	Багатоканальні системи масового обслуговування

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.016 сек.