
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Дві основні задачі динаміки
Перша, або пряма основна задача динаміки: знаючи закон руху точки і її масу, визначити сили, що викликають цей рух.
Якщо рух матеріальної точки масою m задано координатним способом 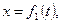
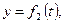
 , то двічі диференціюючи ці співвідношення за часом, одержимо проекції прискорень на координатні осі:
, то двічі диференціюючи ці співвідношення за часом, одержимо проекції прискорень на координатні осі:
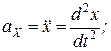

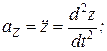 .
.
Використовуючи динамічні рівняння руху матеріальної точки в координатній формі , визначимо проекції сили:
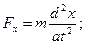
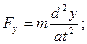
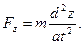
Модуль рівнодійної сили 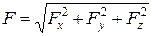 .
.
Напрям рівнодійної сили визначимо за направленими косинусами

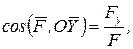
 .
.
Методами першої основної задачі динаміки вирішують такі задачі транспортників , як тиск вагона на рейки.
Приклад 1. Кузов трамвайного вагона разом з вантажем P1=100 кH здійснює при русі на ресорах вертикальні коливання по закону 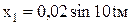 на візку з колесами (рис. 8.1). Визначити найбільший і найменший тиск вагона на рейки 3 горизонтального прямолінійного відрізку шляху , якщо візок з колесами важить Р2 =10кН.
на візку з колесами (рис. 8.1). Визначити найбільший і найменший тиск вагона на рейки 3 горизонтального прямолінійного відрізку шляху , якщо візок з колесами важить Р2 =10кН.
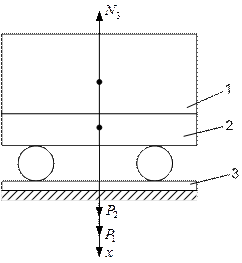 Рис. 8.1
Рис. 8.1
| Розв’язання
Розглянемо рух кузова. Рух цей прямолінійний і проходить уздовж осі х. Тому з трьох рівнянь руху використаємо одне, що в даному випадку приймає вигляд
 де
де 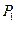 и и  ‑ відомі з умов приклада ваги кузова і візка з колесами, ‑ відомі з умов приклада ваги кузова і візка з колесами,
|
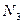 ‑ реактивна сила з боку в’язів, рейки.
‑ реактивна сила з боку в’язів, рейки.
Звідси  .
.
З умови приклада маємо :
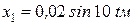 ‑ закон руху кузова на ресорах.
‑ закон руху кузова на ресорах.
Тоді  ,
,
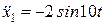 ‑ проекція прискорення кузова в напрямку осі х
‑ проекція прискорення кузова в напрямку осі х
 ;
;
 .
.
Звідси  ;
;
 .
.
Відповідь: 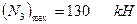 .
.

Друга, або обернена задача динаміки: визначити кінематичні рівняння руху точки, якщо відомі її маса m, прикладені до неї сили  і початкові умови руху. Розв’язання другої задачі динаміки зводиться до інтегрування диференційних рівнянь руху матеріальної точки. Праві частини цих рівнянь відомі. Тому спочатку знаходять проекції сил иF на осі координат (Fx,FyFz), потім інтегрують системи диференційних рівнянь руху матеріальної точки.
і початкові умови руху. Розв’язання другої задачі динаміки зводиться до інтегрування диференційних рівнянь руху матеріальної точки. Праві частини цих рівнянь відомі. Тому спочатку знаходять проекції сил иF на осі координат (Fx,FyFz), потім інтегрують системи диференційних рівнянь руху матеріальної точки.
Загальний розв¢язок цієї системи визначає координати точки як функції часу t і шість сталих інтегрування 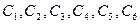 ;
;
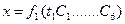 ,
,
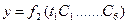 ,
,
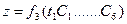 .
.
Сталі інтегрування визначають з початкових умов.
Початкові умови – це шість величин, що визначають положення точки і проекції вектора швидкості в початковий момент часу (t=t );
);
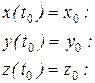
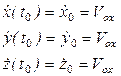
Підставивши знайдені значення сталих інтегрування у загальній розв'язок системи диференційних рівнянь, одержують закон руху точки:
x = x(t); y = y(t); z = z(t).
Отже, розв’язання другої, оберненої задачі динаміки складається з операцій:
1. Складання динамічних рівнянь руху матеріальної точки згідно з умовами задачі.
2. Інтегрування одержаної системи диференційних рівнянь.
3. Визначення значень сталих інтегрування.
4. Знаходження закону руху.
Приклад 2. Маємо рух матеріальної точки, кинутої під кутом до обрію.
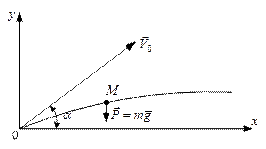 Рис. 8.2
Рис. 8.2
| Визначити рух точки М масою m, яку кинуто з початковою швидкістю V під кутом під кутом  до обрію. Опором повітря знехтувати (рис. 8.2). Визначити траєкторію руху точки. до обрію. Опором повітря знехтувати (рис. 8.2). Визначити траєкторію руху точки.
|
Розв’язання. Початок координат показуємо в початковому положенні точки. Зобразимо рухому матеріальну точку M в довільній точці траєкторії і покажемо діючу на неї силу тяжіння 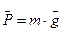 .
.
У початковий момент часу (t = 0) точка була на початку координат, тому при t=0, x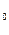 =0; y
=0; y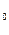 =0.
=0.
Проекції початкової швидкості на осі координат:
при 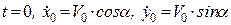 .
.
Щоб визначити залежність координат х, у точки від часу, скористаємося диференційним рівняннями руху точки:
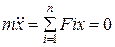 ,
,
 , або після скорочення на m
, або після скорочення на m
 ,
,
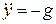 .
.
Інтегруючі ці рівняння, одержимо
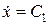 ,
,
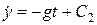 .
.
Сталі інтегрування знайдемо з початкових умов:
при t=0
 ,
,
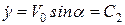 .
.
Отже
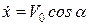 ,
,
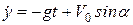 .
.
Звідси після інтегрування одержимо
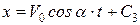 ,
,
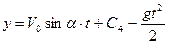 .
.
Сталі інтегрування С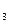 і С
і С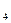 знаходимо з початкових умов руху. При t=0 x
знаходимо з початкових умов руху. При t=0 x =0; y
=0; y =0, тому С
=0, тому С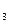 =С
=С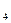 =0
=0
Тоді закон руху точки М матиме вигляд
 ,
,
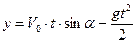 .
.
Ці вирази є рівняннями траєкторії в параметричному вигляді. Вилучивши час з цих рівнянь, знайдемо траєкторію руху точки М:
 .
.
Отримана траєкторія – парабола, яка належить площині ХОУ.
Методику розв’язання другої основної задачі динаміки застосовують при вирішенні задач про прямолінійні коливання матеріальної точки. Аксіома про звільнення від в’язів дає змогу задачу про рух невільної матеріальної точки вважати рухом вільної матеріальної точки, якщо дію в’язів замінити відповідними силами – реакціями в’язів.
Читайте також:
- II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
- Адвокатура в Україні: основні завдання і функції
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі оптимізації в Excel
- Амортизація основних засобів, основні методи амортизації
| <== попередня сторінка | | | наступна сторінка ==> |
| Диференціальні рівняння руху вільної матеріальної точки | | | Прямолінійні коливання матеріальної точки |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |