
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Прямолінійні коливання матеріальної точки
Механічні рухи, які періодично повторюються, називаються механічними коливаннями. На матеріальну точку можуть діяти поновлююча сила, яка намагається повернути точку в положення рівноваги, сила опору руху, яка залежить від швидкості точки, і збурююча сила, задана функцією часу.
Залежно від комбінації цих сил розглянемо три види коливального руху матеріальної точки : вільні коливання під дією тільки лінійної поновлюючої сили, згасаючі коливання під дією поновлюючої сили й сили опору, що залежить від швидкості, й вимушені коливання під дією поновлюючої сили і збурюючої сили, яка змінюється за гармонійним законом.
Вільні (власні коливання)
Вільними (власними) коливаннями матеріальної точки називають її коливання під дією сил, зумовлених початковими умовами: відхилення точки від положення рівноваги або надання їй початкових швидкостей.
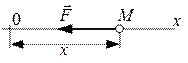 Рис. 8.3
Рис. 8.3
| Розглянемо прямолінійний рух матеріальної точки М масою m під дією тільки сили  , спрямованої до нерухомого центра О і пропорційної відстані точки М від центра О: , спрямованої до нерухомого центра О і пропорційної відстані точки М від центра О: 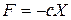 (лінійна залежність) (рис. 8.3). (лінійна залежність) (рис. 8.3).
|
Сила  намагається повернути точку М у положення рівноваги О, де
намагається повернути точку М у положення рівноваги О, де 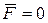 , тому сила
, тому сила  називається поновлюючою силою. Прикладом такої сили є сила пружності пружини.
називається поновлюючою силою. Прикладом такої сили є сила пружності пружини.
Визначити закон руху точки М, тобто закон зміни координати х за часом.
Запишемо диференційне рівняння руху точки за часом у проекції на вісь х:
 ;
; 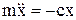 , або
, або 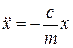 ,
,
 ;
;  ,
,
де 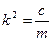 ,
, 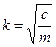 ‑ колова (власна) частота коливань матеріальної точки масою m, вимірюється в рад/с; с – коефіцієнт жорсткості (пружності) пружини, що чисельно дорівнює силі, яку необхідно докласти до пружини, щоб змінити її довжину на одиницю (вимірюється в н/м).
‑ колова (власна) частота коливань матеріальної точки масою m, вимірюється в рад/с; с – коефіцієнт жорсткості (пружності) пружини, що чисельно дорівнює силі, яку необхідно докласти до пружини, щоб змінити її довжину на одиницю (вимірюється в н/м).
Закон коливань точки М має вигляд (рішення диференційного рівняння коливань):
 ,
,  ,
,
де А і В – постійні інтегрування, що визначаються з початкових умов.
Початкові умови: при t=0; x=x ;
; 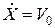 .
.
Враховуючі початкові умови, маємо: 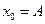 ;
; 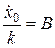 .
.
Остаточно закон коливань точки М має вигляд
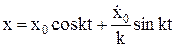 .
.
Якщо замість постійних інтегрування А і В, ввести постійні a і  так, щоб
так, щоб 
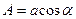 ,
, 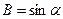 , отримаємо закон коливань у вигляді
, отримаємо закон коливань у вигляді  ,
,
де 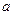 і
і  також визначаються з початкових умов.
також визначаються з початкових умов.
При t=0 


 ,
,  .
.
Тоді  ‑ амплітуда коливань, що дорівнює найбільшому відхиленню точки М від центра D і залежить від початкових умов,
‑ амплітуда коливань, що дорівнює найбільшому відхиленню точки М від центра D і залежить від початкових умов,
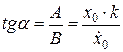 ,
,
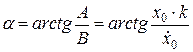 ‑ початкова фаза коливань, яка також залежить від початкових умов.
‑ початкова фаза коливань, яка також залежить від початкових умов.
Розглянутий прямолінійний рух матеріальної точки М масою m під дією сили  , величина якої пропорційна відхиленню точки від положення статичної рівноваги, є гармонійний коливальний рух з власною коловою частотою
, величина якої пропорційна відхиленню точки від положення статичної рівноваги, є гармонійний коливальний рух з власною коловою частотою  періоди
періоди 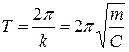 .
.
Період коливань Т – проміжок часу між двома послідовними проходженнями точки через положення статичної рівноваги в певному фіксованому напрямку.
Колова частота власних коливань К і їх період Т не залежать від початкових умов і амплітуди коливань а. Коли одночасно початкові умови дорівнюють нулю  , то х=0, тобто вільні(власні) коливання не виникають.
, то х=0, тобто вільні(власні) коливання не виникають.
Вплив сталої сили на вільні коливання
Розглянемо на прикладі коливання вантажу масою m, підвішеного за допомогою пружини жорсткості С до нерухомої площини, вздовж осі ОХ (рис. 8.4).
На точку М (вантаж вагою Р=mg) діє сила пружності пружини  і сила ваги
і сила ваги  (стала сила).
(стала сила).
Точка О – це початок осі ОХ, спрямованої в бік дії сили 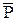 ,
, 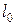 ‑ довжина пружини в недеформованому стані, х – поточна координата вантажу при русі,
‑ довжина пружини в недеформованому стані, х – поточна координата вантажу при русі, 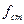 ‑ статична деформація пружини під дією вантажу.
‑ статична деформація пружини під дією вантажу.
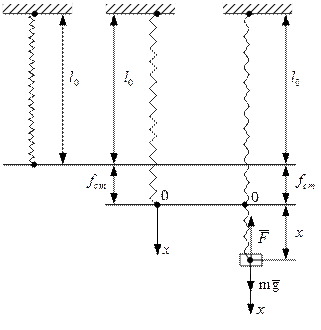
Рис. 8.4
Точка О – це точка статичної рівноваги, де сила Р врівноважена силою пружності пружини 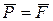
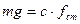 ;
; 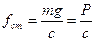 .
.
При русі сила пружності пружини в проекції на вісь ОХ  ,
, 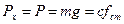 .
.
Диференційне рівняння руху точки М в проекції на вісь ОХ має вигляд
 ,
,
або  ,
,
 .
.
Закон коливання вантажу (рішення диференційного рівняння руху) під дією сталою сили та лінійної поновлюючої сили в цьому випадку має вигляд  , як і у випадку дії тільки поновлюючої сили (рис 8.5).
, як і у випадку дії тільки поновлюючої сили (рис 8.5).
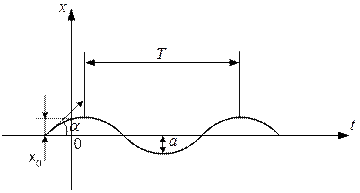 Рис. 8.5
Рис. 8.5
| Стала сила не змінює характеру коливань (за законом синуса або косинуса), зміщуючи центр коливань у бік дії сталої сили вздовж осі ОХ на величину статичної деформації  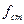 . .
|
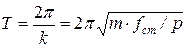 ,
,  ,
,  .
.
Вплив сили опору, що лінійно залежить від швидкості,
на вільні коливання матеріальної точки (загасаючі коливання)
 Рис. 8.6
Рис. 8.6
| Матеріальна точка М (вантаж масою m) рухається під дією сили тяжіння у в’язкому середовищі (рідина або газ), при русі в якій виникає сила опору, пропорційна першому ступеню швидкості.
Таку силу опору називають силою в’язкого тертя:
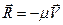 (знак “-“ показує, що сила (знак “-“ показує, що сила 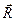 спрямована протилежно спрямована протилежно 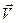 ).
Таким чином, на точку М при русі діють поновлююча сила ).
Таким чином, на точку М при русі діють поновлююча сила  і сила опору і сила опору 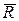 (рис 8.6). (рис 8.6).
|
Диференційне рівняння руху точки (вантажу) має вигляд
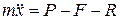 ,
,
або 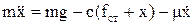 ,
,
або  ,
,
або  ,
,
де  ‑ частота власних коливань (колова);
‑ частота власних коливань (колова);
 ‑ відносний коефіцієнт демпфірування, що має розмірність колової частоти k коливань ([n] = рад/c).
‑ відносний коефіцієнт демпфірування, що має розмірність колової частоти k коливань ([n] = рад/c).
Закон коливання вантажу (рішення диференційного рівняння) залежить від співвідношення параметрів k і n.
1. Закон коливання вантажу у випадку малого опору n<k має вигляд
 ,
,
або  ,
,
де постійні інтегрування визначаються, як і раніше, з початкових умов,
 ‑ частота згасаючих коливань,
‑ частота згасаючих коливань,
 ‑ максимальне відхилення точки від положення рівноваги,
‑ максимальне відхилення точки від положення рівноваги,
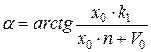 ‑ початкова фаза.
‑ початкова фаза.
Коливання, які відбуваються за цим законом, називаються згасаючими, тому що величина  за перебігом часу, завдяки множнику
за перебігом часу, завдяки множнику  ,зменшується, прямуючи до нуля (рис. 8.7).
,зменшується, прямуючи до нуля (рис. 8.7).
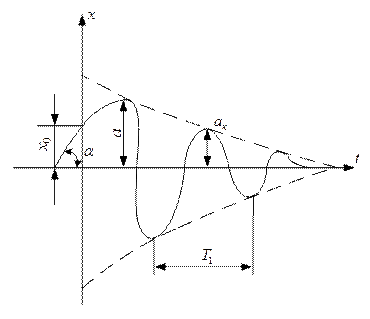
Рис. 8.7
Періодом згасаючих коливань Т1 називають проміжок часу між двома послідовними проходженнями точки через положення статичної рівноваги в певному фіксованому напрямку:
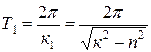 .
.
Звідси видно, що період згасаючих коливань більший за період власних коливань Т1>T. Опір середовища, що пропорційний швидкості в першому ступені, збільшує період коливань.
Співвідношення  називають декрементом загасання, або фактором загасання.
називають декрементом загасання, або фактором загасання.
Амплітуда згасаючих коливань спадає за геометричною прогресією.
2. При 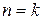 рішення диференційного рівняння руху:
рішення диференційного рівняння руху: 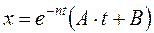 .
.
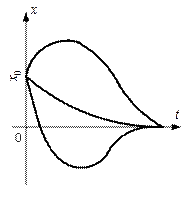 Рис. 8.8
Рис. 8.8
| Рух точки буде аперіодичним згасаючим, не буде коливальним і за перебігом часу буде спрямовуватися до нуля ( при при 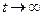 ). Рух точки залежить від початкових умов (рис. 8.8).
3. При n > k, коли опір великий по рівнянно з поновлюючою силою, рішення диференційного рівняння руху має вигляд: ). Рух точки залежить від початкових умов (рис. 8.8).
3. При n > k, коли опір великий по рівнянно з поновлюючою силою, рішення диференційного рівняння руху має вигляд:
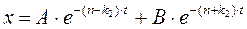 ,
де ,
де  . .
|
Рух точки в цьому випадку також не є коливальним і вона під дією наповнюючої сили поступово (асимптотично) буде спрямовуватися до стану рівноваги х=0. Рух точки також залежить від початкових умов і є аперіодичним (рис 8.9).
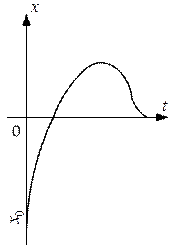
Рис. 8.9
Читайте також:
- АВТОКОЛИВАННЯ
- Алгебраїчний спосіб визначення точки беззбитковості
- Аналіз точки беззбитковості
- Видалення характерної точки
- Види матеріальної відповідальності
- Види матеріальної відповідальності. Обмежена матеріальна відповідальність робітників і службовців
- Визначення точки
- Визначення точки беззбитковості
- Визначення точки беззбитковості.
- Визначення. Точки максимуму й мінімуму функції називаються точками екстремуму.
- Вимушені електромагнітні коливання
- Вимушені коливання
| <== попередня сторінка | | | наступна сторінка ==> |
| Дві основні задачі динаміки | | | Змушені коливання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |