Емпірична функція розподілу, гістограма

Оскільки невідомий розподіл F можна описати, наприклад, його функцією розподілу F, побудуємо по вибірці «наближення» для цієї функції.

Визначення 1.Емпіричною функцією розподілу, побудовану по вибірці X= (Х,... ,Х_п) обсягу п називається випадкова функція F_n^* : R*W ® [0,1], при кожномуyє R рівна

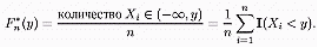
Нагадування:функція

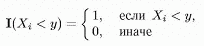
називається індикатором події {X_i < у}. Це — випадкова величина, що має розподіл Бернулі з параметром р = P(Xi < у) = F(y) (чому?).

Якщо елементи вибірки Х₁,..., Х_п упорядкувати по зростанню (на кожному елементарному результаті), вийде новий набір випадкових величин, названий варіаційним рядом:

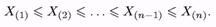
Тут Х₍₁₎ = min{X₁,..., Х_п}, Х(п) = max{X₁,..., Х_п}. Елемент X(k), k = 1,..., п, називається k-м членом варіаційного ряду чи k-ю порядковою статистикою.

Приклад 1.Вибірка, п = 15: X = (0; 2; 1; 2,6; 3,1; 4,6; 1; 4,6; 6; 2,6; 6; 7; 9; 9; 2,6). Варіаційний ряд: (0; 1; 1; 2; 2,6; 2,6; 2,6; 3,1; 4,6; 4,6; 6; 6; 7; 9; 9).

Емпірична функція розподілу має стрибки в точках вибірки, величина стрибка в точці X_i дорівнює т/п, де т — кількість елементів вибірки, що збігаються з X_i.

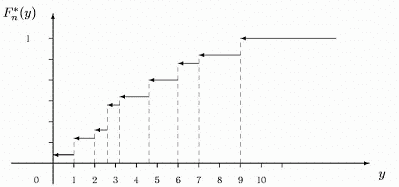
Рис. 1: Приклад 1 Можна зобразити емпіричну функцію розподілу так:

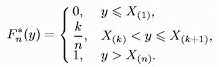
Іншою характеристикою розподілу є таблиця (для дискретних розподілів) чи щільність (для абсолютно неперервних). Емпіричним, чи вибірковим аналогом таблиці або щільності є так звана гістограма.

Гістограма будується по згрупованим даним. Передбачувану область значень випадкової величини ξ (чи область вибіркових даних) поділяють незалежно від вибірки на деяку кількість інтервалів (частіше — однакових, але не обов'язково). Нехай a₁, ..., А_k — інтервали групи. Позначимо для j = 1,..., k через n_j число елементів вибірки, що потрапили в інтервал A_j:

На кожнім з інтервалів a_j будують прямокутник, площа якого пропорційна n_j. Загальна площа всіх прямокутників повинна дорівнювати одиниці. Нехай l_j — довжина інтервалу a_j. Висота прямокутника над a_jдорівнює

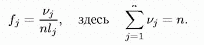
Отримана фігура називається гістограмою.

Приклад 2.Маємо варіаційний ряд (див. 1):

(0; 1; 1; 2; 2,6; 2,6; 2,6; 3,1; 4,6; 4,6; 6; 6; 7; 9; 9).

Розіб'ємо відрізок [0,10] на 4 рівних відрізки. У відрізок А₁ = [0; 2,5) потрапили 4 елементи вибірки, в А₂ = [2,5; 5) — 6, у A₃ = [5; 7,5) — 3, і у відрізок А₄ = [7,5; 10] потрапили 2 елементи вибірки. Будуємо гістограму (ліворуч). Праворуч — теж гістограма для тієї ж вибірки, але при розбивці області на 5 рівних відрізків.

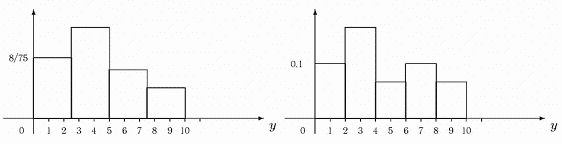
Рис. 2: Приклад 2

Зауваження 1.Як стверджується в курсі «Економетрія», найкращим числом інтервалів групи («формула Стерджесса») є

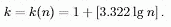
Тут lg п — десятковий логарифм, тому k = 1 + Iog₂ 101og₁₀ n = 1 + log₂ n, тобто при збільшенні вибірки в 2 рази число інтервалів групи збільшується на 1.

Помітимо, що чим більше інтервалів групи, тим краще. Але це «чим більше» має свої границі: якщо брати число інтервалів, скажемо, порядку п, то з ростом п гістограма, мабуть, не буде поточечнонаближатися до щільності.

Справедливо наступне твердження: якщо щільність розподілу елементів вибірки є неперервною функцією, то при k(n) ® µ, так що k(n)/n ® 0, має місце поточечна збіжність по ймовірності гістограми до щільності (див. зауваження 1).

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Основні поняття вибіркового методу	\|	Збіжність емпіричних характеристик до теоретичних

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.