• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Плавне розширення русла - дифузор

Рис. 4.12. Раптове розширення русла

Враховуючи співвідношення швидкостей, одержуємо

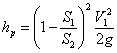
(4.25)

Порівнюючи даний вираз з формулою Вейсбаха, можна зробити висновок, що

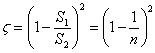
(4.26)

де n = S₂/S₁ - ступінь розширення русла.

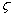У окремому випадку, коли рідина подається по трубопроводу у великий резервуар коефіцієнт опору _Р=1,а h_p = 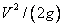, тобто в місцевому опорі втрачається весь швидкісний напор.

Дифузор характеризується кутом розширення 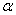і ступенем розширення n = S₂/S₁ (рис. 4.13)

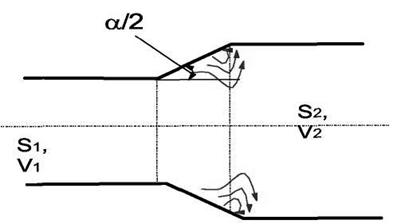
Рис. 4.13. Вихроутворення в дифузорі

При перебігу рідини в дифузорі швидкість плавно зменшується, а тиск плавно зростає. Частинки рідини долають тиск, що підвищується, за рахунок своєї кінетичної енергії. Біля стінок за рахунок малих швидкостей виникає зворотна течія, з'являється відрив потоку, який обумовлює втрати на вихроутворення. Крім того, мають місце втрати на тертя, тобто .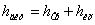

Застосувавши формулу Дарсі для визначення втрат на тертя, враховуючи при цьому геометричні параметри дифузора, а також те, що втрати на вихроутворення за своєю природою аналогічні втратам при раптовому розширенні русла, але менше їх по величині (цей факт враховується коефіцієнтом пом'якшення удару К) можна одержати вираз для втрат напору в дифузорі

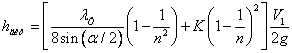
(4.27)

Коефіцієнт К при 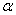=5-20° можна приймати К = sin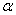. Залежність 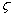_диф = f(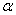) має вигляд, представлений на рис. 4.14

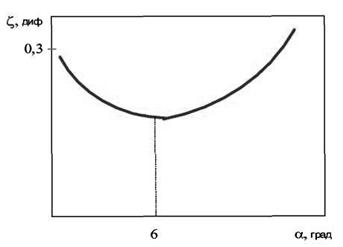
Рис. 4.14. Графік залежності 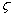_диф= f()

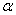Наявність 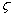_опт пояснюється тим, що при малих 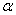переважають втрати на тертя, а при більших – на вихроутворення. Для конічних дифузорів 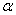_опт = 6...7⁰ (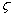_опт 0,15).

Для плоских – 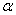_опт = 10.. 12⁰ .

Читайте також:

1. Загальними мотивами, що спонукають фірми брати участь у міжнародному бізнесі, є можливість розширення продажу, придбання нових джерел ресурсів, диверсифікація.
2. Заняття ф.в. у межах розширення активного відпочинку.
3. Здатність до стиску та температурне розширення
4. Зміна висоти голосу, тобто розширення його діапазону
5. Зміною в ціннісній пропозиції товару або послуги може бути абсолютно новий товар або послуга або ж розширення існуючої пропозиції.
6. Князювання Святослава (964—972 рр.) — сина Ольги й Іго­ря — було спрямовано в основному на розширення кордонів Русі і збройну боротьбу із сусідами.
7. Необхідність розширення множини цілих чисел.
8. Обмежувальні розширення сертифіката
9. Плавне звуження русла - конфузор
10. Плавне опускання покрівлі
11. Поворот русла

Переглядів: 630