
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Раптове розширення русла
Вакуум
Таблиця 1
| Рідина | 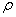 , кг/м3 , кг/м3
|  , МПа-1 , МПа-1
| 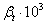 , 0C-1 , 0C-1
|  ×106,м2/с ×106,м2/с
| 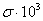 , Н/м , Н/м
|
| Вода | 0,49 | 0,15 | 1,01 | ||
| Спирт етиловий | 0,78 | 1,10 | 1,52 | ||
| Гліцерин | 0,22 | 0,50 | |||
| Бензин | 680-780 | 0,77 | 1,26 | 0,65 | |
| Ртуть | 0,04 | 0,18 | 0,11 | ||
| Масло індустр. 50 | 0,68 | 0,7 | |||
| АМГ-10 | 0,76 | 0,83 |
Пристрої для вивчення і визначення фізичних властивостей рідин
Термометрслужить для визначення теплового розширення рідини, що міститься в ньому. Термометр має скляний балон з капіляром, заповненим термометричною рідиною, і шкалу. Принцип його дії заснований на тепловому розширенні рідин.
Варіювання температури навколишнього середовища приводить до відповідної зміни об'єму термометричної рідини і, отже, її рівня в капілярі. Рівень указує на шкалі значення температури.
Ареометрслужить для вимірювання щільності водного розчину гліцерину або спирту поплавковим методом і є порожнистим циліндром із стержнем у верхній частині. Нижня частина циліндра заповнена дробом для забезпечення вертикального положення ареометра в досліджуваній рідині. Глибина занурення ареометра є функцією щільності, що прочитується зі шкали на стержні по верхньому краю меніска рідини навколо стержня.
ВіскозиметрСтокса дозволяє визначити в'язкість рідини за швидкістю падіння в ній кульки. Прилад містить циліндричну порожнину з центруючими каналами на кінцях і кулькою. Центруючі канали забезпечують падіння кульки по осі порожнини. Порожнина приладу заповнена водно-гліцериновим розчином.
ВіскозиметрОствальда включає невелику ємність з капіляром. В'язкість визначається за часом витікання рідини з її місткості через капіляр.
Сталагмометр служить для визначення поверхневого натягу рідини методом відриву крапель. Сила поверхневого натягу у момент відриву крапель рівна їх вазі, яка легко обчислюється по густині рідини і числу крапель, одержаному при спорожненні місткості сталагмометра заданого об'єму.
Тема 2. ЗАКОНИ РІДИНИ (ГІДРОСТАТИКА)
2.1. Гідростатичний тиск і його властивості.
2.2. Диференціальне рівняння рівноваги рідини.
2.3. Основне рівняння гідростатики.
2.4. Прикладні питання гідростатики.
2.1. Гідростатичний тиск і його властивості
У рідині, що перебуває у стані спокою, можливий лише один вид напруження - напруження стиснення, тобто гідростатичний тиск.
Існує дві основні властивості гідростатичного тиску в рідині:
1. На зовнішній поверхні рідини гідростатичний тиск завжди направлений по нормалі всередину даного об'єму рідини. Ця властивість витікає з визначення тиску, як напруження нормально стискаючої сили.
2. У будь-якій точці усередині рідини гідростатичний тиск у всіх напрямках однаковий, тобто тиск не залежить від кута нахилу площадки, на яку він діє в даній точці.
Доведемо цю властивість. Виділимо в нерухомій рідині елементарний об'єм у формі прямокутного тетраедра з ребрами, паралельними координатним осям і відповідно рівними dx, dy і dz (див. рис.2.1).
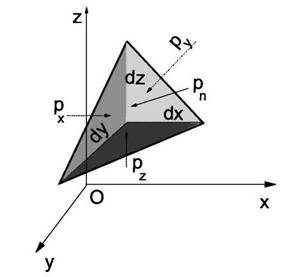
Рис. 2.1. До розгляду властивостей гідростатичного тиску
Хай поблизу виділеного об'єму на рідині діє одинична масова сила, складові якої рівні Х, Y і Z.
Позначимо через рх гідростатичний тиск, що діє на грань, нормальну до осі ОХ, через ру - тиск на грань, нормальну до осі ОУ і т.д. Гідростатичний тиск, що діє на грань похилої, позначимо через рn,, а площа цієї грані dS. Всі ці тиски направлені по нормалях до відповідних площадок.
Складемо рівняння рівноваги виділеного об'єму рідини уздовж осі ОХ, тоді сила тиску уздовж осі 0Х рівна
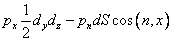 .
.
Маса тетраедра рівна добутку його об'єму на густину, тобто 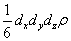 . Отже, масова сила, що діє на тетраедр уздовж осі ОХ, рівна
. Отже, масова сила, що діє на тетраедр уздовж осі ОХ, рівна
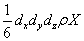 .
.
Тоді, рівняння рівноваги тетраедра запишеться в наступному вигляді:
 .
.
Розділимо це рівняння почленно на площу 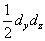 ,яка є проекцією грані похилої dS на площину yОz, і, отже
,яка є проекцією грані похилої dS на площину yОz, і, отже
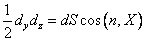 .
.
Матимемо 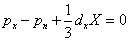 .
.
При прагненні розмірів тетраедра до нуля останній член рівняння, що містить множник dx, також прагнутиме до нуля, а тиск рх і рn залишатимуться кінцевими величинами. Отже, в межі px - pn = 0, рх = рn.
Аналогічну рівність одержимо для тиску ру і рz уздовж відповідних осей Оy і Оz після таких же міркувань: ру = рn, рz = рn,
А, отже
| ру = рn, рz = рn, | (2.1) |
що і потрібно було довести.
Оскільки розміри тетраедра dx, dy і dz були узяті довільно, то нахил площадки dS довільний. При стяганні тетраедра в точку тиски в цій точці по всіх напрямах будуть однакові.
Доведена властивість гідростатичного тиску в нерухомій рідині має місце також при русі нев'язкої рідини. При русі ж в'язкої рідини виникає дотичне напруження, унаслідок чого гідромеханічний тиск у в'язкій рідині вказаною властивістю не володіє.
2.2. Основне рівняння гідростатики
Розглянемо основний випадок рівноваги однорідної рідини, коли з масових сил на рідину діє лише сила тяжіння (відсутня сила інерції рухомої рідини).
Хай рідина міститься в судині (рис.2.2) і на її вільну поверхню діє тиск ро.
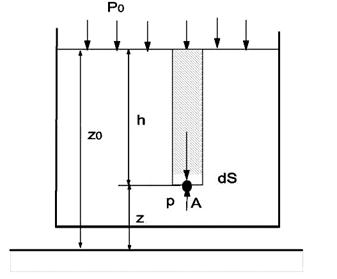
Рис. 2.2. До висновку основного рівняння гідростатики
Знайдемо величину гідростатичного тиску р в довільно узятій точці А, розташованій на відстані h від вільної поверхні. Для цього візьмемо елементарну горизонтальну площадку dS, центром якої є точка А, і побудуємо на цій площадці вертикальний циліндр висотою h. Розглянемо умову рівноваги цього об'єму рідини, для чого запишемо суму всіх сил, що діють на даний об'єм по вертикалі
pdS - podS -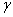 hdS = 0; hdS = 0;
| (2.2) |
p = po + h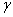 . .
| (2.3) |
Це і є основне рівняння гідростатики. Воно дозволяє обчислити тиск в будь-якій точці рідини, що знаходиться в стані спокою. З нього виходить, що шуканий тиск складається з тиску на вільній поверхні і тиску, обумовленого силою тяжіння вищерозміщених шарів рідини. Як видно з формули (2.3), тиск в рідині із зростанням глибини збільшується за лінійним законом. Позначивши через z координату т. А, через zо - координату вільної поверхні рідини і замінивши h на zо- z одержимо
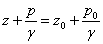
| (2.4) |
Оскільки точка А узята довільно, то можна стверджувати, що для всього об'єму рідини, що знаходиться в стані спокою
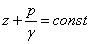
| (2.5) |
Це інший вираз основного рівняння гідростатики. Координата z називається нівелірною висотою і за фізичним смислом є питомою енергією положення рідини. Величина 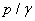 має також лінійну розмірність і називається п'єзометричною висотою, а за фізичним смислом є питомою енергією тиску.
має також лінійну розмірність і називається п'єзометричною висотою, а за фізичним смислом є питомою енергією тиску.
Таким чином, сума нівелірної і п'єзометричних висот або питомих енергій положення і тиску для будь-якої точки рідини, що перебуває у стані спокою, є величина постійна, і називається гідростатичним напором.
2.3. Диференціальне рівняння рівноваги рідини
Диференціальні рівняння рівноваги рідини можна одержати у разі, коли на рідину діє не тільки сила тяжіння, але й інші масові сили, наприклад, сили інерції переносного руху при так званому відносному спокої. У нерухомій рідині візьмемо довільну точку М з координатами x, у і z і тиском р. Виділимо в рідині елементарний об'єм у формі прямокутного паралелепіпеда з ребрами, паралельними координатним осям і відповідно рівними dx, dy і dz, а точка М буде однією з вершин виділеного паралелепіпеда (рис.2.3). Розглянемо умови рівноваги виділеного об'єму рідини. Хай у виділеному об'ємі на рідину діє результуюча масова сила, складові якої, віднесені до одиниці маси, рівні X, Y і Z. Тоді масові сили, що діють на виділений об'єм у напрямку координатних осей, будуть рівні цим складовим, помноженим на масу виділеного об'єму.
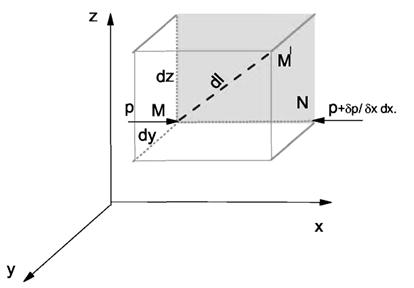
Рис. 2.3. До виводу диференціальних рівнянь рівноваги рідини
Тиск р є функція координат x, у і z, але поблизу точки М по всім трьом граням паралелепіпеда воно однакове, що витікає з доведеної вище властивості гідростатичного тиску. При переході від точки М, наприклад, до точки N змінюється лише одна координата х на нескінченно малу величину dx, у зв'язку з чим функція р одержує приріст, рівний часному диференціалу 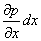 .
.
Тому тиск в точці N буде рівний  , де
, де 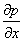 - градієнт тиску поблизу точки М у напрямку осі х.
- градієнт тиску поблизу точки М у напрямку осі х.
Розглядаючи тиск в інших відповідних точках граней, нормальних до осі х, наприклад, в точках N/ і M/ видно, що цей тиск різниться на однакову величину, рівну
 .
.
Зважаючи на це різниця сил тиску, що діють на паралелепіпед у напрямку осі х, буде рівна вказаній величині, помноженій на площу граней, тобто
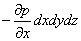 .
.
Аналогічним чином, але через градієнти тиску 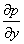 і
і  , виразяться різниці сил тиску, що діє на паралелепіпед у напрямку двох інших осей.
, виразяться різниці сил тиску, що діє на паралелепіпед у напрямку двох інших осей.
На виділений паралелепіпед діятимуть лише вказані масові сили і різниці тиску. Тому рівняння рівноваги паралелепіпеда у напрямку трьох координатних осей запишуться в такому вигляді
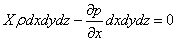
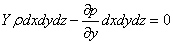
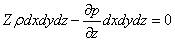
| (2.6) |
Розділимо ці рівняння на масу паралелепіпеда 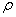 dxdydz і перейдемо до межі, спрямовуючи dx, dy і dz до нуля, тобто стягуючи паралелепіпед до початкової точки М. Тоді в межі одержимо рівняння рівноваги рідини, віднесені до точки М.
dxdydz і перейдемо до межі, спрямовуючи dx, dy і dz до нуля, тобто стягуючи паралелепіпед до початкової точки М. Тоді в межі одержимо рівняння рівноваги рідини, віднесені до точки М.
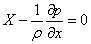

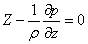
| (2.7) |
Система диференціальних рівнянь гідростатики називається рівняннями Ейлера.
2.4. Прикладні питання гідростатики
2.4.1. П'єзометрична висота
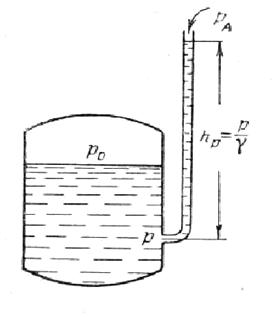
П'єзометрична висота, рівна 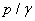 , є висотою стовпа даної рідині, відповідна даному тиску р (абсолютному або надлишковому). П'єзометричну висоту, відповідну надмірному тиску, можна спостерігати в так званому п'єзометрі показаному на рис.2.4, простому пристрої для вимірювання тиску. П'єзометр є вертикальною скляною трубкою, верхній кінець якої відкритий в атмосферу, а нижній приєднаний до того об'єму рідини, де вимірюється тиск.
, є висотою стовпа даної рідині, відповідна даному тиску р (абсолютному або надлишковому). П'єзометричну висоту, відповідну надмірному тиску, можна спостерігати в так званому п'єзометрі показаному на рис.2.4, простому пристрої для вимірювання тиску. П'єзометр є вертикальною скляною трубкою, верхній кінець якої відкритий в атмосферу, а нижній приєднаний до того об'єму рідини, де вимірюється тиск.
Застосовуючи формулу (2.3) до рідини, що міститься в п'єзометрі, одержимо
 ,
,
де рабс - абсолютний тиск в рідині на рівні приєднання п'єзометра; ра - атмосферний тиск.
Звідси висота підйому рідини в п'єзометрі рівна
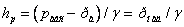
| (2.8) |
де рнад - надлишковий тиск на тому ж рівні.
| 
|
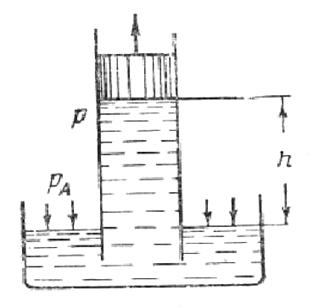
| Рис. 2.4. | Рис. 2.5. |
Очевидно, що якщо на вільну поверхню рідини, що перебуває в спокої, діє атмосферний тиск, то п'єзометрична висота для будь-якої точки даного об'єму рідини рівна глибині розташування цієї точки. Часто тиск в рідинах або газах чисельно виражають у вигляді відповідної цьому тиску п'єзометричної висоти за формулою (2.6).
Наприклад, одній технічній атмосфері відповідає:
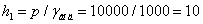 м.вод.ст.
м.вод.ст.
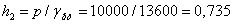 м.рт.ст.
м.рт.ст.
Якщо абсолютний тиск в рідині або газі менше атмосферного, то має місце розрядження або вакуум.
За величину розрядження береться різниця тиску
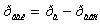 або
або 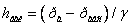
Як приклад, розглянемо трубу з щільно пригнаним до неї поршнем, з одного боку, а іншою стороною вона опущена в судину з рідиною (див. рис.2.5). Далі, поступово підніматимемо поршень вгору. Рідина слідуватиме за поршнем і разом з ним підніметься на деяку висоту Н від вільної поверхні з атмосферним тиском. Оскільки для точок, розташованих над поршнем, глибина їх занурення відносно вільної поверхні від’ємна, то згідно рівнянню (2.3) абсолютний тиск рідини під поршнем буде рівний
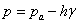
| (2.9) |
а величина вакууму 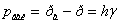 або
або 
У міру підйому поршня абсолютний тиск рідини над поршнем зменшуватиметься. Нижньою межею для абсолютного тиску рідини є нуль, а максимальне значення вакууму рівне атмосферному. При цьому, максимальна висота підйому рідини в даному прикладі (максимальна висота "всмоктування" рідини визначається з (2.9), якщо вважати, що p = 0, то матимемо  .
.
За нормального атмосферного тиску(1,033 кг/см2) висота hмах: для води 10,33 м, для бензину 13,8 м, для ртуті 0,76м і т.д.
Простим приладом для вимірювання вакууму може служити скляна трубка, показана на рис. 2.6 в 2-х варіантах. Вакуум в об'ємі рідини А, може вимірюватися або за допомогою U-подібної трубки (показана справа), або шляхом використання перевернутої U-подібної трубки, один кінець якої опущений в судину з рідиною (рисунок зліва).
2.4.3. Вимірювання тиску
Для вимірювання тиску рідин і газів в лабораторних умовах крім п'єзометрів використовують різні види манометрів, які діляться на рідинні і механічні.
Рідинні манометри залежно від конструкційних особливостей виконуються за різними схемами:
а) U-подібні;
б) послідовне з'єднання декілька v-образні манометрів;
в) чашковий манометр;
г) диференціальний v-образний манометр;
д) двохрідинний мікроманометр;
е) двохрідинний чашковий манометр.

Рис. 2.6. Прості вакуумметри
Механічні манометри бувають двох типів - пружинні або мембранні. Принцип їх роботи заснований на деформації порожнистої пружини або мембрани під впливом вимірюваного тиску, а через спеціальний механізм ця деформація передається стрілці, яка показує вимірюваний тиск на циферблаті. Розглянемо принцип роботи рідинних манометрів. Так званий U-подібний манометр (рис.2.7) є зігнутою скляною трубкою з ртуттю.

Рис. 2.7. Схеми рідинних манометрів
При вимірюванні невеликого тиску газу застосовують спирт воду і іноді тетраброметан. Якщо вимірюється тиск рідини і сполучна трубка заповнена цією рідиною, то потрібно враховувати висоту розташування манометра над т. М, тоді надмірний тиск в т. М. знайдемо за формулою
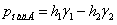 .
.
Послідовне з'єднання декількох U-подібних манометрів застосовується у випадку, якщо вимірюваний тиск рнад достатньо великий і відповідна йому висота h не уміщається в межах однієї U-подібної трубки.
Для двох таких трубок, показаних на рисунку 2.7, б ( К - кран або зажим для випуску повітря), маємо
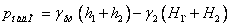 ,
,
або в загальному випадку для декількох трубок
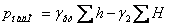
Чашковий манометр(рис.2.7, в) зручніший від попереднього тим, що користуючись ним потрібно фіксувати положення лише одного рівня рідини. При чималому діаметрі чашки порівняно з діаметром трубки рівень рідини можна вважати незмінним.
Диференціальний манометрслужить для визначення різниці тиску в двох точках, простим з яких є U-подібний манометр (рис.2.7, г). Якщо за допомогою такого манометра, що містить ртуть, проводиться вимірювання різниці тиску р1 і р2 в рідині з питомою масою 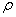 , яка повністю заповнює сполучні трубки, то
, яка повністю заповнює сполучні трубки, то 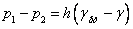 .
.
Двохрідинний чашковий манометр(рис.2.7, д) призначений для вимірювання тиску або розрядження повітря в інтервалі приблизно від 0,1 до 0,5 атм., тобто для випадку коли спиртовий або водяний манометр дає надмірно високий стовп рідини, і тому незручний для користування, а ртутний манометр не дає належної точності з причини недостатньої висоти стовпа ртуті.
Таким манометром користуються в швидкісних аеродинамічних трубах. Розглянемо принцип його роботи. У чашку заливається ртуть, а в трубку спирт, гас або інша рідина. Дуже зручним завдяки своїй малій випаровуваності є гас.
Відповідним підбором діаметрів верхньої і нижньої ділянок трубки (d1 і d2) можна одержати будь-яку ефективну питому вагу (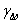 ), що входять у формулу
), що входять у формулу
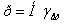 ,
,
де р - змінний тиск або розрядження; Н- показання манометра.
Знайдемо вираз для 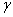 еф з таких рівнянь (див. рис. 2.7, е), рівняння рівноваги стовпів ртуті і керосину при р = ра
еф з таких рівнянь (див. рис. 2.7, е), рівняння рівноваги стовпів ртуті і керосину при р = ра
 ,
,
рівняння рівноваги при р > ра
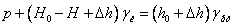
рівняння об'ємів (об'єм керосину, що перемістився з верхньої трубки d1 в нижню трубку d2, рівний об'єму витисненої ртуті)
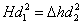 .
.
Провівши підстановки і перетворення, одержимо
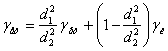
В транспортних машинах манометри застосовуються для контролю тиску масла в магістралях.
Найбільш поширеним типом манометра сьогодні є електричний манометр, рідше застосовуються механічні манометри. Як чутливий елемент в електричному манометрі використовується мембрана. Під впливом вимірюваного тиску мембрана деформується і через додатковий механізм примушує пересуватися движок потенціометра, який разом з покажчиком включений в електричну схему.
2.4.4. Сила тиску на плоску стінку
Обчислимо силу тиску Р, що діє з боку рідини на деяку ділянку даної стінки, обмежену довільним контуром і що має площу S (див. рис.2.8)
Вісь ОХ направимо по лінії перетину площини стінки з вільної поверхнею рідини, а вісь ОY- перпендикулярно цій лінії в площині стінки.
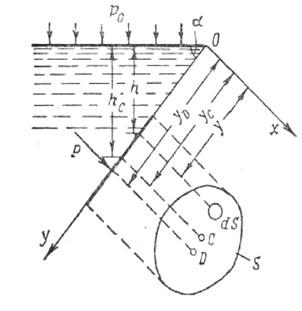
Рис. 2.8.
Елементарна сила тиску, прикладена до нескінченно малої площадки dS, визначається, як
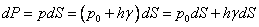 ,
,
де р0 - тиск на вільній поверхні; h - глибина розташування площадки dS.
Тоді для визначення повної сили Р виконаємо інтеграцію за всією площею S:
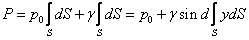 ,
,
де y- координата центру площадки dS.
Останній інтеграл, як відомо з механіки, є статичним моментом площі S відносно осі ОХ і рівний добутку цієї площі на координату її центра тяжіння (т.С), тобто 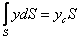
Отже, 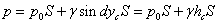 , де hc - глибина розташування центру тяжіння площі S, або
, де hc - глибина розташування центру тяжіння площі S, або
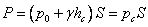
| (2.10) |
тобто повна сила тиску рідини на плоску стінку рівна добутку площі стінки на величину гідростатичного тиску в центрі тяжіння цієї площі. Коли тиск ро є атмосферним, то сила надмірного тиску рідини на плоску стінку рівна
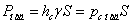
| (2.11) |
Визначимо положення центру тиску, тобто координату, точки перетину сили тиску рідини на стінку з площиною стінки.
Оскільки зовнішній тиск ро передається всім точкам площі S однаково, то рівнодіюча цього тиску буде прикладена в центрі тяжіння площі S. Для знаходження точки додатку сили надмірного тиску рідини (т. D) застосуємо рівняння механіки, смисл якого полягає в тому, що момент рівнодіючої сили тиску відносно осі ОХ рівний сумі моментів складових сил, тобто
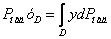 .
.
де yD - координата точки прикладання сили Рнад.
Виражаючи Рнад. і dРнад через ус і у і визначаючи уD,матимемо
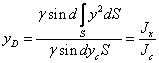 ,
,
де  – момент інерції площі S відносно осі ОХ.
– момент інерції площі S відносно осі ОХ.
Враховуючи, що 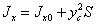 , де Jx0 – момент інерції площі S відносно центральної осі, паралельної ОХ. Тоді в остаточному вигляді одержимо
, де Jx0 – момент інерції площі S відносно центральної осі, паралельної ОХ. Тоді в остаточному вигляді одержимо
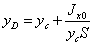
| (2.12) |
Таким чином, точка прикладання сили Рнад розташована нижче центру тяжіння площі стінки, а відстань між ними рівна
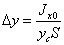 .
.
Якщо ро = ратм і воно діє з обох боків стінки, то точка D і буде центром тиску.
Коли ро є підвищеним, то центр тиску знаходиться за правилами механіки як точка прикладання рівнодіючій двох сил: hc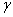 S і poS. Якщо poS > hc
S і poS. Якщо poS > hc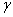 S, то центр тиску буде ближче до центру тяжіння площі S.
S, то центр тиску буде ближче до центру тяжіння площі S.
Для визначення іншої координати – ХD слід скласти рівняння моментів відносно осі ОY.
Окремий випадок.
Коли стінка має прямокутну форму, причому одна із сторін прямокутника співпадає з вільною поверхнею рідини, положення центру тиску знаходиться дуже просто. Оскільки епюра тиску рідини на стінку зображається прямокутним трикутником (див. рис.2.9), центр тяжіння якого знаходиться на 1/3 висоти в трикутнику, то і центр тиску рідини буде розташований на 1/3 висоті, рахуючи знизу.
У гідротехніці доводиться часто стикатися з дією сили тиску рідини на плоскі стінки, наприклад, на стінки робочих елементів різних гідростатичних споруд і пристроїв, при цьому тиск ро звично буває настільки високим, що центр тиску можна вважати співпадаючим з центром тяжіння площі стінки.

Рис. 2.9.
2.4.5. Сила тиску рідини на циліндричні і сферичні поверхні
Рішення задачі про силу тиску рідини на поверхні довільної форми в загальному випадку приводиться до визначення трьох складових сумарної сили і трьох моментів. У більшості випадків доводиться мати справу з циліндричними або сферичними поверхнями, що мають вертикальну площину симетрії. У таких випадках тиск рідини зводиться до рівнодіючої сили, лежачої в площині симетрії.
Візьмемо циліндричну поверхню АВ з твірною, перпендикулярною площині креслення (рис.2.10.), і визначимо силу тиску рідини на цю поверхню в двох випадках: рідина розташована зверху (а) і рідина розташована знизу (б).

Рис. 2.10. Тиск рідини на циліндричну поверхню
Випадок а): виділимо об'єм W рідини, обмежений даною поверхнею АВ, вертикальними поверхнями, проведеними через границі цієї ділянки, і вільною поверхнею рідині, тобто об'єм АВСD, і розглянемо умови його рівноваги у вертикальному і горизонтальному напрямках. Якщо рідина діє на поверхню АВ з силою Р, то поверхня АВ чинить на рідину такий же тиск, але направлений у протилежний бік. Силу реакції з боку поверхні в даному випадку, розкладемо на дві складові: горизонтальну Рг і вертикальну Рв.
Кутова рівновага об'єму АВСD у вертикальному напрямку має вигляд
| Рв = р0 Sr+G, | (2.13) |
де ро - тиск на вільній поверхні рідини; Sr - площа горизонтальної проекції поверхні АВ; G – тиск не виділеного об'єму рідини.
Умови рівноваги цього об'єму в горизонтальному напрямі запишемо з урахуванням того, що сили тиску рідини на поверхні ЕО і АD взаємно врівноважуються і залишається лише сила тиску на площу ВЕ, тобто вертикальну проекцію поверхні АВ – Sв
Pг = SB hc  +p0SB +p0SB
| (2.14) |
Визначивши по формулам (2.13) і (2.14) вертикальну і горизонтальну складові повної сили тиску Р, знайдемо цю силу

| (2.15) |
У тому випадку "б", коли рідина розташована знизу, величина гідростатичного тиску в усіх точках поверхні АВ має ті ж значення, що і у випадку "а", але напрямок його буде протилежним і сумарні сили Рв і Рг визначатимуться за тими ж формулами, але зі зворотним знаком.
При цьому, під величеною G слід розуміти так само як і у разі "а" всі рідини в об'ємі АВСD, хоча цей об'єм і не заповнений рідиною. Положення центру тиску на циліндричній стінці легко може бути знайдено, якщо відомі Рв і Рг і якщо визначений центр тиску на вертикальній проекції стінки або центр тяжіння виділеного об'єму АВСD. Завдання полегшується у тому випадку, коли дана поверхня є кругом, оскільки рівнодіюча сила при цьому перетинає вісь поверхні. Це витікає з того, що будь-яка сила тиску dP нормальна до поверхні, тобто направлена по радіусу. Викладений спосіб визначення сили тиску на циліндричні поверхні може бути застосований також, і до сферичних поверхонь, причому рівнодіюча сила в цьому випадку також проходить через центр поверхні і лежить у вертикальній площині симетрії.
2.4.6. Закон Архімеда
Застосуємо розглянутий прийом знаходження вертикальної складової сили тиску рідини на криволінійну стінку для доказу відомого закону Архімеда.
Розглянемо тіло прямокутної форми об'ємом W занурене в рідину (рис.2.11). Спроектуємо це тіло на вільну поверхню рідини і проведемо проектуючу циліндричну поверхню, яка торкається поверхні тіла на замкнутій кривій. Ця крива визначає верхню частину поверхні АСВ від нижньої АDВ. Вертикальна складова сили надмірного тиску рідини на верхню частину поверхні тіла Рв направлена вниз і рівна вазі рідини в об'ємі А В
В СА. Вертикальна складова сили тиску рідини на нижню частину поверхні тіла Рв2 направлена вгору і рівна вазі рідини в об'ємі А
СА. Вертикальна складова сили тиску рідини на нижню частину поверхні тіла Рв2 направлена вгору і рівна вазі рідини в об'ємі А В
В DA. Звідси витікає, що вертикальна складова сили тиску рідини на тіло буде направлена вгору і рівна вазі рідини в об'ємі, рівному різниці вказаних двох об'ємів, тобто в об'ємі тіла РА = РВ1 –РВ1 = GABCD = W.
DA. Звідси витікає, що вертикальна складова сили тиску рідини на тіло буде направлена вгору і рівна вазі рідини в об'ємі, рівному різниці вказаних двох об'ємів, тобто в об'ємі тіла РА = РВ1 –РВ1 = GABCD = W.

Рис. 2.11. До доказу закону Архімеда
У цьому і полягає закон Архімеда, що звично формулюється так: тіло, занурене в рідину, втрачає в своїй вазі стільки, скільки важить витиснена ним рідина. Закон Архімеда, зрозуміло, справедливий і для тіл, частково занурених у рідину.
Залежно від співвідношення сили ваги тіла G і архімедової сили Ра можливі три випадки:
1) G > Ра - тіло тоне;
2) G < Ра - тіло спливає;
3) G = Ра - тіло плаває.
Для рівноваги плаваючого тіла, крім рівності сил G = Ра, необхідне ще рівність нулю сумарного моменту. Остання умова виконується тоді, коли центр тяжіння тіла лежить на одній вертикалі з центром водотоннажності.
Тема 3. ОСНОВИ ГІДРОДИНАМІКИ
3.1. Основні поняття.
3.2. Рівняння нерозривності руху.
3.3.Рівняння нерозривності руху в диференціальній формі.
3.4. Рівняння Бернуллі.
3.1. Основні поняття
Гідродинамікою називається розділ механіки суцільних середовищ, що вивчає закономірності руху рідини і її взаємодію із зануреними в неї тілами. Основним допущенням є те, що рідина є суцільною сферою навіть при нескінченно малих об'ємах. Рідина складається з нескінченно великого числа частинок рідини, фізичний образ при розгляді рівнянь руху рідини представляється як нескінченно мала маса рідини, що займає нескінченно малий об'єм.
Переходячи до вивчення питань руху рідини, ми розглядатимемо рух так званої ідеальної рідини.
Ідеальною рідиною (газом) називається нев'язка теплопровідна рідина (газ), при тиску якої виникають тільки нормальні напруження. Рух рідини може бути сталим (стандартним) або несталим (нестандартним).
Сталий рух - це течія, незмінна за часом, при якій тиск і швидкість є функціями лише координат, але не залежать від часу.
Математично це можна записати так:
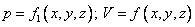 ;
;
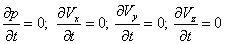
| (3.1) |
Індекси у швидкості означають проекції цієї швидкості на відповідні осі, жорстко пов'язані з руслом.
Несталий рух - це течія, при якій тиск і швидкість залежать як від координат, так і від часу, тобто.
| p=F1(x, у, z, t); V=F2(x, у, z, t) | (3.2) |
Приклади несталої течії:
– поступове спорожнення судини через отвір в дні або рух рідини у всмоктуючій або напірній трубі простого поршневого насоса.
– Прикладами сталого перебігу рідини можуть бути:
– витікання рідини з судини, в якій підтримується постійний тиск;
– рух рідини в замкнутому трубопроводі, що створюється роботою відцентрового насоса з постійним числом оборотів.
При сталому русі траєкторії різних частинок, що проходять через дану точку простору, матимуть різну форму. Тому при розгляді картини течії, що утворюється в кожен даний момент часу, вводиться поняття лінії току.
Траєкторія - лінія, що описується рухомою частинкою з часом. Лінією токуназивається така лінія в рухомій рідині, дотичні до якої в будь-якій її точці співпадають з напрямком векторів швидкості частинок, розташованих на цій лінії в даний момент часу (рис.3.1).
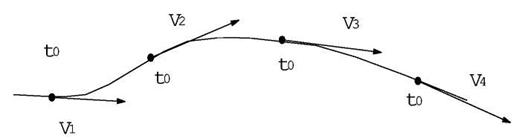
Рис. 3.1. Лінія току
Якщо в рухомій рідині узяти елементарний замкнутий контур і через всі його точки провести лінії току, то утворюється трубчаста поверхня, що називається трубкою току. Частина потоку, розміщена усередині трубки току, називається цівкою (рис.3.2).
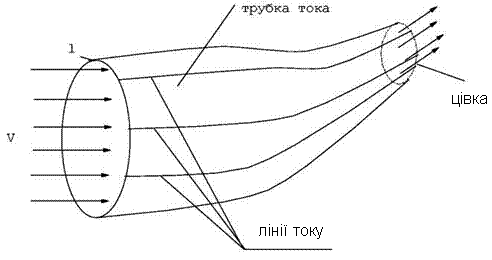
Рис. 3.2. Структура елементарного контуру
Перетином потоку називається поверхня в межах потоку, проведена нормально до лінії току.
Розрізняють рух рідини напірний і безнапірний.
Напірним називають рух в закритих руслах без вільної поверхні, а безнапірними - рух з вільною поверхнею. Приклади напірного руху - рух в трубопроводах з підвищеним (або зниженим) тиском. Безнапірний рух - рух у річках, відкритих каналах і лотках.
3.2. Рівняння нерозривності руху рідини
Рівняння нерозривності є математичним виразом фундаментального закону природи про збереження маси рухомої рідини або газу, якщо передбачається відсутність в потоці розривів і порожнеч. При виведенні рівняння розглядається середовище, що стискається, рух потоку в загальному випадку є несталим.
Виділимо в потоці зафіксований елементарний об'єм у формі паралелепіпеда із сторонами dx, dy, dz (рис. 3.3).

Рис. 3.3.
Визначимо зміну маси в даному об'ємі за час dt. Уздовж осі ОХ за час dt у виділений паралелепіпед втікає маса газу  , а витікає
, а витікає 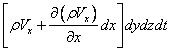 .
.
Зміна маси газу усередині виділеного об'єму уздовж осі ОХ за час dt рівне

| (3.3) |
Аналогічно уздовж осей OY і OZ
 ;
;

| (3.4) |
Повна зміна маси усередині виділеного об'єму буде
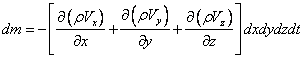
| (3.5) |
З іншого боку, зміна маси рідини відбувається за рахунок зміни густини за час dt, тобто
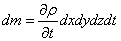
| (3.6) |
Прирівнявши відповідні вирази і скоротивши на dxdydzdt одержимо
Це і є рівняння нерозривності в диференціальній формі, справедливе в загальному випадку несталого руху середовища, що стискається, за умови його суцільності.
Розглянемо деякі окремі випадки рівняння нерозривності:
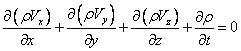
| (3.7) |
а) якщо течія стала, тобто параметри рідини з часом не змінюються, то 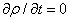 і рівняння набуває вигляду
і рівняння набуває вигляду
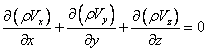
| (3.8) |
б) для несталого руху нестискуваної рідини (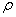 = const)
= const)

| (3.9) |
Якщо ж течія до того ж потенціальна, то рівняння (3.9) має вигляд
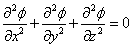
| (3.10) |
Таке рівняння носить назву рівняння Лапласа.
в) для цівки кінцевих розмірів з площами поперечного перетину S1, S2 і т.д. (рис. 3.4) рівняння нерозривності при сталому перебігу можна виразити у вигляді рівності маси речовини, що проходить через будь-яке поперечне січення в одиницю часу

| (3.11) |

Рис. 3.4.
Витратою називається кількість рідини, що протікає через поперечний перетин потоку в одиницю часу. Розрізняють витрати об'ємні Q, вагові G і масові М.
| Елементарні об'ємні витрати dQ = VdS, м3 | (3.12) |
Елементарні вагові витрати dG = 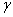 dQ,Н/с dQ,Н/с
| (3.13) |
Елементарні масові витрати dM = 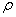 dQ, кr/c dQ, кr/c
| (3.14) |
Для отримання рівняння витрати виділимо в точці елементарну цівку (див. рис.3.4). Площа її поперечного перетину - dS. На підставі закону збереження речовини можна записати:
| dQ=V1 dS1 = V2 dS2 = V3 dS3= const, | (3.15) |
або, враховуючи постійність маси рідини і переходячи від цівки до потоку кінцевих розмірів
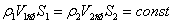
| (3.16) |
де V1cp, V2cp - середня по перетину швидкість.
Оскільки в гідравліці рідина вважається практично нестискуваною, то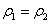 і тоді
і тоді
| V1cp S1 = V2cp S2 = const або V1cp/V2cp = S2/S1 | (3.17) |
Висновок: середня швидкість в потоці нестискуваної рідини обернено пропорційна площі перетину потоку.
3.3. Рівняння руху в диференціальній формі
Рівняння руху нев'язкої рідини (газу) виражають собою закон збереження кількості руху стосовно цівки ідеальної рідини. Виділимо в рідині в деякий момент часу елементарну частинку у формі паралелепіпеда з ребрами dx, dy, dz і гранями, паралельними координатним площинам (рис.3.5).

Рис. 3.5.
Маса виділеної частинки рівна 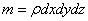
| (3.18) |
Хай V - поступальна швидкість частинки, F - сумарна зовнішня сила, що діє на неї.
| Згідно з законом про зміну кількості руху mdV = Fdt | (3.19) |
У проекції на вісь OX одержимо 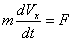 . .
| (3.20) |
Зовнішня сила, що діє на виділену частинку уздовж осі OX, складається з сил тиску і інерційних сил, пропорційних масі. Різниця сил тиску уздовж осі OX буде рівна

| (3.21) |
Інерційну силу уздовж осі OX можна представити як добуток маси m на прискорення jx, що діє уподовж цієї осі. Тоді з урахуванням виразу для маси (3.18) сила Fx буде рівна
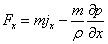
| (3.22) |
Розділивши обидві части рівняння (3.22) на m з урахуванням (3.20) одержимо
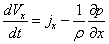
| (3.23) |
Аналогічно вздовж інших осей

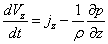
| (3.24) |
Рівняння (3.23, 3.24) вперше були одержані Л. Ейлером і називаються його ім'ям. У деяких окремих випадках диференціальне рівняння Ейлера можуть бути проінтегровані, що дає можливість виявити важливі закономірності в залежностях між параметрами рідини. Одним з окремих рішень є рівняння збереження енергії (рівняння Бернуллі)
3.4. Рівняння Бернуллі
3.4.1. Рівняння Бернуллі для цівки ідеальної рідини
У цівці ідеальної рідини тертя відсутнє і швидкість потоку по перетину постійна, тобто 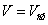 .
.
Приймемо наступні допущення:
– рідина ідеальна (нев'язка, нестискувана);
– потік сталий.
У цівці ідеальної рідини виділимо перетинами 1 і 2 ділянку довільної довжини (рис.3.4). За нескінченно малий відрізок часу dt, виділена ділянка переміститься в положення 1/-2/ .
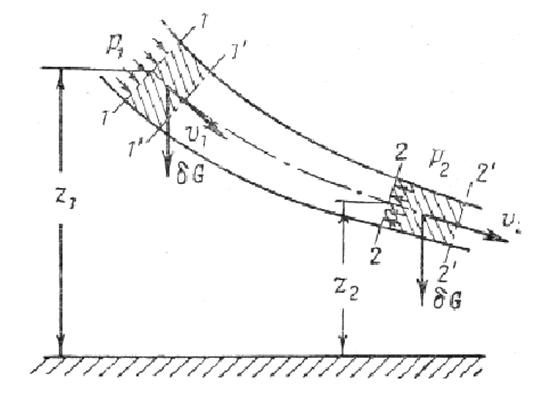
Рис. 3.4. До виводу рівняння Бернуллі для цівки
На підставі закону збереження енергії можна записати, що зміна кінетичної енергії елементарного об'єму рідини при його русі від перетину 1-1 до перетину 2-2 рівна зміні потенційної енергії, що забезпечується нівелірною висотою z і тиском р.

| (3.25) |
Розділивши обидві части рівняння (3.25) на dG (елементарна вагова витрата)одержимо
 , або , або 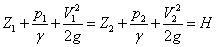
| (3.26) |
де Z1, Z2 - нівелірна висота або питома енергія положення (геометричний напор);
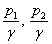 - п'єзометрична висота або питома енергія тиску (п’єзометричний напор);
- п'єзометрична висота або питома енергія тиску (п’єзометричний напор);
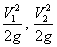 - швидкісна висота або питома кінетична енергія (швидкісний напор); Н - повна питома енергія.
- швидкісна висота або питома кінетична енергія (швидкісний напор); Н - повна питома енергія.
Дане рівняння (3.26) було вперше одержано Данилом Бернуллі в 1738 році і виражає собою закон збереження механічної енергії.
Висновок по рівнянню:сума питомих енергій положення, тиску і кінетичного або геометричного, п'єзометричного і швидкісного напорів в будь-якому перетині сталого потоку ідеальної рідини є величиною постійною, що дорівнює повній питомій енергії або повному напору.
3.4.2. Рівняння Бернуллі для реального потоку
Реальний потік відрізняється від ідеального тим, що розподіл швидкостей по перетину потоку нерівномірний і потік в'язкий, тобто існують втрати енергії уздовж потоку за рахунок його гальмування під впливом в'язкості, а також дії сил молекулярного зчеплення між рідиною і стінкою. Швидкість досягає найбільшої величини в центральній частині потоку, а у міру наближення до стінки зменшується практично до нуля (рис.3.5).

Рис. 3.5. Розподіл швидкостей в потоці
Допущення: вважаємо, що в межах кожного перетину потоку справедливе основне рівняння гідростатики:  = const (при струменевій течії це виконується і може бути строго доведене).
= const (при струменевій течії це виконується і може бути строго доведене).
Тоді питома потенційна енергія і для реального потоку визначається сумою  .
.
Кінетична енергія для цівки буде
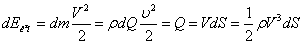
| (3.27) |
Для всього потоку
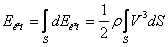
| (3.28) |
Питома кінетична енергія
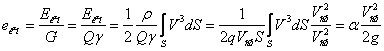
| (3.29) |
де 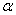 - коефіцієнт Коріоліса, рівний відношенню питомої кінетичної енергії реального потоку до питомої кінетичної енергії, обчисленої за середньою в даному перетині швидкістю
- коефіцієнт Коріоліса, рівний відношенню питомої кінетичної енергії реального потоку до питомої кінетичної енергії, обчисленої за середньою в даному перетині швидкістю
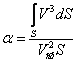
| (3.30) |
Завжди 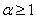 . Тоді середнє по перетину значення повної питомої енергії буде
. Тоді середнє по перетину значення повної питомої енергії буде
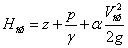
| (3.31) |
Очевидно Нср.2 < Нср1. Дійсно, через в'язкість виникають напруження тертя між шарами рідини. Це призводить до нерівномірності швидкостей по січенню івихороутворенню. На це витрачається енергія і тому середнє значення повної питомої енергії уздовж потоку зменшується. Можна сказане записати:
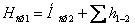 або або 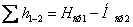 , ,
| (3.32) |
де 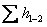 - сумарна втрата питомої енергії проштовхування рідини між перетинами на ділянці 1-2. Ці втрати називаються гідравлічними.
- сумарна втрата питомої енергії проштовхування рідини між перетинами на ділянці 1-2. Ці втрати називаються гідравлічними.
Таким чином, рівняння Бернуллі для реального потоку матиме вигляд:
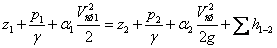
| (3.33) |
Графічне представлення рівняння Бернуллі
На рис.3.6 показана цівка рідини, площа поперечного перетину якої від перетину 1-1 до перетину 2-2 зменшується, а потім від перетину 2-2 до перетину 3-3 збільшується.
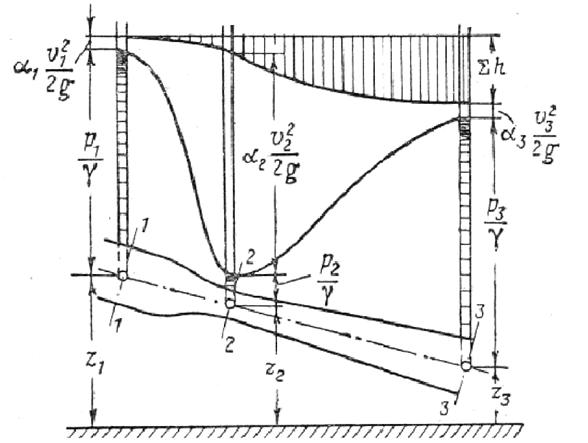
Рис. 3.6. Графічна ілюстрація рівняння Бернуллі для реального потоку
Оскільки з рівняння Бернуллі і рівняння витрати виходить, що якщо площа поперечного перетину цівки зменшується, тобто цівка звужується, то швидкість руху рідини збільшується, а тиск зменшується (перетин 2-2), і навпаки, якщо цівка розширюється, то швидкість зменшується, а тиск зростає (перетин 3-3). В'язкість же грає наступну роль: створюючи сили тертя між шарами, міняє їх швидкість по перетину, тим самим збільшує кінетичну енергію потоку при незмінній середній швидкості перетину.
Висновок: для цівки ідеальної рідини рівняння Бернуллі є законом збереження енергії. Для реального потоку рівняння Бернуллі є рівнянням балансу енергії з урахуванням втрат.
Енергія, що втрачається на ділянці течії, перетворюється на іншу форму -теплову, яка безперервно розсіюється, тому підвищення температури практично мало помітно. Цей процес є необерненим.
Тема 4. ГІДРАВЛІЧНІ ОПОРИ
4.1. Режими руху рідини.
4.2. Лінійні втрати напору при русі рідини.
4.3. Місцеві втрати напору при русі рідини.
4.1. Режими руху рідини
У гідравліці розрізняють такі основні режими руху рідини: ламінарний, турбулентний і кавітаційний.
Ламінарний(шаруватий) рух характерний тим, що частинки рідини рухаються у своїх шарах не перемішуючись (рис. 4.1).

Рис. 4.1. Характер ліній струму в ламінарному потоці
Дотичне напруження, що виникає при ковзанні шарів рідини, підпорядковується закону Ньютона.
 , н/м2. , н/м2.
| (4.1) |
При ламінарному русі відбувається поступальний і обертальний рух частинок. Течія є строго сталою. Лінії току паралельні осі трубки. Перемішування шарів рідини не відбувається.
Турбулентна течіясупроводжується інтенсивним перемішуванням рідини і пульсацією швидкостей і тиску. Течія, строго кажучи, нестала. Вважатимемо течію сталою умовно користуючись Vуср. На відміну від Vср за перетином, Vуср усереднюється за величиною. Дотичне напруження визначається за формулою:
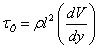
| (4.2) |
де l - усереднена за часом вертикаль переміщення частинок.
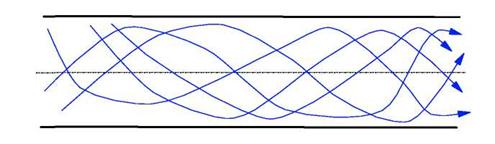
Рис. 4.2. Характер ліній току в турбулентному потоці
Разом з подовжнім переміщенням потоку відбувається поперечний і обертальний рух окремих об'ємів.
У 1883 році Рейнольдс встановив, що перехід від ламінарної течії до турбулентної залежить від в'язкості і характерного розміру - діаметру трубопроводу. Зміна режимів відбувається при певній швидкості, яка називається критичною, при цьому її значення визначається із співвідношення
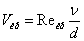
| (4.3) |
де Rекр - критичне число Рейнольдса (Rе- критерій подібності, що характеризує в'язкість рідини); v - кінематична в'язкість.
Дослідами встановлено, що для рідин Rекр = 2300. Тому про характер течії можна судити за фактичним значенням числа Rе, виражаючи його через фактичну швидкість.
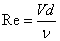
| (4.4) |
Якщо Rе < Rекр - течія ламінарна, при Rе 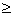 Rекр - течія турбулентна.
Rекр - течія турбулентна.
При русі рідини в трубах іноді відбуваються явища, пов'язані з виділенням розчинених в рідині газів і з перетворенням рідини в пару.
Кавітаційнийрежим течії (кавітація) - це місцеве закипання рідини, обумовлене місцевим падінням тиску в потоці з подальшою конденсацією пари у області підвищеного тиску (рис.4.3).
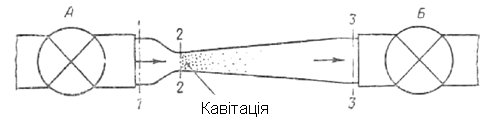
Рис. 4.3. Схема трубки для демонстрації кавітації
Розглянемо рух рідини через місцеве звуження. Позначимо через рм - місцевий тиск у вузькому перетині. Швидкість в перетині 2-2 збільшена порівняно з перетином 1-1, тому рм<р впорівнянні з перетином 1-1.
Якщо швидкість течії (витрата) в трубопроводі збільшиться, то тиск у вузькому перетині впаде ще більше. При цьому, якщо рм > рt, то течія буде без особливостей (рt - тиск насиченої пари). Якщо рм = рt, то у вузькому місці почнеться місцеве кипіння рідини. У частині, що розширюється, швидкість зменшується, тиск зростає, кипіння припиниться.
Кавітація супроводжується характерним шумом - "бубнінням", а при тривалій дії призводить до ерозії стінок труби, причому ерозія відбувається не в місці утворення бульбашок, а в місці їх конденсації. У гідротехнічних системах кавітація може виникнути у зв'язку із зменшенням зовнішнього тиску. Потік при цьому стає двофазним, що складається з рідкої і парової фаз. При цьому можуть спостерігатися різні схеми потоків (рис.4.4).
а) малобульбашкова;
б) крупнобульбашкова;
в) з розділенням рідкої і парової фаз;
г) з утворенням парових пробок.

Рис. 4.4. Схеми потоків рідини з повітрям
Для боротьби з кавітацією прагнуть виключити різкі звуження трубопроводів, а в баках створюють додаткове підтискування. Кавітація характеризується коефіцієнтом 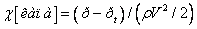
Кавітація починається при 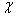 =0. Шкідливі наслідки кавітації:
=0. Шкідливі наслідки кавітації:
– погіршення гідравлічних характеристик дросельних пристроїв;
– ерозії каналів;
– деструкції присадки гідравлічних рідин;
– коливань тиску.
Широкі дослідження кавітації створюють передумови для використання її в практичних цілях. Кавітаційні пристрої, засновані на явищі стабілізації витрат, використовуються як регулятори подачі палива тощо. Ефект гідродинамічної кавітації використовується для очищення деталей від забруднення і для дроблення частинок забруднювача. При промивці моделей з органічного скла досягається повне видалення забруднень з тупикових поверхонь завдовжки 8-10 метрів.
4.2. Лінійні втрати напору при русі рідини
4.2.1. Ламінарний рух рідини
Теорія ламінарного руху рідини ґрунтується на законі тертя Ньютона
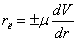 ,
,
Знаки " ± " означають, що дотичні напрями в сусідніх шарах однакові по величині, але протилежно направлені. Для отримання виразів по обчисленню параметрів ламінарного потоку розглянемо сталу течію в круглій прямій трубі радіусу r0, розташованій горизонтально (рис. 4.5).
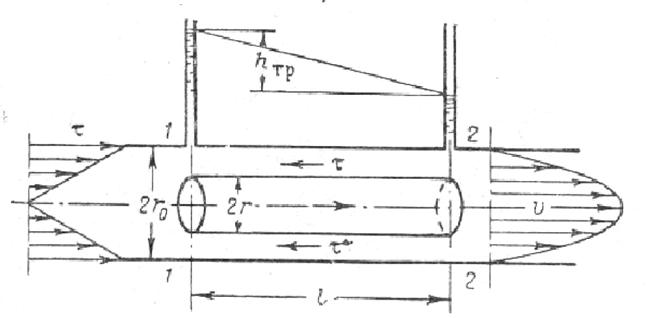
Рис. 4.5. До теорії ламінарного руху рідини в трубі
Для цього випадку z1 = z2 і Vcp = f(l) = соnst. В цьому випадку рівняння Бернуллі набуває вигляду:

| (4.5) |
Звідси втрати на тертя

| (4.6) |
Виділимо в потоці рідини циліндричний об'єм радіусом r і завдовжки l, співісний з трубою. Умовою його рівноваги є рівність нулю суми сил нормального тиску, що діють на торці виділеного об'єму, і сил тертя, що діють уподовж його бічної поверхні. Отже,
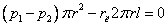
| (4.7) |
Звідси
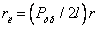
| (4.8) |
Висновок: при ламінарному русі дотичне напруження за радіусом трубопроводу змінюється по лінійному закону. Швидкість при цьому з урахуванням 4.1 і 4.8
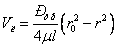
| (4.9) |
Тобто швидкість змінюється пропорційно квадрату радіусу. Оскільки елементарна витрата dQ = VdS, то сумарна витрата в трубопроводі
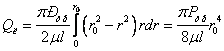
| (4.10) |
Звідси можна визначити середню швидкість

| (4.11) |
Порівнюючи (4.11) з (4.8) при r = 0 одержимо, що

| (4.12) |
Визначивши питому кінетичну енергію за фактичною швидкістю з урахуванням (4.9) і порівнюючи її з питомою кінетичною енергією, визначеною по середній швидкості, одержимо

| (4.12) |
Втрати напору на тертя, виражені через витрату, визначаються залежністю

| (4.14) |
Висновок: при ламінарній течії в круглій трубі втрати напору на тертя пропорційні витраті рідини і в'язкості і обернено пропорційні діаметру в четвертому ступені.
Втрати на тертя можна виразити і через швидкість
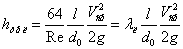
| (4.15) |
де  = 64/Rе - коефіцієнт опору тертя при ламінарній течії (погонний).
= 64/Rе - коефіцієнт опору тертя при ламінарній течії (погонний).
Вираз (4.15) відомий як формула Дарсі. Викладена теорія ламінарного руху рідини в круглій трубі добре підтверджується практикою у всіх випадках, за виключенням:
– У початковій ділянці труби, де відбувається поступове встановлення параболічного профілю швидкостей.
– При течії із значним теплообміном, тобто при русі рідини з нагріванням або охолоджуванням.
– За дуже великих перепадів тиску (р > 300 кгс/см2 = 300 105 Па), коли в’язкість залежить від тиску.
4.2.2. Поняття про початкову ділянку
Читайте також:
- Загальними мотивами, що спонукають фірми брати участь у міжнародному бізнесі, є можливість розширення продажу, придбання нових джерел ресурсів, диверсифікація.
- Заняття ф.в. у межах розширення активного відпочинку.
- Здатність до стиску та температурне розширення
- Землетруси – це раптове звільнення потенціальної енергії земних надр, яка у вигляді ударних хвиль та пружних коливань (сейсмічні хвилі) розповсюджується в землі у всіх напрямках
- Зміна висоти голосу, тобто розширення його діапазону
- Зміною в ціннісній пропозиції товару або послуги може бути абсолютно новий товар або послуга або ж розширення існуючої пропозиції.
- Князювання Святослава (964—972 рр.) — сина Ольги й Ігоря — було спрямовано в основному на розширення кордонів Русі і збройну боротьбу із сусідами.
- Необхідність розширення множини цілих чисел.
- Обмежувальні розширення сертифіката
- Плавне звуження русла - конфузор
- Плавне розширення русла - дифузор
- Поворот русла
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 1. ВВЕДЕННЯ | | | Плавне розширення русла - дифузор |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |