• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Довірчі інтервали для параметрів нормального розподілу

Часто інженеру або досліднику треба подати інформацію про розподіл випад­кової величини через декілька параметрів, що цей розподіл описують. Навіть тоді, коли невідома формула функції або щільності розподілу, корисно обчислити головні покажчики на базі тих даних, що одержані у експерименті.

Параметри статистичного розподілу є емпіричними аналогами відповідних те­оретичних параметрів і служать їх точковими оцінками (точковою називають оцін­ку, що визначається одним числом). Для МХ оцінкою є , для DХ - S².

Точкові оцінки повинні бути незміщеними. Незміщеноюназивають статисти­чну оцінку q^* , якщо її математичне сподівання дорівнює оцінюваному параметру q при будь-якому об'ємі вибірки, тобто

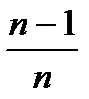M(q^*)=q ;M =MX; MS²= DX.

Вибіркове середнє та виправлена дисперсія , - незміщені оцінки.

Незміщена оцінка може давати добре, а може і не зовсім добре наближення до оцінюваного параметра; треба щоб і дисперсія величини, що оцінюється була ма­лою.

Ефективною називають статистичну оцінку, яка при заданому об'ємі вибірки n має найменшу можливу дисперсію. Оцінки , 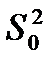являються ефективними.

Спроможною називають оцінку, яка при прямує по ймовірності до па­раметра, що оцінюється. Спроможність оцінок , 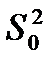означає, що для будь-якого

>0

; .

Теорія математичної обробки даних має у своєму арсеналі два принципи оцін­ки невідомих параметрів розподілу: точкове та інтервальне оцінювання. Недолік то­чкових оцінок у тому, що невідомо, з якою точністю вони визначають шуканий па­раметр. Якщо для великого числа спостережень (об'єму вибірки) точність звичайно буває достатньою для практичних висновків (у силу незміщеності, ефективності і спроможності), то для вибірок невеликого об'єму питання про точність оцінок яв­ляється вельми істотним. Це свідчить про можливість другого підходу, зв'язаного з інтервальними оцінками.

Нехай q - шуканий параметр розподілу, а q^*- його точкова оцінка, знайдена за даними досліду. Чим менше різниця |q-q^*|, тим краще якість оцінки, тим точніша оцінка. Точність оцінки характеризується числом таким, що |q^*--q^*|< . Параметр q невідомий, тому при заданому ставиться питання лише про ймовірність події

|q-q^*|<

Довірчою ймовірністю або надійністю називають ймовірність виконання нерівності |q-q^*|< і позначають 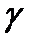, тобто

(11.1)

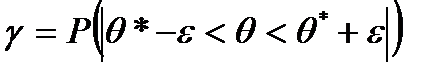
Звичайно надійність 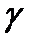задається; часто покладають:

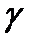= 0,9; 0,95; 0,99; 0,9973.

Формула (11.1) означає, що з ймовірністю 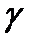параметр q попадає у інтервал (q *- ; q *+ ). Цей інтервал називають довірчим інтервалом. Іншими словами, 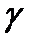- ймовірність того, що інтервал покриває невідомий параметр q.

Довірчий інтервал для математичного сподівання нормальної випадкової ве­личини при відомому середньому квадратичному відхиленні s:

Так, як X ~ N (a;s²), то . Дійсно, сума нормально розпо­ділених величин нормально розподілена і

, (так як всі X і мають розподіл X),

,

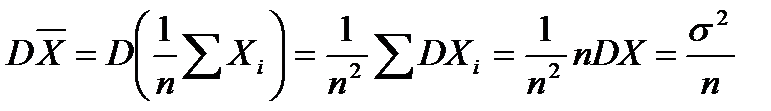Якщо σ – відоме, α – невідоме, то

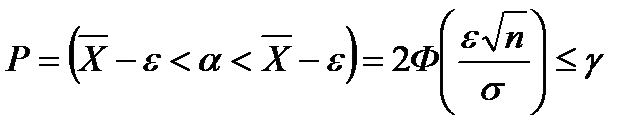
Якщо t – розв'язок рівняння 2Ф (t) = 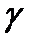, то довірчий інтервал надійності 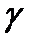для параметра α приймає вигляд:

Так як 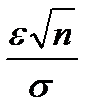= t, то = , де – точність оцінки.

Довірчий інтервал для математичного сподівання нормальної випадкової ве­личини при невідомому σ має вигляд:

,

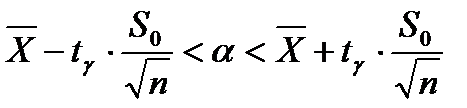де 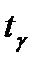– критичні точки так званого розподілу Стьюдента з (n - 1) степенями свобо­ди, а S₀ – корінь квадратний з виправленої вибіркової дисперсії.

Довірчий інтервал для середнього квадратичного відхилення нормальної випад­кової величини.

Нехай за вибіркою об'єму n знайдена виправлена дисперсія 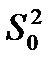. Тоді інтер­вал має вигляд:

(1 - q) · S₀ < σ < (1 + q) · S₀, для q < 1;

0 < σ < (1 + q) · S₀, для q > 1.

Де q – визначається за таблицею значень q = q ( 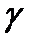, n) (див. додатки).

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
3. Автоматизація водорозподілу з комбінованим регулюванням
4. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
5. Автоматизація водорозподілу регулювання зі сталими перепадами
6. Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
7. Автоматизація водорозподілу регулюванням за верхнім б'єфом
8. Автоматизація водорозподілу регулюванням за нижнім б'єфом
9. Аналіз ефективності використання каналів розподілу
10. Аналіз розподілу прибутку підприємства
11. Аналіз розподілу прибутку.
12. Аналіз розподілу чистого прибутку.

Переглядів: 1490