• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Багатоканальна передача інформації

Розглянуті аналогові і цифрові сигнали повідомлення можуть бути використані для передачі по лінії зв'язку одночасно тільки одного повідомлення. Такий зв'язок називається одноканальним. Для того щоб зробити зв'язок багатоканальним, інформацію перед передачею ущільнюють. Існує два способи ущільнення інформації: ущільнення за часом і частотне ущільнення.

При ущільненні за часом кожен канал передачі інформації в межах загального часу роботи лінії зв'язку має дуже короткі проміжки часу, протягом яких інформація у вигляді коротких пакетів імпульсів передається від певного кореспондента відповідному абонентові. Передача інформації по каналах відбувається почергово в режимі розподілу часу. Частота перемикання каналів згідно з теоремою відліків моє бути вдвічі вищою від найвищої частоти спектра сигналу. Керування перемиканням каналів, тобто часова вибірність каналів зв'язку, виконується за допомогою спеціалізованих комп'ютерів.

Частотне ущільнення забезпечується лінійним перенесенням спектра сигналу повідомлення в область радіочастот. Кожне повідомлення в цьому разі передається по своїй носійній частоті, один з параметрів якої змінюється за законом зміни сигналу повідомлення. Таке перетворення носійного коливання називається модуляцією. На приймальному кінці каналу зв’язку радіосигнал зазнає оберненого перетворення — демодуляції, внаслідок чого одержують вихідний спектр сигналу повідомлення. Вибірність сигналів при частотному ущільненні здійснюється частотними фільтрами, настроєними на носійні частоти модульованих коливань.

У простому гармонічному коливанні

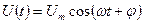(1.10)

можна змінювати три незалежних параметри: амплітуду , частоту 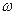і фазу . Відповідно одержують амплітудну (AM), частотну (ЧМ) і фазову (ФМ) модуляції. При використанні імпульсних і кодових сигналів застосовують інші, складніші види модуляції.

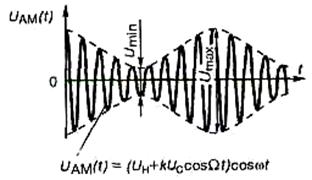
Амплітудна модуляція була запропонована ще в перші роки розвитку радіоелектроніки як найпростіше й очевидне вирішення проблеми багатоканальності. Саме цей вид модуляції розглядається при вивченні принципів радіозв’язку в курсі фізики середньої школи. З’ясуємо властивості АМ на спрощеній моделі: носійне високочастотне гармонічне коливання з частотою (рис.1.5, а) модулюється детермінованим гармонічним тональним коливанням з частотою (рис.1.5, б).

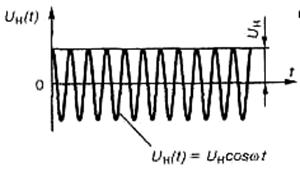
а

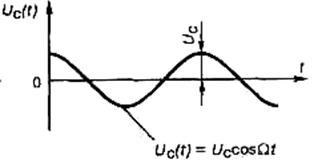
б

в

Рис. 1.5. Спрощена графічна модель амплітудно-модульованого сигналу

Для спрощення математичних викладок розглянемо парну косинусоїдну функцію без початкової фази

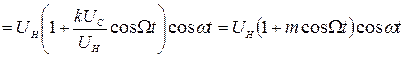, (1.11)

де 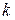— коефіцієнт пропорційності; — коефіцієнт AM, що дорівнює відношенню максимальної зміни амплітуди модульованого сигналу до його середнього значення.

Цей вираз при використанні відомої тригонометричної тотожності

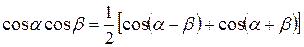легко перетворюється на вираз

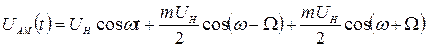. (1.12)

Для практичного визначення коефіцієнта модуляції з осцилограми (рис. 1.5, в) зручно користуватися таким виразом:

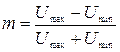. (1.13)

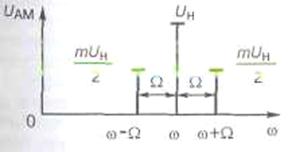
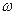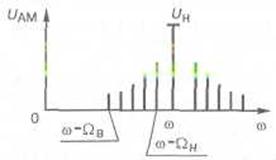
Як випливає з (1.12), напруга модульованого сигналу є сумою трьох високочастотних гармонічних коливань. Одне з них — носійне з частотою ; два інших розташовуються симетрично відносно носійного коливання на осі частот, відповідно вище і нижче нього на частоту (рис. 1.6, а). Ці коливання називають бічними складовими модульованого сигналу. Амплітуда бічних коливань не може перевищувати половини амплітуди носійного коливання, оскільки згідно з (1.13) коефіцієнт модуляції не може бути більшим за 1. Якщо модулювальний сигнал має кілька складових, то відповідно бічні частоти перетворюються на бічні смуги з симетричними лінійчастими спектрами (рис. 1.6, б). Нарешті, при модуляції сигналу реальним випадковим сигналом смуги бічних частот будуть суцільними (рис 1.6, в).

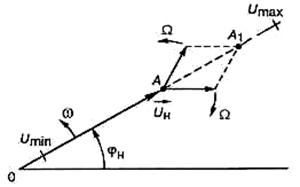
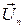Для більшого унаочнення амплітудно-модульований сигнал можна розглядати у вигляді векторної діаграми (рис. 1.7, а). На ній в полярній системі координат при довільній початковій фазі відкладають вектор , який відповідає амплітуді носійного коливання. Стрілка показує, що цей вектор обертається з кутовою швидкістю 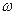навколо полюса. Менші вектори відповідають амплітудам бічних частот. На діаграмі показано, що відносно полюса вони обертаються з кутовими швидкостями 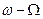і . Ці вектори для зручності додавання можна перенести паралельно з полюса системи до вершини вектора 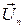(рис. 1.7, б). Тоді видно, що відносно цієї вершини вони обертаються з кутовими швидкостями та 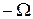. Отже, максимального значення сума цих трьох векторів набуває тоді, коли всі вектори збігаються за напрямком. Це відповідає точці 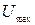на діаграмі. Відповідно мінімальне значення позначено точкою 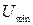і воно буде тоді, коли вектори бічних частот мають напрямок, протилежний вектору носійної частоти.

а

б

в

Рис. 1.6. Спектральне подання амплітудно-модульованого сигналу при тональній

модуляції (а), модуляції кількома сигналами повідомлення (б) і випадковими сигналами

повідомлення (в)

а

б

Рис. 1.7. Векторне подання амплітудно-модульованого сигналу.

Векторна діаграма показує принципову можливість появи такого спотворення сигналу, як паразитна ЧМ, що виникає в каналах зв'язку. Як випливає з діаграми чиста AM сигналу буде тільки за умови точної симетрії векторів, які відображають амплітуди бічних частот, коли вони утворюють ромб. Однак у реальних електричних колах ця симетрія може бути порушена, наприклад, через різне підсилення або згасання окремих складових спектра. Тоді кінець підсумкового вектора не буде переміщуватись по прямій між точкам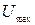и й 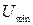, а спостерігатиметься деяке його коливання відносно вектора носійної частоти з деяким випередженням і відставанням від неї. Це рівнозначно тому, що підсумковий вектор коливатиметься з деякою частотою відносно положення вектора носійної частоти. Таке явище називається паразитною ЧМ і вкрай неприпустиме при передачі сигналу, оскільки висока стабільність частоти передавача є основною умовою надійності зв’язку.

Амплітудна модуляція — це не тільки найпростіший для вивчення, не тільки очевидний вид модуляції, а й найгірший з точки зору економічності і завадозахищеності. Справа в тому, що більшість природних і штучних завад (грозові розряди, теплові шуми, промислові джерела, сусідні радіостанції тощо) впливають саме на амплітуду сигналу. На передачу повідомлення при AM сигналу витрачається лише 5 % потужності джерела, що випромінює сигнал. Решта потужності переноситься сигналом носійної частоти, який ніякої інформаційної цінності не має. Тому для високоякісної і економічної передачі інформації використовують більш економічну і завадозахищену кутову модуляцію, хоча платою за ці її переваги є більш широка смуга частот, необхідна для передачі частотно-модульованого сигналу.

Кутова модуляція полягає в тому, що за законом сигналу повідомлення змінюється миттєве значення фазового кута, тобто повна фаза коливань :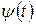

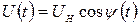, (1.14)

де .

Залежно від того, яка частина повної фази коливань (частота або фаза 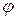) змінюється за законом сигналу повідомлення, кутова модуляція відповідно називається частотною (ЧМ) або фазовою (ФМ).

Нехай миттєва частота носійного коливання змінюється за законом

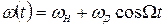, (1.15)

де 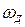— девіація частоти, що дорівнює максимальному відхиленню частоти від носійної частоти .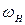

Тоді повна фаза частотно-модульованих коливань

, (1.16)

тобто частотно-модульоване коливання описується рівнянням

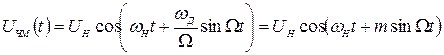, (1.17)

де 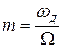— індекс кутової модуляції, що характеризує максимальне відхилення фази коливань.

Після тригонометричних перетворень (1.17) дістанемо

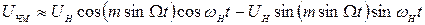(1.18)

Як бачимо, частотно-модульований сигнал складається з двох амплітудно-модульованих коливань і для знаходження його спектра слід визначити спектри функцій 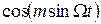та 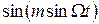. Проте ці функції нелінійні, тому просте перенесення спектра 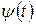на носійну частоту неможливе. В цьому разі доцільно розглянути два окремих випадки: з малим індексом кутової модуляції сигналу і великим його значенням .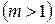

При маємо

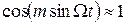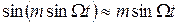; . (1.19)

3 урахуванням цих наближених значень функцій після тригонометричних перетворень (1.18) дістанемо

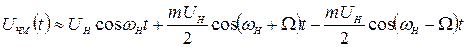(1.20)

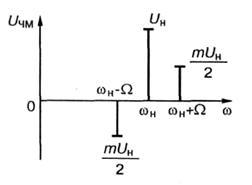
а б

Рис. 1.8. Векторне подання частотно-модульованого сигналу при малому індексі

модуляції

Цей вираз за зовнішнім виглядом з точністю до знака збігається з виразом (1.12). Це значить, що при малих 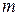спектр коливання з ЧМ відрізняється від спектра коливання з AM лише фазою для нижньої бічної частоти (рис.1.8, а). Якщо ж розглядати векторну діаграму (рис. 1.8, б), то видно, що зміна фази бічної частоти на протилежну приводить до того, що вектор носійного коливання з часом змінює свою фазу коливань.

Для аналізу спектрального складу сигналу при слід скористатися теорією бесселевих функцій і розвинути вирази (1.19) в ряди за цими функціями та здобути спектр, який містить нескінченну кількість бічних частот, симетричних відносно носійної. Амплітуди складових спектра пропорційні коефіцієнтам бесселевих функцій, тобто залежать від 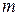і порядку функцій 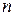. Аналіз показує, що при великих 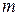значення коефіцієнтів бесселевих функцій за межами 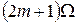різко прямують до нуля і тому можна обмежитися шириною спектра, близькою до повної смуги девіації, тобто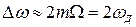

Отже, при кутовій модуляції якість переданого сигналу значно поліпшується саме завдяки розширенню спектрального складу сигналу; тому здійснити її можна тільки з надвисокочастотними носійними сигналами. Як випливає з векторної діаграми (див. рис. 1.8, б), тут виникає паразитна AM сигналу, вона не впливає на якість передачі інформації, оскільки легко усувається амплітудним обмеженням сигналу.

Читайте також:

1. Алфавітний підхід до вимірювання кількості інформації.
2. Аналіз зовнішньої інформації
3. Аналіз інформації та постановка задачі дослідження
4. Аналіз та інтерпретація інформації
5. Аналіз та компонування інформації для проекту
6. Аналіз та узагальнення отриманої інформації.
7. Аналіз якості виробничої інформації
8. Аналітико-синтетична переробка інформації
9. Аналітична обробка інформації вузлами інформаційно-аналітичної функціональної підсистеми МОЗ України і питань НС.
10. БАГАТОКАНАЛЬНІ СИСТЕМИ ПЕРЕДАЧІ ІНФОРМАЦІЇ
11. Бази даних як засіб зберігання й обробки інформації

Переглядів: 2146