
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Основні формули з розділу «Механіка»
Середня швидкість і середнє прискорення: 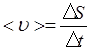 ;
; 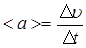 ,
,
де DS - шлях, пройдений точкою за інтервал часу Dt.
Шлях DS, на відміну від різниці координат, Dx = x2 – x1 не може приймати негативні значення, тобто DS³0.
Миттєва швидкість і миттєве прискорення при прямолінійному русі:
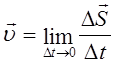 ,
, 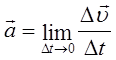 ,
,
де Д 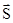 – вектор переміщення.
– вектор переміщення.
Якщо прискорення однакове в усіх точках шляху і в будь-який момент часу, то рух буде рівнозмінним.
Кінематичне рівняння рівномірного руху матеріальної точки вздовж осі Х:
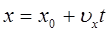 ,
,
де x0 – початкова координата.
При рівномірному русі  .
.
Кінематичне рівняння рівнозмінного руху матеріальної точки уздовж осі X:
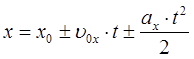 ,
,
де хо – початкова координата рухомої точки у момент часу t = 0;
 о – швидкість точки в даний момент часу;
о – швидкість точки в даний момент часу;
а – прискорення.
Швидкість і шлях рівнозмінного поступального руху:
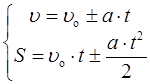 .
.
Швидкість і переміщення привільному падінні:
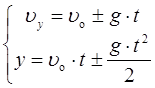 ,
,
де g – прискорення вільного падіння.
Кутова швидкість і кутове прискорення при обертальному русі:
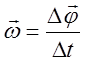 ;
; 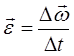 .
.
Кінематичне рівняння рівнозмінного обертального руху:
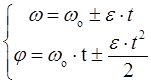
Зв'язок між лінійними і кутовими величинами при обертальному русі:
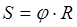 , S – довжина дуги, пройдена точкою, j – кут обертання точки, R – радіус обертання точки;
, S – довжина дуги, пройдена точкою, j – кут обертання точки, R – радіус обертання точки;
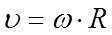 ;
; 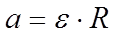 ;
; 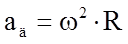 .
.
Імпульс (кількість руху) матеріальної точки масою m, що рухається зі швидкістю:
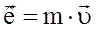 .
.
Основне рівняння динаміки поступального руху:
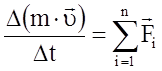 .
.
Сили, що розглядаються в механіці:
а) сила пружності:
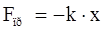 ,
,
де k – коефіцієнт пружності; x – абсолютна деформація.
Механічна напруга при пружній деформації тіла: 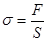 ,
,
де F - сила, що розтягує або стискає тіло; S - площа поперечного перерізу тіла.
Відносне поздовжнє розтягування (стиснення): 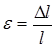 ,
,
де 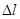 – зміна довжини тіла при розтягуванні (стисненні);
– зміна довжини тіла при розтягуванні (стисненні); 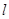 - довжина тіла до деформації.
- довжина тіла до деформації.
Закон Гука для поздовжнього розтягування (стиснення): 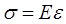 ,
,
де 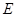 - модуль Юнга.
- модуль Юнга.
б) сила тертя ковзання:
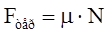 ,
,
де µ – коефіцієнт тертя; N – сила нормальної реакції опори.
в) сила гравітаційної взаємодії (сила тяжіння):
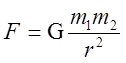 ,
,
де G – гравітаційна стала; m1 і m2 – маси взаємодіючих тіл; r – відстань між тілами (тіла розглядаються як матеріальні точки);
г) чисельне значення сили, що діє на тіло, яке рухається по дузі кола радіусом R:
 .
.
Закон збереження імпульсу (кількості руху) для замкненої (ізольованої) системи:
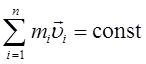 ,
,
або для двох тіл (i = 2):
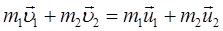 ,
,
де 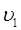 і
і  – швидкості тіл до взаємодії;
– швидкості тіл до взаємодії;
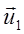 і
і 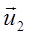 – швидкості тих же тіл після їх взаємодії.
– швидкості тих же тіл після їх взаємодії.
Кінетична енергія тіла:
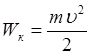 .
.
Потенціальна енергія:
а) пружно деформованого тіла:
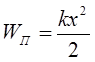 ,
,
де k – коефіцієнт пружності (жорсткість) тіла; x – абсолютна деформація;
б) тіла, піднятого над поверхнею Землі:
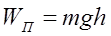 ,
,
де g – прискорення вільного падіння; h – висота тіла над рівнем, прийнятим за нульовий (формула справедлива за умови h<<RЗ, де RЗ – радіус Землі).
Закон збереження повної механічної енергії (для замкненої системи, де діють консервативні сили):
W = Wк+WП = const.
Робота А, здійснювана зовнішніми силами, визначається як міра зміни кінетичної енергії системи (тіла): A = DW = W2 - W1
Робота:
а) постійної сили F:
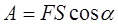 ,
,
де a - кут між напрямами сили 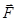 і переміщення
і переміщення 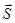 ;
;
б) пружної сили:
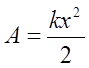 .
.
Потужність: 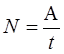 .
.
Момент сили відносно нерухомої осі обертання:
M = F d, де d=r∙sinα – плече сили F.
Кінематичне рівняння гармонійних коливань матеріальної точки:
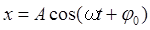 ,
,
де х – зсув точки, що коливається, від положення рівноваги;
А – амплітуда коливань;
w – кругова або циклічна частота;
j0 – початкова фаза коливань;
t – час.
Періодом коливань називається проміжок часу між двома послідовими максимальними відхиленнями фізичної системи від положення рівноваги.
Зв’язок між періодом коливань та циклічною частотою ω:
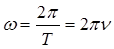 ,
,
де Т – період коливань точки; v – частота коливань.
Повна енергія точки, що коливається:
W = Wк+WП = 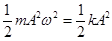 .
.
Період власних коливань:
а) математичного маятника
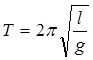 ,
,
де l – довжина маятника; g – прискорення вільного падіння;
б) пружинного маятника
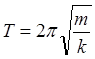
де m – маса тіла, що коливається; k – жорсткість пружини.
Довжина хвилі
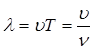 ,
,
де Т – період коливання;
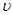 – швидкість розповсюдження хвилі;
– швидкість розповсюдження хвилі;
v – частота коливань.
Приклади розв`язування задач
ЗАДАЧА 1
Автомобіль першу половину шляху рухався зі швидкістю 72 км/год. Потім половину часу він рухався зі швидкістю 42 км/год, а іншу половину часу зі швидкістю 30 км/год. Визначити середню швидкість руху автомобіля.
Дано:
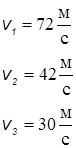
| Розв'язок: Середня швидкість руху:  . Загальний шлях . Загальний шлях 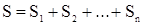 , або , або 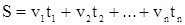 . За умовою задачі: . За умовою задачі: 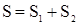 , або , або 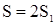 . Так як . Так як 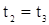 , то , то
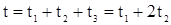 . Зі співвідношення . Зі співвідношення 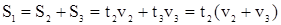 визначимо визначимо 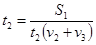 . .
|
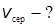
|
З урахуванням цього:
t = t1+ 2t2 = 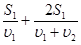
визначимо середню швидкість руху:
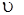 сер
сер 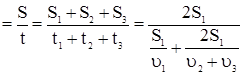
скоротимо чисельник і знаменник на S1 i будемо мати:
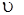 сер =
сер = 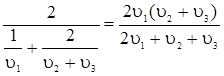
Обчислимо: 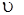 сер=
сер= 
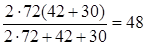 (км/год)
(км/год)
Вiдповiдь: 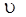 сер=48 км/год
сер=48 км/год
ЗАДАЧА 2
З яким прискоренням зісковзує тiло з похилої площини з кутом нахилу  , якщо з похилої площини з кутом нахилу
, якщо з похилої площини з кутом нахилу 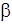 воно рухається вниз рiвномiрно?
воно рухається вниз рiвномiрно?
Дано: Розв'язок:
| < α < β |
| а - ? |
 На тiло дiють три сили: сила тяжiння
На тiло дiють три сили: сила тяжiння 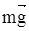 сила нормальної реакції опори
сила нормальної реакції опори  з боку похилої площини i сила тертя
з боку похилої площини i сила тертя 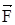 тер. Якщо по похилiй площинi з кутом нахилу
тер. Якщо по похилiй площинi з кутом нахилу 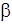 тiло рухається рiвномiрно , то прискорення а = 0 i вiдповiдно:
тiло рухається рiвномiрно , то прискорення а = 0 i вiдповiдно:
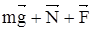 тер =0 (1)
тер =0 (1)
Виберемо дві взаємно перпендикулярні вісі координат OX та OY і запишемо рівняння (1) в проекціях на ці вісі:
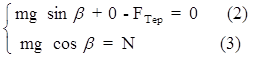
Так як сила тертя Fтер = 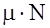 ,
,
де 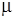 - коефіцієнт тертя ковзання, то: Fтер =
- коефіцієнт тертя ковзання, то: Fтер = 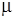 mg cos
mg cos 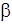 .
.
Підставимо значення Fтер в рівняння (2):
mg sin 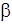 -
- 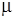 mg cos
mg cos 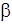 =0 (4)
=0 (4)
з рівняння (4) випливає, що 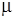 =tg
=tg 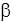 (5)
(5)
Пам'ятаємо, що коефіцієнт тертя залежить від матеріалу стикових поверхонь тіл і тому буде однаковим в першому і другому випадках.
Якщо тіло рухається з прискоренням по похилій площині з кутом нахилу 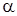 , то на підставі другого закону Ньютона:
, то на підставі другого закону Ньютона:
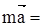
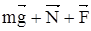 тер; (6)
тер; (6)
в проекціях на вісі координат:
ma=mg sin  - Fтер (7)
- Fтер (7)
0=mg cos  - N (8)
- N (8)
З рівняння (8) маємо: N=mg cos  ,
,
з урахуванням цього: Fтер = 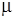 mg cos
mg cos  .
.
Підставимо значення 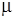 з (5):
з (5):
F =tg 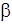 mg cos
mg cos  . З (7) будемо мати: ma=mg sin
. З (7) будемо мати: ma=mg sin  - tg
- tg 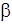 mg cos
mg cos  , або остаточно: a=g sin
, або остаточно: a=g sin  - gtg
- gtg 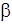 cos
cos  .
.
Відповідь: a=g (sin  - tg
- tg 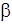 cos
cos  ).
).
ЗАДАЧА 3
Радіус малої планети 250 км, середня густина 
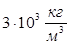 . Визначити прискорення вільного падіння на поверхні цієї планети.
. Визначити прискорення вільного падіння на поверхні цієї планети.
Дано: Розв'язок:
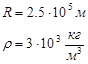
|
| gn -? |
За законом всесвітнього тяжіння на тіло масою m на цій планеті діє сила 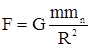 ,
,
де G - гравітаційна стала,
G= 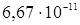
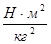 ; mn - маса планети;
; mn - маса планети;
R - радіус планети. Позначимо прискорення вільного падіння на цій планеті gn. Тоді: 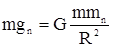 , або
, або 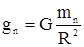 . Масу планети можна визначити за формулою:
. Масу планети можна визначити за формулою: 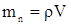 , де
, де 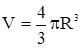 - об'єм планети.
- об'єм планети.
З урахуванням цього:  .
.
Обчислимо: 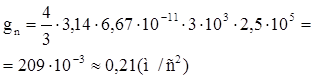
Відповідь: gn = 0,21 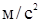 .
.
ЗАДАЧА 4
Снаряд масою m=5 кг, що вилетів з гармати, у верхній точці траєкторії має швидкість 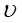 =300 м/с. У цій точці він розірвався на 2 осколки, причому більший осколок масою m1=3 кг рухається в зворотному напрямку зі швидкістю
=300 м/с. У цій точці він розірвався на 2 осколки, причому більший осколок масою m1=3 кг рухається в зворотному напрямку зі швидкістю 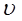 1=100 м/с. Визначити швидкість
1=100 м/с. Визначити швидкість 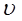 2 другого, меншого осколка.
2 другого, меншого осколка.
Дано: Розв'язок:
m=5 кг
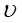 =300 м/с
m1=3 кг =300 м/с
m1=3 кг
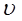 1=100 м/с 1=100 м/с
|
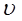 2- ? 2- ?
|
Запишемо закон збереження імпульсу для непружного удару в умовах даної задачі: m 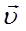 =m1
=m1 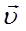 1+m2
1+m2 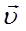 2
2
В скалярному вигляді: m 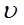 = –m1
= –m1 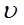 1+m2
1+m2 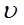 2. (1)
2. (1)
Масу другого осколка знайдемо за різницею мас снаряду та першого осколка: m2=m –m1. (2)
Підставимо (2) в (1): 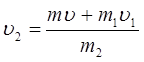 . Зробимо обчислення:
. Зробимо обчислення: 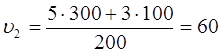 (м/с).
(м/с).
Відповідь: 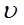 2=60 м/с.
2=60 м/с.
ЗАДАЧА 5
До нижнього кінця вертикального дроту завдовжки 5 м і площею поперечного перерізу 2 мм2 підвішено вантаж 5,1 кг, внаслідок чого дріт видовжився на 0,6 мм. Визначити модуль Юнга для матеріалу дроту.
Дано: Розв'язок:
 = 5 м
S = 2 мм
m = 5,1 кг = 5 м
S = 2 мм
m = 5,1 кг
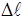 = 0,6 мм = = = 0,6 мм = = 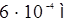
| Визначимо механічну напругу: 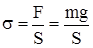 ;
визначимо відносне видовження дроту: ;
визначимо відносне видовження дроту: 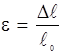 З формули
З формули 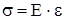 виразимо модуль Юнга Е: виразимо модуль Юнга Е:
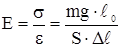 ;
Обчислимо: ;
Обчислимо: 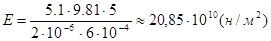 Відповідь:
Відповідь: 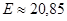 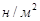
|
| Е - ? |
Читайте також:
- II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
- II. Основні засоби
- II.3. Основні способи і прийоми досягнення адекватності
- Адвокатура в Україні: основні завдання і функції
- Активи, що реалізуються повільно (А3) – це статті 2-го розділу активу балансу, які включають запаси та інші оборотні активи (рядки 100 до 140 включно, а також рядок 250).
- Амортизація основних засобів, основні методи амортизації
- Артеріальний пульс, основні параметри
- Банківська система та її основні функції
- Безпосереднє обчислення з використанням формули Ньютона-Лейбніца.
- Біржові товари і основні види товарних бірж. Принципи товарних бірж.
- Буддійська філософія і її основні школи
- Будова й основні елементи машини
| <== попередня сторінка | | | наступна сторінка ==> |
| Загальні рекомендації до розв’язання задач | | | Задачі для самостійного розв’язування з розділу «Механіка» |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |