• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Сучасні поняття про фігуру Землі та її зовнішнє гравітаційне поле

Розміри Землі і форма її поверхні як в цілому, так і окремих частин є предметом вивчення різних дисциплін (фізична геодезія або теорія фігури Землі, фізика Землі, теоретична геофізика тощо), в яких ці питання розглядаються з неоднакових позицій і різними методами, що обумовлено своїми специфічними задачами. Поняття “фігура Землі” є неоднозначним і має різне трактування в залежності від використання отримуваних даних.

З фізичної геодезії відомо, що потенціал сили ваги Землі 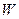визначається як сума потенціалу притягання Землі і потенціалу відцентрової сили . Відповідно, потенціал притяганняв теорії фігури Землі це є потенціал сили притягання одиничної маси в довільній точці простору 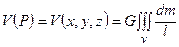всіма масами планети Земля, а потенціал відцентрової сили Землі – це потенціал сили, яка виникає під час обертання Землі навколо своєї осі і діє на одиничну масу на поверхні планети або в найближчому її околі . 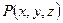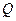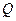У цих виразах: позначає точку, в якій обчислюється, – змінна точка всередині тіла Землі, яка приймає зміст центра мас елемента , - відстань між і (просторова пряма лінія), 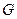– Ньютонова гравітаційна стала (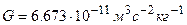), 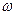- кутова швидкість обертання Землі. Отже,

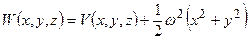. (6.1)

Якщо позначити силу ваги або прискорення сили ваги через 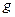і знати потенціал сили ваги 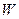даної точки, то можна обчислити складові сили ваги по осях координат

,

а, знаючи складові сили ваги легко можна визначити модуль вектора прискорення сили ваги

,

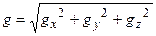та його напрям

.

Фізична поверхня Землі в межах континентальної частини з її відносними підвищеннями та пониженнями не є правильною математичною поверхнею і не може бути виражена яким-небудь математичним рівнянням. Звідси виникла задача встановлення поняття і вибору математичної поверхні Землі.

Оскільки фізична поверхня Землі складається переважно із поверхні морів та океанів (загальна площа материків складає приблизно лише четверту частину всієї поверхні Землі, а їх середня висота над рівнем Світового океану дорівнює тільки десятитисячній частині земного радіуса), то в свій час за математичну поверхню Землі умовно була прийнята поверхня Світового океану в стані рівноваги води.

Поверхня води Світового океану як рідка маса, що знаходиться тільки під дією сили земного притягання та відцентрової сили обертання Землі, є однією з рівневих поверхонь потенціала сили ваги. Ця поверхня характеризується тією основною властивістю, що на ній потенціал прискорення сили ваги всюди має одне і теж постійне значення, тобто в кожній її точці напрям нормалі до неї збігається з напрямом дії сили ваги або з прямовисною лінією. Якщо рівневу поверхню Світового океану продовжити під материками так, щоб вона всюди перетинала напрям прямовисної лінії під прямим кутом, то тоді отримається деяка замкнута поверхня, яка і буде характеризувати математичну фігуру Землі.

Вказана властивість будь-якої рівневої поверхні може бути виражена математичним рівнянням,

(6.1´)

в якому потенціал сили ваги є функцією від координат її поточної точки та розподілу маси всередині тіла, обмеженого заданою рівневою поверхнею. В такій редакції рівнева поверхня, яка збігається з поверхнею Світового океану в стані рівноваги і відповідним чином продовжена під материками, є математичною поверхнею. Проте вигляд або форма цієї поверхні залежать від розподілу сили ваги на ній або внутрішньої будови Землі.

Згодом остаточно вияснилося, що фігура Землі, утворена рівневою поверхнею, яка збігається з поверхнею Світового океану і відповідним чином продовжена під материками, має досить складну форму. Це пояснюється нерівномірним розподілом сили ваги на поверхні Землі і залежить від структури земної кори. Вказана математична поверхня не може бути представлена повністю якою-небудь правильною геометричною фігурою, що має просте математичне рівняння. Для математичної фігури Землі у вказаному її розумінні в 1873 р. був запропонований термін “геоїд”, який закріпився в геодезичній науці до сьогоднішнього часу.

Результати астрономо-геодезичних робіт підтвердили висновки про те, що вказана вище математична поверхня, хоч і відповідає фізичній природі Землі, проте може значно відрізнятися від правильної математичної фігури – загального земного сфероїда – фігури, яка найкращим чином представляє Землю як в гравітаційному так і в геометричному відношенні.

Отже, через те, що дійсне поле сили ваги є математично дуже складним, виділяють (в якості референцного) нормальне поле сили ваги простої аналітичної природи. В загальному, нормальний потенціал сили ваги 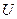вибирається так, що референц-еліпсоїд є еквіпотенціальною поверхнею для :

,

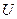а геоїд - еквіпотенціальною поверхнею дійсного потенціала сили ваги :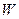

.

Відмінність потенціала сили ваги реальної Землі 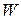від потенціала сили ваги Нормальної Землі 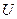носить назву збурюючого потенціала, тобто .

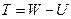Для обчислення нормальної сили ваги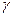на еліпсоїді служить замкнута формула Сомільяна

, (6.1´´)

де і 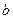- параметри еліпсоїда, і позначають нормальну силу ваги на екваторі і полюсі відповідно.

Отже, найбільш відомою узагальненою фігурою Землі є загальний земний сфероїд, точнішне рівневий еліпсоїд обертання, який ще називають Нормальна Земля. Під цим терміном розуміється узагальнена модель Землі як планети в цілому, яка з однієї сторони відтворює її основні властивості в усередненому вигляді, а з другої – найбільш просто представляє її для математичного опису.

Нормальна Земля при розв’язуванні наукових і практичних задач виконує двояку роль: вона застосовується або як правдоподібна модель Землі, яка з достатньою точністю замінює реальну Землю (в астрономії, геофізиці, картографії, навігації тощо), або там, де вимагається більш висока точність, як досить добре її перше наближення ( в геодезії, гравіметрії, космічній геодезії тощо).

Чисто теоретично при вивченні фігури Землі у відношенні її виду та розмірів можна було би розглядати будь-яку із її рівневих поверхонь, оскільки від одної із них можна теоретично перейти до іншої рівневої поверхні. Для переходу від даної або вихідної рівневої поверхні до другої нескінченно близької до неї рівневої поверхні 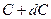, розташованої на висоті , можна було би застосувати наступну формулу

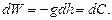(6.2)

Але для переходу від одної рівневої поверхні до другої, як показує формула (6.2), необхідно знати закон зміни сили ваги 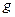з висотою. Оскільки закон зміни сили ваги з висотою всередині земної маси точно не відомий, то теоретична можливість переходу від одної рівневої поверхні до другої рівневої поверхні Землі не може бути здійснена строго у практичному відношенні.

Вибір і вивчення довільної рівневої поверхні для того, щоб потім визначати відносно неї елементи конкретно заданої рівневої поверхні теж не може бути абсолютно умовним. Для геодезії особливе значення має вивчення вигляду і розмірів безпосередньо тієї рівневої поверхні, яка проходить близько до фізичної поверхні Землі та найкращим чином характеризує її дійсну фігуру. Зрозуміло, що вона має бути вибрана у повній відповідності до будови і характеру зовнішньої поверхні Землі як планети в цілому. Це означає, що нормальний потенціал 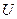необхідно встановити так, щоб збурюючий потенціал 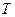був гармонійною функцією з високою точністю наближення.

6.2. Визначення відступів геоїда (квазігеоїда)

Відступи геоїда над земним еліпсоїдом – це перевищення точок геоїда відносно поверхні еліпсоїда. Виміряти безпосередньо ці перевищення не можна. Лише відхилення прямовисних ліній 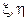та аномалії сили ваги 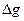є тими безпосередньо виміряними величинами, які служать для вивчення фігури Землі. Фігура Землі представляється у вигляді земного еліпсоїда, а однією із задач її вивчення і є визначення відступів фігури геоїда від поверхні еліпсоїда.

Для визначення відступів геоїда (квазігеоїда) чисто гравіметричним методом з використанням лише аномалій сили ваги, відомих по всій поверхні Землі, можна скористатися теорією та відповідними формулами Стокса (теорією та формулами Молоденського). Розглянемо коротко ці підходи.

Проблема визначення зовнішнього гравітаційного поля W Землі і форми рівневої поверхні S потенціалу сили ваги за її значеннями на цій поверхні, згідно (6.2)

,

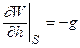вперше поставлена і розв’язана англійським вченим Стоксом.

Стокс звів цю проблему до одного з видів крайових задач теорії потенціалу (потенціали в ділянках, де немає притягувальних мас, є гармонійними функціями). Замість W шукається збурюючий потенціал 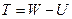. Розв’язок Стокса визначає тільки головну частину Т. Поскільки вимірювання g виконують на фізичній поверхні S, а не на рівневій поверхні (геоїді) S, то потрібно ще перейти із S до S (задача редукування), попередньо “забравши” маси, що лежать між S і S (задача регуляризації геоїда). Обидві ці задачі не розв’язуються однозначно через те, що не відома густина мас між S і S. Тому розв’язок Стокса є наближеним розв’язком задачі визначення форми геоїда - це так зване стоксове наближення [11]. Її строгий розв’язок вимагає регуляризації геоїда і редукування виміряних g на геоїд, що неможливо точно здійснити в принципі. Узагальненням теорії Стокса, із якої виключена необхідність регуляризації геоїда і редукування виміряних g, є теорія Молоденського. Щоб уникнути гіпотез і припущень, потрібно вважати потенціал та його похідні заданими тільки в тих місцях, в яких вони безпосередньо вимірюються, тобто на фізичній поверхні Землі. Крайова умова повинна бути задана також на фізичній поверхні Землі, тобто потрібно відмовитися від вивчення рівневої поверхні – геоїда, а перейти до вивчення нерівневої або кусково-рівневої поверхні. В цьому випадку можна побудувати гравітаційне поле в усьому зовнішньому просторі і вивчати форму поверхні, поза якою немає маси, що притягує, тобто фізичної поверхні Землі. Така постановка проблеми та її розв’язок належить М.Молоденському (40-60 р.р. ХХ ст.). В свої роботах він показав, що форма фізичної поверхні Землі і потенціал поза нею, можуть бути визначені, якщо мати в розпоряджені тільки дані спостережень на поверхні Землі, не застосовуючи при цьому модельні представлення внутрішньої будови Землі, переважно земної кори. Таку задачу стали називати задачею Молоденського. Дана задача буде полягати перш за все в тому, щоб отримати рівняння, яке пов’язує фігуру дійсної Землі з такими функціями, числові значення яких отримуються із астрономо-геодезичних та гравіметричних вимірювань на цій поверхні.

При вивченні фігури фізичної поверхні Землі так само, як і при вивченні рівневої фігури Землі методом Стокса, вводиться допоміжна (проміжна відлікова) поверхня – квазігеоїд. Відстань між точками квазігеоїда і еліпсоїдом називають висотою квазігеоїда або аномалією висоти. До її визначення і зводиться, в основному, задача визначення фізичної поверхні Землі або задача Молоденського .

Історично так склалося, що через недостатньо повну гравіметричну вивченність земної поверхні в цілому визначення відступів геоїда від поверхні прийнятого еліпсоїда вивчалося геометричними методами. Роль гравіметричних даних зводилася до їх використання при інтерполюванні тих чи інших величин. Оскільки такі класичні методи не втратили свого значення і в теперішній час, то розглянемо їх суть.

Читайте також:

1. II. Поняття соціального процесу.
2. V. Поняття та ознаки (характеристики) злочинності
3. А/. Поняття про судовий процес.
4. Адміністративний проступок: поняття, ознаки, види.
5. Адміністративні провадження: поняття, класифікація, стадії
6. Акти застосування юридичних норм: поняття, ознаки, види.
7. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
8. Антропогенний вплив на природне середовище та сучасні екологічні проблеми
9. АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ
10. Аудиторські докази: поняття та процедури отримання
11. Багатозначність слів у сучасній українській мові
12. Базове поняття земле оціночної діяльності.

Переглядів: 3818