
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
БАНКІВСЬКІ ОПЕРАЦІЇ
Це найпростіший і часто використовуваний метод. Він дозволяє розрахувати період, протягом якого проект окупиться. Якщо цей термін виявиться прийнятним для інвестора, то проект може бути прийнятим. Процедура методу полягає у складанні грошового потоку проекту за роками та визначенні періоду окупності — часу протягом якого сума грошей, затрачена на проект, буде відшкодована. Розглянемо проект з наступним грошовим потоком:
| Рік | Горошовий потік (дол. США) |
| -4,000 (витрати) | |
| +1,000 | |
| +1,000 | |
| +2,000 (період окупності) | |
| +3,000 | |
| +1,000 |
Як видно, даний проект має трьохрічний період окупності.
Моделі оцінювання дохідності використаного капіталу.Даний метод полягає у визначенні відношення доходу, одержаного від реалізації проекту, до затрат, що вимагаються. Дохід обчислюється після відрахувань на амортизацію та до податкових відрахувань. До затрат належать початкова вартість проекту і робочий капітал (наприклад, сировина, затрати на склад готової продукції та ін.). У зарубіжній літературі зустрічається багато назв цього методу. Часто використовується абревіатура ROCE (return on capital employed).
Існує два способи вираження ROCE. Перший — це визначення відношення середньорічного доходу, одержаного за весь період здійснення проекту, до середньої вартості використаного капіталу. Другий — визначення відношення середньорічного доходу до вартості вкладеного капіталу. Нижче подано приклад, де використані обидва підходи.
Нехай компанія А збирається вкласти кошти в інвестиційний проект з початковими затратами капіталу 10000 дол. США і робочим капіталом 3000 дол. США. Проект буде здійснюватися чотири роки, його залишкова вартість складе 2000 дол. США. Грошовий потік подано нижче.
| Рік | Грошовий потік (дол. США) |
| +4,000 | |
| +6,000 | |
| +3,500 | |
| +1,500 |
За умови, що компанія застосовує метод рівномірного списання основного капіталу, дохід може обчислюватися як грошовий потік мінус амортизація. Щорічні відрахування на амортизацію складають:
($10000–$2000)/4=$2000. Щорічний потік доходу буде таким:
| Рік | Грошовий потік — амортизація (дол. США) | Дохід |
| 4,000-2,000= | 2,000 | |
| 6,000-2,000= | 4,000 | |
| 3,500-2,000= | 1,500 | |
| 1,500-2,000= | -500 | |
| Всього | 7,000 |
Середній щорічний дохід: $7000/4=$1750.
Початковий затрачений капітал складає $13000 (початкова вартість плюс робочий капітал). Середня вартість затраченого капіталу обчислюється: (початковий капітал — залишкова вартість)/2+залишкова вартість+робочий капітал. Тобто: ($10000–$2000)/2+$2000+$3000=$9000. Отже, дохідність на вкладений капітал становить $1750/$1300=0,135 або 13,5%, а дохідність на середню вартість використаного капіталу — $1750/$9000=0,194 або 19,4%.
Модель оцінювання інвестиційних проектів на основі сучасної вартості потоку платежів (модель NPV)
Платежі інвестиційного проекту, як правило, визначаються через певні рівні проміжки часу, наприклад, щотижня, щомісячно або щорічно. Надалі ми будемо грунтуватися на щорічному базисі. Платежі можуть бути позитивними (якщо є прибуток), негативними (якщо кошти, вкладені в проект, не перекриваються доходами) або нульовими.
Сучасна вартість потоку платежів визначається додаванням всіх сучасних вартостей платежів протягом розглядуваного періоду. Якщо А — певний платіж, що очікується через n років, то його сучасна вартість (PV — Present Value) дорівнює А/(1+r)n, де r — норма прибутку, а А/(1+r)n — це так званий коефіцієнт дисконтування. Далі ми докладніше розглянемо поняття норми прибутку. Поки що будемо вважати, що це дохідність безризикового активу, наприклад, державних облігацій.
Якщо ми розглядаємо проміжок часу n років і певний інвестиційний проект, то сучасна вартість його потоку платежів (NPV — Net Present Value) дорівнює:
NPV =  . .
| (5.1) |
Для прийняття рішення про вкладення коштів у проект керуються таким правилом:
1) якщо NPV³0, проект повинен виконуватися;
2) якщо NPV<0, від проекту відмовляються.
Наведемо приклад. Нехай безризикова дохідність державних облігацій складає 8%. Тоді матимемо.
| Рік | Грошовий потік (дол. США) | Коефіцієнт дисконтування | PV (дол. США) |
| 1,000 | · (1+0,08)0 | -1,000 | |
| · (1+0,08)-1 | +92.59 | ||
| · (1+0,08)-2 | +171.46 | ||
| · (1+0,08)-3 | +158.76 | ||
| · (1+0,08)-4 | +404.25 | ||
| NPV | -172/94 |
Так як NPV негативний, від цього проекту потрібно відмовитися.
Модель оцінювання інвестиційних проектів на основі внутрішнього коефіцієнта дохідності
В моделі NPV проект має позитивний NPV у тому випадку, коли дохід від проекту виражений у % буде вищим коефіцієнта дисконтування. NPV негативний, коли дохід нижчий коефіцієнта дисконтування, NPV рівний нулю, коли дохід дорівнюватиме коефіцієнтові.
Внутрішній коефіцієнт дохідності (IRR — Internal rate of ruturn) визначається як коефіцієнт дисконтування, за якого NPV проекту рівняється нулю. IRR це значення r, яке задовольняє рівняння:  =0. В простих випадках, таких як розглядуваний нижче проект, IRR визначається дуже просто.
=0. В простих випадках, таких як розглядуваний нижче проект, IRR визначається дуже просто.
| Рік | Грошовий потік |
| -$200 | |
| +$218 |
IRR проекту дорівнює r в рівнянні
-200+ 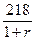 =0
=0
IRR = r = 0.09 або 9%.
Отже, коли б потоки платежів даного проекту дисконтувалися під 9%, вони мали б нульовий NPV:
| Рік | Потік платежів | Коефіцієнт дисконтування | PV | ||
| -$200 | (1 + 0.09)0 | -$200 | |||
| +$218 | (1 + 0.09)-1 | +$200 | |||
| NPV = | $0 | ||||
Розглянемо складніший приклад проекту, котрий має три часових періоди:
| Рік | Потікплатежів |
| -$100 | |
| +$60 | |
| +$55 |
IRR = r в рівнянні
-100+ 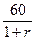 +
+ 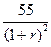 =0. Помножимо обидві частини рівняння на (1+r)2, і одержимо:
=0. Помножимо обидві частини рівняння на (1+r)2, і одержимо:
-100(1+r)2+60(1+r)+55=0. Розв’язком рівняння є:
(1+ r)=+1.10 або (1+r)=-0.50
Другий результат можна не брати до уваги, як такий, що не має смислу. Отже, r=0,10 або 10%.
Для знаходження IRR проектів із ще більшими періодами потоків платежів необхідно розв’язувати складні поліномінальні рівняння. Існує багато комп’ютерних програм, які розв’язують цю задачу. Хорошу апроксимацію розв’язання можна також одержати за допомогою математичної процедури, що називається лінійною інтерполяцією.
При застосуванні цього методу використовують пару коефіцієнтів дисконтування. Якщо NPV1 — це NPV з меншим коефіцієнтом, NPV2 — з більшим, а R1 і R2 — менший і більший коефіцієнти відповідно, то
IRR = Rl + 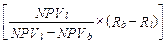
| (5.2) |
Розглянемо приклад проекту, потік платежів якого подано нижче:
| Рік | Потік платежів, дол. США |
| -10,000 | |
| +5,000 | |
| +8,000 | |
| +3,000 |
Використовуючи коефіцієнти дисконтування 4% і 20%, одержимо такі NPV:
з 4%, NPV1=+$4,871
з 20%, NPVr=+$1,458
IRR оцінюється так:
IRR = 4%+ 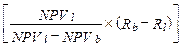 = 26,8%
= 26,8%
Для оцінювання інвестиційних проектів за допомогою моделі IRR слід вибирати проекти з найвищим IRR і відмовлятися від проектів з IRR меншим, ніж ринкова норма прибутку для безризикових активів.
Розглянемо тепер такий приклад.
Нехай компанія розглядає вкладення коштів у шість проектів і має для цього лише 215000 дол. США. Ринкова норма прибутку 10%. Будь-який проект може бути прийнятий або не прийнятий як повністю, так і частково (тобто компанія може здійснити деяку частину проекту). Компанія повинна максимізувати сучасну вартість загального грошового потоку з усіх проектів. Дані проектів подані в таблиці:
| Проекти | ||||||
| Рік | ||||||
| -25000 | -60000 | -90000 | -100000 | -120000 | -35000 | |
| NPV | ||||||
| IRR | 15.2 | 14.1 | 12.1 | 11.6 | 16.3 | 14.3 |
Як видно з таблиці, всі проекти могли б бути прийнятими, якщо б не існувало обмежень на суму початкових вкладів. Які проекти повинні здійснюватися за даних обмежень?
Спочатку розглянемо таку процедуру. Всі проекти розташовуються вряд за порядком зменшення NPV. Після цього послідовно приймаються проекти, доки вистачає коштів. Наступна таблиця демонструє це метод:
| Проект | NPV | Вкладені кошти | Сума вкладених коштів |
| 7/18 від 3-го проекту | |||
| Повний NPV |
Отже, ми одержали сучасну вартість $215000 шляхом вибору п’ятого, другого проектів, а також 38,89% від третього.
Тепер розглянемо вибір проектів, який грунтується на ранжуванні цих проектів за порядком зменшення дохідності:
| Проект | Дохідність | NPV | Вкладені кошти | Сума вкладених коштів |
| 16.3 | ||||
| 15.2 | ||||
| 14.3 | ||||
| 7/12 від 2-го проекту | 4.1 | |||
| 12.1 | ||||
| 11.6 | ||||
| Повний NPV |
Ми одержали повні NPV більшим, ніж за попереднім способом вибору проектів. Але звідси не витікає, що останній спосіб сам по собі кращий. Можна навести багато прикладів, в яких NPV буде більший відносно першого способу. Жоден з наведених способів не дозволяє одержати найбільшого за даних умов NPV.
Процедура, що дозволяє одержати найбільший NPV, базується на розташуванні проектів по зменшенню відношення NPV до початкових затрат (або відношення доходу до витрат). Застосування такого методу показано в наступній таблиці:
| Проект | Коефіцієнт | NPV | Вкладені кошти | Сума вкладених коштів |
| 0.137 | ||||
| 0.106 | ||||
| 0.085 | ||||
| 1/9 від 3-го проекту | 0.053 | |||
| 0.039 | ||||
| 0.028 | ||||
| Повний NPV |
За цією методикою вдалося одержати NPV, що на 9,7% більший, ніж при ранжуванні за дохідністю і на 11,5% більший, ніж при ранжуванні за NPV. Оптимальна група проектів дає такий грошовий потік:
| t = 0 | t = 1 | t = 2 |
| -215000 |
дохідність її трохи більша 15%.
Припустимо тепер, що є можливість виконувати одні й ті самі проекти по кілька разів. В наступній таблиці наведено приклад багаторазового використання проекту № 1:
| Проект | Коефіцієнт | NPV | Вкладені кошти | Сума вкладених коштів |
| 0.137 | ||||
| 0.137 | ||||
| 0.137 | ||||
| 0.137 | ||||
| 0.137 | ||||
| 0.137 | ||||
| 0.137 | ||||
| 3/5 від 1-го проекту | 0.137 | |||
| Повний NPV |
Повний NPV $29507 було досягнуто при інвестуванні 8,6 проектів № 1; це перебільшує на 44.2% максимум, який досягається при неможливості багаторазового інвестування в одні й ті самі проекти.
Якщо проект № 1 не може використатися більше одного разу, а в проект № 2 можна інвестувати багаторазово, то ми одержимо такі результати:
| Проект | Коефіцієнт | NPV | Вкладені кошти | Сума вкладених коштів |
| 0.137 | ||||
| 0.106 | ||||
| 0.106 | ||||
| 0.106 | ||||
| 1/6 від 2-го проекту | 0.106 | |||
| Повний NPV |
Отже, неможливість повторення проекту № 1 дала втрату $6002 в NPV.
Використання методу ранжування відносно доходу до витрат можна зобразити графічно. На рис. 5.5 показано рівні повних NPV, які досягаються за певних доступних початкових вкладень коштів. Коефіцієнти дохід-витрати рівні нахилам відрізків сегментів графіка NPV.
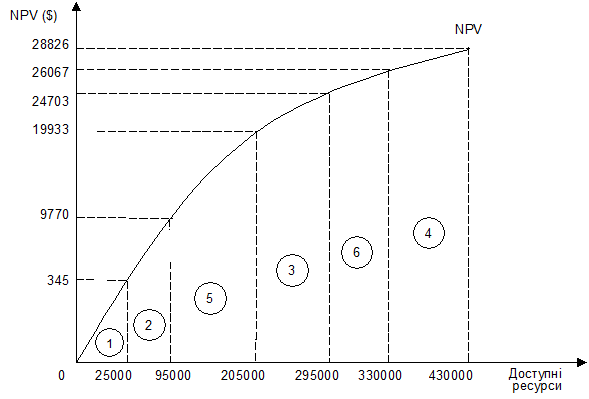
Рис. 5-5. Досягаємий NPV залежно від доступних ресурсів
Як видно з графіка, зі збільшенням доступних ресурсів зменшується коефіцієнт зростання NPV на затрачений долар. Так продовжується до останнього можливого проекту № 4. Отже, зі зняттям обмежень на вкладення коштів у проекти, можна досягнути максимального NPV у $28826 (за умови, що проекти не повторяться). Для цього необхідно $430000 початкових витрат.
Розглянемо проблему вкладення коштів при існуванні кількох обмежень на вибір проектів. Нехай на фондовому ринку присутні вісім компаній, які належать до чотирьох галузей (по дві на галузь). В наступній таблиці подано дохідність кожної компанії:
| Інвестиційний фонд | Хімічна промисловість | Торгівля | Переробна промисловість | |||||
| № компанії | ||||||||
| Дохідність, % | 4.8 | 5.4 | 7.5 | 8.5 |
Вважається, що інвестиційна політика компанії є збалансованою, якщо хоча б 30% її портфеля цінних паперів належать інвестиційним фондам, не більше 25% — переробним компаніям, хоча б 10% — хімічним, але не більше 20% — одній компанії будь-якої галузі. Необхідно знайти розв’язання, яке максимізувало б дохідність з урахуванням вищеназваних обмежень.
Така задача розв’язується методом лінійного програмування. Спочатку умову задачі формулюють у термінах лінійного програмування. Нехай xjє відсотком портфеля, який інвестується в акції j-ї компанії. Дохідність всього портфеля є середньозваженою сумою його частин. Необхідно максимізувати цю суму. Задача формулюється так:
Максимізувати
F = 4.8x1 + 5.4x2 + 7.5x3 + 8.5x4 + 9x5 + 10x6 + 15x7 + 18x8
за умови, що
x1 + x2+ x3 + x4+ x5+ x6 + x7 + x8 = 100
x1 + x2 ³ 30
x7 + x8 £ 25
x3 + x4 ³ 10
x1 £ 20
x2 £ 20
x3 £ 20
x4 £ 20
x5 £ 20
x6 £ 20
x7 £ 20
x8 £ 20
і де x1,x2, x3, x4, x5, x6, x7, x8 ³ 0
Відмітимо, що існує багато комп’ютерних програм, які розв’язують подібні задачі. Не заглиблюючись у питання лінійного програмування, подамо розв’язання:
x1 = 10 x2 = 20 x3 = 0 x4 =10 x5 = 15 x6 = 20 x7 = 5 x8 = 20
Дохідність даного портфеля 10,11%.
Очікувана сучасна вартість потоку платежів
У вищеописаних моделях передбачалося, що нам відомі точні потоки платежів тих чи інших проектів. Однак, насправді ми можемо визначити їх лише з певною ймовірністю. Це пов’язано з безліччю факторів, що впливають на здійснення інвестиційних проектів (наприклад, фактор циклу ділової активності). Одним з найпростіших методів оцінення проектів є метод визначення очікуваної сучасної вартості потоку платежів або ENPV, що рівняється середньому значенню сучасних вартостей потоків платежів проекту, визначених на підставі оцінок їх імовірності. Розглянемо приклад.
Нехай якась компанія розглядає можливість купівлі обладнання для виробництва цементу. Це обладнання коштує $1000 і очікується, що воно має термін використання три роки. Оцінювання щорічного доходу не можна визначити точно, тому що дохід залежить від стану будівельної галузі. Передбачається, що галузь може мати ажіотажне піднесення, нормальний стан, та стан занепаду. Компанія має таку статистику:
| Стан галузі | Рік | ||||
| (I) | Піднесення | -1000 | +500 | +700 | +980 |
| (II) | Нормальний | -1000 | +500 | +600 | +700 |
| (III) | Спад | -1000 | +300 | +300 | +250 |
Для оцінювання проектів компанія використовує коефіцієнт дисконтування 10%. За ним NPV проектів складає:
| Стан | NPV |
| I | +769 |
| II | +477 |
| III | -291 |
За оцінюванням певної незалежної організації, що прогнозує розвиток будівельної індустрії, ймовірності розглядуваних трьох станів цієї галузі такі:
| Стан | Ймовірність |
| I | 0.20 |
| II | 0.60 |
| III | 0.20 |
Очікуване значення NPV цього проекту обчислюється так:
| Стан | Ймовірність | NPV | Можливий NPV |
| I | 0.20 ´ | +769 = | +153.8 |
| II | 0.60 ´ | +477 = | +286.2 |
| III | 0.20 ´ | -291 = | -52.2 |
| +387.8 ENPV |
Так як проект має позитивний очікуваний NPV (ENPV), він може прийнятися компанією.
Аналіз чутливості
Аналіз реального інвестиційного проекту базується на врахуванні багатьох оцінок (початкових витрат, необхідних для виконання проекту, тривалості його здійснення, щорічних потоків платежів, залишкової вартості, а також коефіцієнт дисконтування для обчислення сучасної вартості потоку платежів). Оцінювання може бути зроблено для всіх цих факторів, потім проект аналізується за допомогою ENPV.
Для запобігання фінансових втрат необхідно знати, наскільки пропоноване рішення про вкладення коштів чутливе до помилок оцінювання факторів. Іншими словами, необхідно з’ясувати можливу граничну помилку оцінювання.
Рішення про вкладення або не вкладення коштів в певний проект приймається залежно від того, вище чи нижче нуля знаходиться його значення NPV. Отже, нуль є точкою повороту (рішення в ній змінюється на протилежне).
Аналіз чутливості — це метод визначення того, на яку величину має змінитися оцінений фактор проекту (за умови, що решта факторів не змінюються), щоб позитивний NPV зменшився до нуля. Отже, якщо фактор зміниться на більшу величину, ніж одержана в результаті аналізу чутливості, то початкове оцінювання проекту як прийнятного стане помилковим. Приклад використання цього методу подано нижче.
Допустимо, що є такі оцінки параметрів якогось інвестиційного проекту:
Початкові витрати: $1000
Термін виконання: 3 роки
Щорічний дохід: $2000
Щорічні витрати: $1500
Коефіцієнт дисконтування: 10%
На підставі цих оцінок визначимо NPV проекту:
| Рік | ||||
| Початкові витрати | -$1000 | |||
| Дохід | +$2000 | +$2000 | +$2000 | |
| Щорічні витрати | -$1000 | -$1500 | -$1500 | -$1500 |
| NPV | -$1000 | +$500 | +$500 | +$500 |
Дисконтуючи NPV грошових потоків при 10%, одержимо очікуваний NPV проекту, ENPV = -1000 + 500A3Ø0.10 = +$243 (A3Ø0.10 — стандартне позначення сучасної вартості постійного потоку платежів в один долар щорічно з коефіцієнтом дисконтування 10% і трьохрічному періоді,
AnØr = 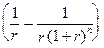 . .
| (8.3) |
Тепер послідовно знайдемо відхилення кожного з факторів на таку величину, за якої ENPV зменшується до нуля (залишаючи всі інші фактори постійними).
Початкові витрати:
Позначимо ці витрати символом x, тоді -х+A3Ø0.10 500=0, звідки х=1243. Отже, витрати можуть бути не більшими $1243. Після їх переходу за це значення рішення про інвестування в цей проект (тобто позитивний ENPV) буде помилковим. Іншими словами, початкове оцінювання може вирости на $243 або на 24,3%.
Термін виконання:
Позначимо його за x років, тоді:
1000+AхØ0.10 500=0. Знайдемо x, використовуючи лінійну інтерполяцію. Ми знаємо, що при х=3NPV=+$243, при х=2NPV=-1000+A2Ø0.10 500=-132. Отже, x зменшує NPV до нуля між 2 і 3 роками:
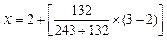 = 2.35
= 2.35
Тобто, якщо тривалість виконання проекту зменшиться на 0,65 року або на 21,7%, то початкове оцінювання інвестицій буде неправильним.
Доходи:
Нехай щорічний дохід буде x, тоді
-1000+х A3Ø0.10–1500 A3Ø0.10=0
х=(1000+1500 A3Ø0.10)/A3Ø0.10=-$1902
Отже, початкове оцінювання може зменшитися на $98 на рік або на 4,9%.
Щорічні витрати
Нехай вони будуть x, тоді
-1000+2000 A3Ø0.10 — хA3Ø0.10 = 0
х = (1000 + 2000 A3Ø0.10)/A3Ø0.10 = -$1598
Рішення про прийняття даного проекту буде коректним, коли щорічні витрати збільшаться порівняно з початково оціненими витратами не більше ніж на $98 на рік або на 6,5%.
Коефіцієнт дисконтування:
Позначимо його як x, тоді
-1000 + 500 A3Øх = 0
A3Øх = 1000/500 = 2.0
Використовуючи лінійну інтерполяцію при A3Ø0.20 = 2.11 та A3Ø0.25 = =1.95, знаходимо:
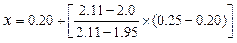 = 0.234
= 0.234
Отже, початково оцінений коефіцієнт можна збільшити на 13,4%.
Наведемо загальний результат аналізу:
| Фактор | Таблиця чутливості | |||
| Початкова оцінка | Максимальне значення | Максимальна зміна | Відсоток зміни | |
| Початкові витрати | +243 | +24.3% | ||
| Термін виконання | 2.35 | -0.65 | -21.7% | |
| Щорічний дохід | -98 | -4.9% | ||
| Щорічні витрати | +98 | +6.5% | ||
| Коефіцієнт дисконтування | 10% | 23.4% | +13.4% | +134% |
Моделі інвестиційної діяльності в умовах невизначеності
Основою ризику або невизначеності є наше незнання того, які з різних можливих подій дійсно відбудуться. Наприклад, якою буде ціна продажу блоку акцій через рік.
З поняттям ризику ми вже стикалися під час аналізу оцінюваних факторів, які впливають на прийняття рішення про вкладення коштів. Тепер розглянемо ризик докладніше.
Ризик, який ми будемо розглядати, є ризиком неотримання доходів, на котрі ми очікуємо від інвестиційного портфеля або проекту. Невизначеність доходу інвестиційного портфеля є наслідком невизначеності доходів активів, які складають його. Ці активи можуть мати один або кілька ризиків, що класифікуються за чотирма основними категоріями — кредитний ризик, ризик доходів, ринковий ризик та інфляційний.
Кредитний ризик. Кредитний ризик — це ризик зменшення або втрати очікуваних доходів, викликаний невиконанням позичальниками зобов’язань по кредиту. При цьому позичальники можуть взагалі відмовитися платити, чи заплатити лише частину або виплатити пізніше обіцяного. Позичальники можуть бути не готовими до виплати або не здатними зробити це через якісь несподівані обставини. В будь-якому випадку кредитор буде мати менший дохід, ніж спочатку обіцяний позичальником.
Ризик доходу. Для багатьох активів характерна зміна доходу, пов’язана зі специфікою активів. Так наприклад, дивіденди, одержані інвестором, можуть змінюватися час від часу в широких межах через дивідендну політику емітента. Ризиком доходу називається допустиме зменшення виплат доходу з активу.
Ринковий ризик. Доходи з багатьох активів (акції, нерухомість, іноземна валюта та ін.) відображають різницю між справжньою ціною активів та майбутньою ціною їх перепродажу. Ринковим ризиком називається зменшення або втрата доходів внаслідок зміни майбутньої ринкової ціни активу. Одним з важливих ринкових ризиків є ризик зміни валютного курсу.
Інфляційний ризик. Всі реальні доходи зазнають інфляційного ризику. Реальний дохід визначається як номінальний дохід мінус очікуваний відсоток інфляції. Зменшення або втрата очікуваних реальних доходів, викликаних змінами в очікуваній інфляції, називається інфляційним ризиком.
Модель очікуваної корисності
Інвестиційний менеджмент, як правило, здійснюється від імені численних інвесторів, які своїми рішеннями впливають на діяльність компаній в усьому світі. Тому для успішного аналізу інвестицій необхідно мати модель, що адекватно відображає відношення інвесторів до ризику: як вони сприймають його і як реагують на його присутність.
Перш за все, будемо передбачати, що власники акцій або інвестори діють раціонально й логічно. Точніше, можна сформулювати чотири основні аксіоми поведінки інвесторів у прийнятті рішень:
· інвестори можуть вибирати між альтернативами (інвестиційними проектами) через ранжування їх в певному порядку на свій розсуд;
· кожне таке ранжування є транзитивним, тобто, якщо альтернатива А краща за Б і альтернатива Б краща за С, то альтернатива А краща за С;
· інвестори не розрізняють альтернативи, які мають однаковий ризик;
· інвестори мають можливість зіставити з будь-якою інвестицією (з невизначеним доходом) її еквівалент, що має безризиковий дохід.
Пояснимо останню аксіому на прикладі. Допустимо, що інвестор має можливість вкласти кошти в проект, який з імовірністю 60% дасть йому $5000, а з імовірністю 40% — лише $1000. Згідно з останньою аксіомою інвестор може мати можливість вкласти кошти в актив, котрий дасть йому $3000 доходу без всяких умов. Отже, $3000 — це безризиковий еквівлент інвестицій в умовах невизначеності.
Ці чотири аксіоми можуть використовуватися для побудови функції корисності. Ця функція може бути використана як основа моделі відношення інвесторів до ризику. Інвестори приймають рішення для того, щоб максимізувати власний очікуваний індекс корисності.
Нижче подано приклад, котрий показує процес, через який можна одержати функцію корисності інвестора.
Допустимо, що ми маємо інформацію про те, що якийсь індивідуум збирається зробити вкладення в певний інвестиційний проект. Необхідно вияснити, скільки максимально він може заплатити для того, щоб брати участь в цьому проекті. Існують тільки два результати цього проекту: одержати $5000 (+$5000) доходу або втратити $2000 (-$2000).
Для побудови функції корисності використаємо індекс корисності. Він повністю довільний, але для зручності ми позначимо одиницею індекс корисності для доходу +$5000 і нулем для доходу -$2000:
| Дохід | Індекс функції корисності |
| +$5000 | |
| -$2000 |
Це можна записати й по-іншому:
U(+$5000) = 1 U(-$2000) = 0
Якщо ймовірність доходу +$5000 рівна p, доходу — $2000 рівна (1 — p), тоді очікувана корисність проекту складатиме: р´U(+$5000) + (1-p) ´ U (-$2000). Так як U(+$5000) = 1, а U(-$2000) = 0, то очікувана корисність буде: р´1 + (1-р)´0 = р.
З аксіоми № 4 витікає, що з ризикованим доходом інвестор може порівняти еквівалентну безризикову альтернативу (Б–А). Вона представляє максимальну суму, що інвестор міг би заплатити за проект, який має ризик. У цьому випадку корисність безризикового еквівалента обчислюватиметься так:
U(Б-А) = р´U(+$5000) + (1-p) U´(-$2000)
U(Б-А) = р´1 + (1-р) ´0 = р
Тепер ми готові до побудови функції корисності для певного інвестора. Однак, необхідно підкреслити, що ця функція буде побудована для гіпотетичного інвестора. Різні інвестори будуть мати різні функції корисності, так як ці функції базуються на індивідуальному відношенні до ризику кожного інвестора.
Для побудови функції корисності певного інвестора ми можемо використати метод опитування, за допомогою якого необхідно з’ясувати, яку максимальну ціну готовий заплатити інвестор, щоб почати проект. Якщо, наприклад, ми говоримо йому, що ймовірність доходу проекту $5000 рівна 0,80 і ймовірність доходу — $2000 рівна 0,20, тоді інвестор може сказати, що він буде платити максимум $2000. Цей проект з безризиковою альтернативою і його індекс корисності обчислюється так:
U(Б-А) = р´U(+$5000) + (1-p) U´(-$2000)
U(Б-А) = 0.80´1 + 0.20´0 = 0.80
Потім ми можемо сказати, що ймовірність доходу +$5000 рівна 0.40 і тоді інвестор може виділити для участі в проекті безризиковий еквівалент
-$500. Індекс корисності в цьому випадку буде:
U(-$500) = 0.40´1 + 0.60´0 = 0.40
Ця процедура може продовжуватися багаторазово для більшої кількості різних ймовірностей. За її допомогою ми можемо скласти графік функції корисності цього інвестора. Подібний графік зображено на рис. 5-6.
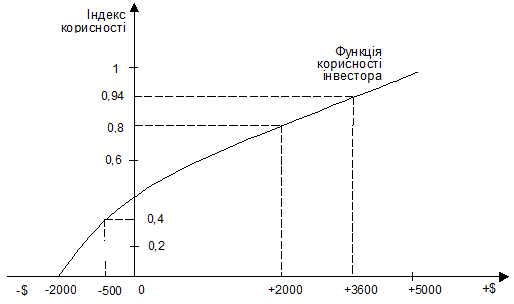
Рис. 5-6. Функція корисності
Детальніший аналіз функції корисності дозволяє одержати цю функцію в загальному вигляді, котрий описує відношення до ризику тих інвесторів, чия поведінка відповідає чотирьом поданим вище аксіомам.
Очікувана корисність доходу r від активу обчислюється рівнянням:
| E[U(r)] = f + bE(r) — cs2 + cE(r)2 | (5.4) |
де a, b, c — константи, що відображають індивідуальне відношення інвестора до ризику, а E(r) та s2 — очікування і дисперсія доходу відповідно
(s2 = E(r2) — E(r)2).
Модель оптимального портфеля інвестицій Марковіца
Теорія формування портфеля інвестицій, яка розглядається, передбачає, що інвестори заперечують ризик. Це значить, що вони намагаються одержати портфель з найменшим ризиком і за додатковий ризик вони хочуть одержати компенсацію додатковими доходами.
Модель Марковіца передбачає, що інвестор робить вибір серед безлічі можливих портфелів інвестицій на підставі лише двох факторів: середнього або очікуваного доходу (E(rp)) і ризику, виміряного через дисперсії (sp2) або стандартне відхилення (sp = s2p).
Якщо ми складемо портфель з двох активів А і B, то
E(rp) = x E(rA) + (1-x) E(rB)
sp2 = x2sA2 + (1 – x)2sB2 + 2x(1-x) sAB,
де х — частка активу А в портфелі, а sAB — коваріація доходів активів А і B. Вона визначається за формулою sAB = (1/n)S(rAi – E(rA))(rBi – E(rB)), де rAi і rВi — доходи від активів А і В за і-ий період часу (всього n періодів).
sAB = rАВsАsВ, де — коефіцієнт кореляції. Дисперсію портфеля можна подати також і через коефіцієнт кореляції rАВ = sAB /sАsВ, тоді:
sp2 = x2sA2 + (1 – x)2sB2 + 2x(1-x) rАВsАsВ.
Фундаментальним висновком теорії Марковіца є те, що диверсифікація (вкладення коштів не в один актив, а в різні) зменшує ризик портфеля, навіть якщо додані до портфеля активи мають більшу дисперсію (високий ризик). Розглянемо це на прикладі (рис. 5.7). Доходи з шести активів за 20 періодів були представлені через генератор випадкових чисел. Всі активи незалежні один від одного і зібрані у два інвестиційні портфелі А і B. Перший складається лише з одного першого активу (штрих-лінія). Портфель B (суцільна лінія) складається з рівних частин інших п’яти активів. Як бачимо на рисунку, дисперсія (відхилення) не диверсифікованого портфеля А вдвічі більша, ніж диверсифікованого портфеля B. Доходи портфеля B стабільніші (менш ризиковані) тому, що незалежні зміни різних активів у більшості компенсують один одного за рахунок стрибків у протилежних напрямках. Отже, диверсифікація зменшує ризик там, де доходи активів змінюються незалежно.
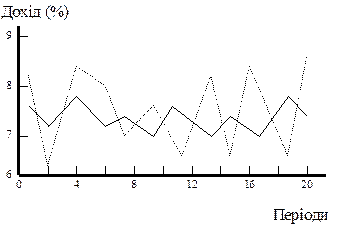
Рис. 5-7. Диверсифікація і ризик інвестиційних портфелів
Систематичний ризик
На жаль, у реальному світі неможливо так легко диверсифікувати ризик. Не існує дуже великої кількості активів, доходи з яких рухаються так незалежно, як у штучному прикладі. На противагу цьому доходи активів рухаються разом весь час через те, що на них діють одні й ті самі фактори. Фіскальна й монетарна політика, наприклад, штовхає майже всі доходи з активів в одному й тому ж напрямку. Глобалізація фінансових ринків збільшує швидкість реакції активів у всьому світі на зміну ситуацій у світових центрах фінансових ринків (Лондон, Нью-Йорк і Токіо).
Ризик від зміни доходу активу, яка відбувається в тому напрямку, що й зміна доходів інших активів, називається систематичним ризиком активу. Це призводить до систематичного ризику портфеля активів. Ризик від зміни доходу активу, яка відбувається цілком незалежно від доходів інших активів, називається несистематичним ризиком. Це спричинює несистематичний ризик портфеля активів.
Тільки систематичний ризик активу вносить значний вклад в ризик портфеля. Несистематичний ризик активу може бути усунутий за рахунок диверсифікації портфеля.
Розглянемо питання формування оптимального портфеля інвестицій. На рис. 5.8 точками показано можливу кількість портфелів для певного ринку. З кожним портфелем порівнюють його стандартне відхилення й дохідність, і за цими параметрами вони відрізняються один від одного.

Рис. 5-8. Формування оптимального портфеля інвестицій
Розглянемо портфелі А і B. Вони знаходяться на одній вертикальній лінії. Це означає, що дані два портфелі мають однакове стандартне відхилення доходів і значить однаковий ризик. Але портфель А знаходиться вище за B, тобто пропонує більший дохід. Тепер розглянемо портфелі А і С. Обидва пропонують однаковий дохід, але портфель С більше ризикований. Портфель А можна назвати ефективним: немає інших портфелів, котрі б давали великий дохід при меншому ризику або менший ризик при великому доході. Те саме можна сказати про точки Д і Е та про всі інші точки, які лежать на кривій ДАЕ, що називається ефективною границею численності портфелів. Саме на цій границі лежать портфелі, що найбільш привабливі для інвестора з погляду дохідності й ризику.
До цього часу ми мали справу з портфелями, котрі мають тільки активи з ризиком. Тепер розглянемо випадок, коли інвестор володіє комбінацією активів з ризиком і безризиковими активами (тобто активами, що мають нульову дисперсію доходів, це можуть бути, наприклад, державні облігації).
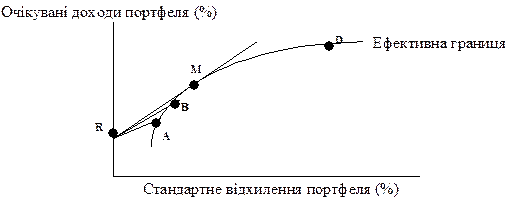
Рис. 5-9. Ефективна границя при комбінації ризикових і безризикових активів
Звернемося до рис. 5.9. На ньому бачимо три ризикових портфелі А, B і М, котрі об’єднані з безризиковим активом і лежать на ефективній границі. Портфель R складається тільки з безризикового активу. Лінія RA представляє всі можливі комбінації безризикового активу й ризикового портфеля А. З будь-яким портфелем, що знаходиться на ефективній границі нижче А, можна порівняти портфель на лінії RA, котрий буде мати більший дохід з рівним ризиком. Те саме можна сказати й про портфелі на лінії RB та інших портфелях на лініях, що з’єднують R з ефективною границею до точки М. Лінія RM є дотичною до ефективної границі. Портфелі, що знаходяться на цій лінії, переважають над усіма портфелями точки М, тому що інвестору немає сенсу вибирати нижчестоячі портфелі з погляду дохідності й ризику. Отже, з уведенням безризикового активу, ми одержуємо нову ефективну границю. Ця границя буде проходити по лінії RM, а потім переходить в криву MD.
Ефективна границя RMD має портфелі, які є найбільш переважними для інвестора. Безпосередній вибір (тобто точка на RMD) інвестора залежить від його відношення до ризику. Чим ризикованіший інвестор, тим більше його вибір портфеля буде зсунутим праворуч вздовж ефективної границі. Ця точка визначається перетинанням ефективної границі з кривою, котра визначається функцією корисності інвестора.
Якщо всі інвестори володіють одночасно всією інформацією про активи ринку, то згідно з нашим попереднім допущенням, вони будуть вкладати кошти, крім безризикового активу, виключно в активи портфеля М. Отже, на ринку будуть знаходитися лише безризикові активи і активи портфеля М. Такий портфель називається ринковим, він складається з усіх активів ринку.
Якщо ми продовжимо пряму RM далі, то опинимося в ситуації, коли інвестор має можливість використати позикові кошти для додаткових інвестицій. Причому ці кошти він може одержати при відсотковій ставці рівній дохідності безризикових активів. Така пряма називається лінією ринку капіталів (CML — Capital Market Line). Вона зображена на рис. 5-10.
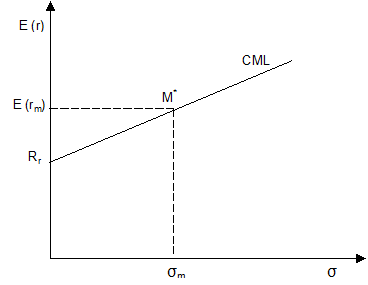
Рис. 5-10. Лінія CML
Очікуваний дохід від портфеля, що знаходиться на лінії CML, визначається рівнянням:
| E(rp) = xE(rm) + (1 — x)E(rf) | (5.5) |
де E(rm) і E(rf) — очікувані доходи від ринкового портфеля й безризикового активу відповідно. Так як стандартне відхилення безризикового портфеля (sf) нуль, то стандартне відхилення всього портфеля просте: sр = хsм, звідки х = sр/sм. Після підставлення й перегрупування, одержимо рівняння для очікуваного доходу портфеля, що лежить на CML:
E(rp) = rf + (E(rm) — rf) sр /sм
Очікуваний дохід від ефективного портфеля, що лежить на CML, можна розглядати як суму безризикового доходу й премії за ризик, котрий залежить від величини стандартного відхилення доходу портфеля.
Повернемося до поняття систематичного й несистематичного ризику. На рис. 5.11 подано різні види ризиків при збільшенні кількості активів у портфелі.

Рис. 5-11. Систематичний і несистематичний ризики
Як видно з рис. 5-11, при певній кількості активів у портфелі несистематичний ризик майже повністю усувається.
Ринковий портфель складається з усіх доступних активів, тому він не має несистематичного ризику, в ньому присутній лише систематичний або ринковий ризик. У цій ситуації активи будуть оцінені тільки відповідно з їх ринковим ризиком. Тому стандартне відхилення активу, котре відображає як систематичний, так і несистематичний ризики, більше не буде коректною мірою ризику. Такою мірою становиться коваріація активу з ринком. Ця міра ризику називається бета і звичайно позначається символом b.
Модель ціноутворення капіталних активів (CAPM — Capital Asset Pricing Model) була розроблена незалежно трьома економістами — Шарпом, Моссіним і Літнером. Вираз рівняння САРМ або лінії ринку активу звичайно записується так:
| E(ri) = rf + bi(E(rm) — rf), | (5.6) |
де очікуваний дохід від i–го активу з ризиком і bi дорівнює sim /sm2 або rimsi /sm.
Для виведення САРМ і коректного аналізу ринку, необхідно ввести деякі вимоги до ринку капіталів:
· інвестори оцінюють активи на підставі очікуваного доходу й стандартного відхилення (або варіації). З однаковим стандартним відхиленням інвестори віддають перевагу активу з більшим доходом;
· всі інвестори мають однаковий одноперіодний горизонт планування (гомогенні очікування);
· всі інвестори погоджуються з даною ймовірністю розподілу відсотка доходів;
· інвестиційні можливості однакові для всіх інвесторів, хоча вони можуть мати різні ресурси;
· передбачається, що не існує податків і плати за трансакції, всі активи можуть безмежно ділитися і ринок має досконалу конкуренцію;
· інвестори можуть брати кредит і кредитувати без обмежень з відсотком, що рівняється безризиковому доходу;
· всі фірми прийняли фінансові рішення і ніяких нових рішень не буде зроблено протягом розглядуваного періоду.
Звичайно, такі допущення не є реалістичними. Але як показало подальше вивчення і розвиток цієї моделі, вона досить добре працює в реальному ринку. Крім того, існують численні розширення цієї моделі, що дозволяють досягнути точнішого опису поведінки ринку. Нижче буде подано висновок САРМ.
Візьмемо будь-який актив і з E(ri) і si в точці В на рис. 5.12 та розглянемо комбінацію, яка є результатом інвестування частини хi коштів в актив і (1 – хi) в ринковий портфель М*.
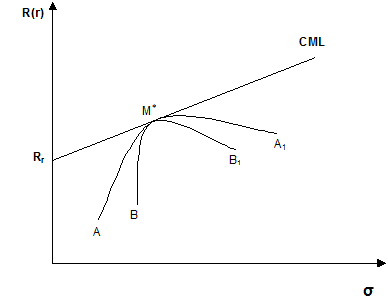
Рис. 5-12. Вивід САРМ
В точці В хi = 1; в точці М* утримується ринковий портфель хi = 0, але деяка кількість і буде в ринковому портфелі. В точці В1 немає активу і, тобто його було продано до цієї точки.
Очікуваний дохід і дисперсія доходів портфелів, що лежать вздовж ВМ*В1 мають вигляд:
(1) E(rp) = xiE(ri) + (1 — xi)E(rm)
(2) sp2 = xi2si2 + (1 — xi)2sm2 + 2xi (1-xi) sim
Як бачимо, СML і ВМ*В1 є дотичними до кривої АМ*А1. Тому нахил CML повинен рівнятися нахилу ВМ*В1 в М*. Ми знаємо, що нахил CML рівняється (E(rm) – rf) /sм. Потрібно знайти лише нахил ВМ*В1 до М*. Нахил ВМ*В1 є похідним dE(rp)/dsp. За ланцюговим правилом диференціювання:
dE(rp)/dsp = (dE(rp)/dxi) / ( dsp/dxi)
З рівняння (1):
(3) dE(rp)/dxi = E(ri) — E(rm)
З рівняння (2):
dsp/dxi = [xi (si2 + sm2 – 2sim) +sim – sm2]/ sp.
При М*, sp = sm і xi = 0, тому:
(4) (dsp/dxi)xi=0 = (sim – sm2)/ sm
dE(rp)/dsp = (рівняння 3)/(рівняння 4) = [(E(ri) – E(rm)) sm]/(sim – sm2 )
Так як в М* нахил CML рівняється ВМ*В1, то
[(E(ri) – E(rm)) sm]/(sim – sm2 ) = (E(rm) – rf) /sм
Спрощуючи, одержуємо:
E(ri) = rf + (E(rm) – rf) sim/ sm2 або E(ri) = rf + bi(E(rm) – rf).
Графічна лінія САРМ подана на рис. 5.13.
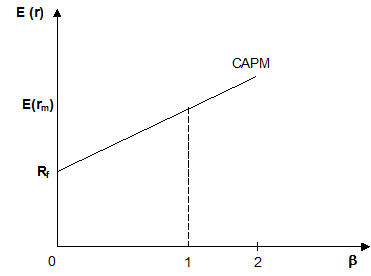
Рис. 5-13. Лінія САРМ
bі є показником чутливості доходів активу і доходів ринкового портфеля. Його публікують білшість великих фінансових періодичних видань для дуже багатьох акцій корпорацій, що представляють цілі галузі.
За bі можна робити висновок про поведінку доходів від активу і, залежно від зміни доходів, з ринкового портфеля. Отже, якщо:
· bі = 1, доходи від активу рухаються так само, як і доходи з ринкового портфеля;
· 0<bі<1, доходи від активу менші, за доходи з ринкового портфеля, коли ринок має позитивні доходи і більші за ринкові, якщо ринок дає негативні доходи;
· bі = 0, актив має такі ж доходи як і безризиковий актив;
· bі<0, доходи від активу й ринкового портфеля рухаються у протилежних напрямках.
Оцінення ефективності інвестиційного портфеля
Ефективність (якість) інвестиційного потфеля визначають як організації, котрі управляють портфелями, так і інвестори, що збираються вкласти свої кошти, наприклад, в акції інвестиційного фонду, якому належить портфель. Отже, методи, що будуть описані нижче можуть застосовуватися для оцінювання не тільки портфелів, але й компаній. Існує багато різних методів і критеріїв оцінювання портфелів. Ми зупинимося на основних. При цьому за приклад будемо оцінювати діяльність певного інвестиційного фонду як компанії, що управляє інвестиційним портфелем.
Розглянемо як приклад методи Трейнора, Шарпа і Дженсона, котрі базуються на моделі САРМ.
Метод Трейнора припускає, що розглядуваний портфель повністю диверсифікований або представляє частину повністю диверсифікованого портфеля, так що bр може бути мірою ризику цього портфеля. Із застосуванням методу обчислюється коефіцієнт Т:
T = 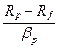 , ,
| (5.7) |
де Rp і Rf — дохідності розглядуваного портфеля й безризикового активу відповідно. Цей простий коефіцієнт дозволяє оцінити здатність управляючих інвестиційним фондом вибирати активи з вищим відсотком доходу, ніж в інших активів з таким самим ризиком.
Метод Шарпа відрізняється від методу Трейнора тим, що використовує стандартне відхилення дохідності портфеля sp (повний ризик) протягом розглядуваного періоду як знаменник при визначенні коефіцієнта S:
S = 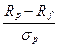
| (5.8) |
S дозволяє оцінювати не лише вибір найдохідніших активів, але й ефективність диверсифікації:
Метод Дженсона використовується, коли визначено коефіцієнт bp і для визначення ефективності вимагається порівняння дохідності розглядуваного портфеля з певним еталонним портфелем, що має такий же коефіцієнт b. Використовуючи САРМ, дохідність Rb еталонного портфеля обчислюється рівнянням: Rb = Rf + (Rm – Rf). Після цього визначають коефіцієнт J = Rp – Rb. Якщо J позитивне, то портфель і відповідний фонд переважають ринок.
Наведемо приклад використання останніх трьох методів оцінювання ефективності. Розглянемо три інвестиційні фонди — X, Y і Z, а також дохідність ринкового портфеля (наприклад індекс Stendard and Poor 500) за останні п’ять років. Дані подані в таблиці:
| Фонд | Щорічна дохідність (%) | b | Несистематичний ризик |
| X | 1.2 | ||
| Y | 1.8 | ||
| Z | 0.5 | ||
| S&P 500 |
За умови, що дохідність безризикового активу складає 10%, а стандартне відхилення S&P 500 було 25%, знаходимо:
Коефіцієнти Трейнора:
Tx =  = 0.067
= 0.067
Ty = 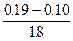 = 0.050
= 0.050
Tz = 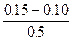 = 0.100
= 0.100
Коефіцієнти Шарпа:
Sx = 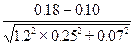 = 0.260
= 0.260
Sy = 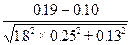 = 0.192
= 0.192
Sz = 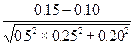 = 0.212
= 0.212
Коефіцієнти Дженсона:
Jx = 0.18 — (0.10 + 1.2(0.17 — 0.10)) = -0.004
Jy = 0.19 — (0.10 + 1.8(0.17 — 0.10)) = -0.036
Jz = 0.15 — (0.10 + 0.5(0.17 — 0.10)) = +0.015
Тепер можна ранжувати фонди за трьома коефіцієнтами:
| Коефіцієнт | Фонд X | Фонд Y | Фонд Z |
| Трейнора | |||
| Шарпа | |||
| Дженсона |
Якщо взяти середню оцінку, то фонд Z є ефективнішим за інші.
Модель середньозваженої вартості капіталу
Фінансові та інвестиційні рішення компанії тісно пов’язані між собою. Від того як буде фінансуватися проект, тобто, від того, яким буде співвідношення позикових і власних коштів, буде залежати рішення про участь або неучасть компанії в проекті.
Якщо VE і VB — поточна повна вартість акцій та облігацій випущених компанією, а Dt і It — дивіденди, що виплачуються компанією своїм акціонерам, і відсоткові платежі з облігацій або кредитів у проміжок часу t, то середньозважена вартість капіталу К0 обчислюється рівнянням [210]:
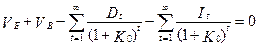 |
| (5.9) |
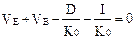
Так як у загальному вигляді при t>2 розв’язок цього рівняння явно не можна знайти (при його розв’язуванні необхідно використати методи обчислювальної математики), то зробимо реальне допущення, що компанія має безвикупні облігації та постійні дивіденди. Тоді К0 знаходимо наступним чином.
Помноживши на К0 і перегруповуючи одержимо:
VEК0+ VBК0 — D — I = 0
К0 (VE + VB) = D + I
К0 = (D + I)/(VE + VB)
З іншого боку, VE = D/KE, тоді D = VE і відповідно I = VBKD, підставляючи ці вирази у рівняння для К0, одержимо:
К0 = KEVE/(VE + VB) + KDVB/(VE + VB)
К0 використовується як коефіцієнт дисконтування при аналізі сучасної вартості потоку платежів проекту.
Застосування цього підходу ми покажемо пізніше під час розгляду моделі, що враховує податки.
Модель оптимальної структури капіталу
Якщо Y — повний щорічний грошовий потік компанії, тоді Y = VEKE + VBKD. Допустимо, що весь Y було виплачено дивідендами і платежами з облігацій, тоді повна ринкова вартість компанії обчислюється так:
| V0 = Y/K0 або Y = VEKE + VBKD, | (5.10) |
так як KE = D/VE = (Y – VBKD)/VE, то взявши з цього виразу Y і підставивши його в попереднє рівняння, одержимо:
KE = K0 + (K0 – KD) VB/VE
Це рівняння визначає так звану модель М-М (за першими літерами американських економістів Модігліані й Міллера) без урахування податків. Відношення VB/VE визначає структуру капіталу або ліверідж.
На рис. 5.14 видно як змінюються KE, K0, KD і V0 при зміні ліверіджу.
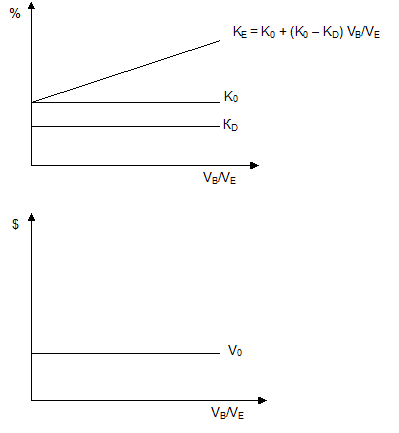
Рис. 5-14. Залежність KD, K0, KВ, V0 від ліверіджу в моделі М-М
без урахування податків
Так як компанії з активами, що мають однаковий ступінь ризику (з однаковими коефіцієнтами b для активів), мають однакову середньозважену вартість капіталу, попередній вираз можна записати так:
KEg = KEug + (KEug – KD) VB/VE,
де KEg — вартість власного капіталу компанії, що має не нульовий ліверідж, а KEug — вартість капіталу компанії без ліверіджу, але з таким же ризиком, як і компанії з ліверіджом. Символами будемо користуватися і далі для обчислення ліверіджу.
Для розгляду моделі з урахуванням податків будемо використовувати спрощену податкову систему з єдиним корпоративним податком, що платиться з прибутку корпорації після сплати нею зобов'язань з облігацій або кредитів. Тоді модель М-М з урахуванням податків записується так:
KEg = KEug + (KEug – KD)VB(1 – Т)/VE
K0 = KEug (1 – VBT/V0)
V0 = VEug + VBT,
де Т — корпоративний податок.
На рис. 5.15 видно як KE, K0, KD і V0 змінюються залежно від ліверіджу з урахуванням податків.

Рис. 5-15. Залежність КВg, K0, KD, B0g від ліверіджу в моделі М-М з урахуванням податків
Використання моделі М-М для аналізу інвестиційного проекту розглянемо на прикладі.
Нехай якась компанія АВС має власний капітал $12 млн., вартість її акціонерного капіталу 18%, АВС має намір зробити інвестиції вартістю $3 млн. для розширення свого виробництва. Даний інвестиційний проект має NPV, що рівняється +$1 млн.
Для фінансування проекту компанія має намір випустити $3 млн. безвикупних облігацій з 10% платежом. Корпоративний податок — 35%. Необхідно проаналізувати, який вплив матиме проект і його фінансування на:
1. Повну ринкову вартість компанії, VO;
2. Добробут акціонерів;
3. Середньозважену вартість капіталу;
4. Вартість акціонерного капіталу.
Використовуючи модель М-М, знаходимо:
1. До проекту: V0 = VE = VEug = $12 млн.
Нове значення V0, одержане в результаті зміни капітальної структури, обчислюється рівнянням:
V0 = VEug + VBT
V0 = $12м. + $3м.´ 0.33 = $12.99
Ми не повинні забувати, що в цьому прикладі $3 млн. додаткових активів додано в компанію і плюс NPV проекту. Отже, нова ринкова вартість компанії, після обліку не тільки змін у капітальній структурі, але й нових активів, буде:
V0 = $12.99 + $3м.+ $1м. = $16.99 млн.
2. Так як V0 = VE + VB, то VE = V0 — VB, отже:
VE = $16.99 – $3м. = $13.99 млн.
Тому добробут акціонерів, представлений повною ринковою вартістю акціонерного капіталу, підвищився на $1.99 млн.
3. Так як до проекту K0 = KE = KEug = 18%, то нова середньозважена вартість капіталу складатиме:
K0 = KEug (1 – VBT/V0)
K0 = 18% ´ (1 – ($3м.0.33)/$16.99) = 16.95%
Таким чином, збільшення ліверіджу компанії АВС викликало падіння середньозваженої вартості капіталу від 18% до 16.95%.
4. Використовуємо рівняння М-М:
KE Читайте також: Переглядів: 1056 Не знайшли потрібну інформацію? Скористайтесь пошуком google:
<== попередня сторінка
|
наступна сторінка ==>
Модель оцінювання терміну окупності | А.Г. ОЛЕКСИН, М.Г. МАРИЧ
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |