
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Поняття визначника. Визначники другого і третього порядків
Розв’язування багатьох економічних задач зводиться до розв’язування систем лінійних алгебраїчних рівнянь. В основі де-яких методів розв’язування таких систем використовуються вирази, які називаються визначниками ( або детермінантами).
Розглянемо квадратну таблицю з n2 чисел, розміщених в n - горизонтальних і n -вертикальних рядах. За спеціальними правила-ми знаходиться число, яке називають визначником n -го порядку і позначають буквою " " грецького алфавіту:
| a11 | a12 | ... | a1n | ||
| = | a21 | a22 | ... | a2n | . |
| .............................. | |||||
| an1 | an2 | ... | ann |
Числа aij( i = 1,2,...,n, j = 1,2,...,n ) - називають елементами
визначника. Перший індекс вказує номер рядка, а другий – номер стовпця, на перетині яких знаходиться елемент. Елементи, в яких обидва індекси однакові (тобто елементи a11,a22,...,ann ) утворюють
головну діагональвизначника.Інша діагональ називаєтьсянеголо-вною(допоміжною).Порядоквизначника визначає кількість йогорядків (або стовпців).
При обчисленні визначників n -го порядку одержуємо число, яке дорівнює алгебраїчній сумі всіх можливих добутків його еле-ментів, взятих по одному з кожного з n рядків і кожного із n стов-пців. При цьому половина доданків мають свої знаки, а інша - про-тилежні.
Покажемо, як обчислюються визначники другого і третього порядків. Для уточнення поняття “визначник” розглянемо два лінійних рівняння з двома невідомими з буквеними коефіцієнтами:
a11 x1 + a12 x2 = b1 , a21 x1 + a22 x2 = b2 .
Для розв’язування цих рівнянь ми повинні помножити їх на
відповідні коефіцієнти, при яких виключається одне з невідомих:
| a11 x1 + a12 x2 | = b1 , | a22 , − a21 | ||
| a21 x1 + a22 x2 | = b2 . | − a12 ,a11 |
В залежності від використаної пари множників ( по вертикалі) виключаємо або x1 або x2 і отримаємо такі рівняння:
( a11a22 − a12a21 )x1 = b1a22 − b2a12 ,
( a11a22 − a12a21 )x2 = b2a11 − b1a21 .
Звідси
| x1 = | b1a22 − b2a12 | , x2 = | b2a11 − b1a21 | . | ||
| a11a22 − a12a21 | a11a22 − a12a21 | |||||
| Ці вирази мають зміст тільки при умові, якщо знаменник не | ||||||
| дорівнює нулю. | ||||||
| Якщо, a11a22 − a12a21 = 0 , то | система рівнянь або немає | |||||
розв’язку , або має нескінченну множину розв’язків. Коефіцієнти при невідомих утворюють вирази, які називаються визначниками.
Розглядаючи ці коефіцієнти, ми бачимо, що вони однакові при обох невідомих; складаються з двох добутків,кожний з яких вклю-чає два елементи.
Визначники другого порядку символічно позначаються так:
a11 a12 .

 a21 a22
a21 a22
Визначником другого порядкуназивається число,яке дорів-
нює різниці добутків елементів головної і допоміжної діагоналей,
| тобто | a11 | a12 | = a11a22 − a12a21 . | |||||||||||||||
| a21 | a22 | • | • | |||||||||||||||
| Це ілюструється схемою: | a11 | a12 | = | a11 | − | a12 | . | |||||||||||
| a21 | a22 | • | a22 | a21 | • | − 3 | ||||||||||||
| Приклад 1.Обчислити визначник другого порядку: | . | |||||||||||||||||
Розв’язування. За попередньою формулою знаходимо:
1 − 3 = 1 ⋅ 6 − ( −3 )⋅7 = 6 + 21 = 27.

 76
76
Визначником третього порядкуназивається число,яке зна-
ходиться за формулою
| a11 | a12 | a13 | |
| a21 | a22 | a23 | = a11a22a33 + a12a23a31 + a21a32a13 − |
| a31 | a32 | a33 | − a13a22a31 − a12a21a33 − a23a32a11 . |
Знаки, які стоять перед кожним із доданків, слід вибирати з такої схеми:
| a11 | a12 | a13 | a11 • | • | • | a12 • | • | • | a13 | ||||||||||||||||||||||||||||||||||||
| a21 | a22 | a23 | = | • | a22 | • | + | • | • | a23 | + | a21 | • | • | − | ||||||||||||||||||||||||||||||
| a31 | a32 | a33 | • | • | a33 | a31 | • | • | • | a32 | • | ||||||||||||||||||||||||||||||||||
   
| • | • | a13 | • | a12 • | a11 • | • | ||||||||||||||||||||||||||||||||||||||
| − | • | a22 | • | − | a21 | • | • | − | • | • | a23 | . | |||||||||||||||||||||||||||||||||
| a31 | • | • | • | • | a33 | • | a32 | • | |||||||||||||||||||||||||||||||||||||

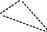
Це правило обчислення визначників 3-го порядку називається правилом трикутників.Тут доданки із знаком“+”є добуткамиелементів, які стоять на головній діагоналі визначника a11,a22,a33 і
добутки елементів, які стоять у вершинах трикутників з основами паралельними головній діагоналі a12,a23,a31 і a13,a21,a32 . Із знаком
“-” беруться доданки, які є добутками елементів неголовної діагона-лі a13,a22,a31 і добутки елементів вершин трикутників із основами,
паралельними цій діагоналі визначника: a12,a21,a33 і a11,a23,a32 .
| Приклад 2.Обчислити визначник= | − 2 | ||||||
| − 3 | . | ||||||
| − 4 |
Розв’язування. Користуючись правилом трикутників,
| − 2 | ||||||
| одержимо | − 3 | = 3 ⋅ 4 ⋅ ( −4 ) + ( −2 )( −3 )⋅ 5 + 1 ⋅ 2 ⋅ 0 − 0 ⋅ 4 ⋅ 5 − | ||||
| − 4 |
− ( −2 )⋅ 1 ⋅ ( −4 ) − ( −3 )⋅ 2 ⋅ 3 =−48 + 30 + 0 − 0 − 8 + 18 =−8.
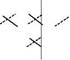
Правило трикутників легко запам’ятати, якщо дописати поряд з визначником перший, а потім другий його стовпці. Добутки еле-ментів, які знаходяться на діагоналях, відмічених на схемі суціль-
ними лініями, беруться із знаком “+”, a добутки елементів, які зна-ходяться на діагоналях, позначених на схемі пунктиром, із знаком “-”. Алгебраїчна сума цих шести добутків і дає значення визначника
a11 a12 a13 a11 a12


 a21 a22 a23 a21 a22 .
a21 a22 a23 a21 a22 .
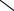
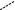
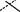 a31 a32 a33 a31 a32
a31 a32 a33 a31 a32
Такий спосіб обчислення визначника третього порядку нази-
вається правилом Саррюса.
Обчислимо попередній визначник 3-го порядку за правилом Саррюса.
| − 2 | − 2 | = 3 ⋅ 4 ⋅ ( −4 ) + ( −2 )( −3 )⋅ 5 + 0 ⋅ 1 ⋅ 2 − 0 ⋅ 4 ⋅ 5 − | ||||||
| − 3 | ||||||||
| − 4 |


− 3 ⋅ ( −3 )⋅ 2 − ( −2 )⋅ 1 ⋅ ( −4 ) =−48 + 30 + 0 − 0 + 18 − 8 =−8.
При обчисленні визначників використовують їх властивості, які розглядаються в наступному параграфі.
Зауваження. Визначником першого порядку є число,яке дорі-внює цьому елементу, тобто а11 = а11. Тому не слід плутати позна-чення визначника з модулем самого числа.
Читайте також:
- II. Поняття соціального процесу.
- V. Поняття та ознаки (характеристики) злочинності
- А/. Поняття про судовий процес.
- Автоматизовані станції управління насосними станціями водопостачання першого, другого і третього підйомів
- Адміністративний проступок: поняття, ознаки, види.
- Адміністративні правовідносини: поняття, ознаки,
- Адміністративні провадження: поняття, класифікація, стадії
- Акти застосування юридичних норм: поняття, ознаки, види.
- Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
- АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ
- АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ
- Аудиторські докази: поняття та процедури отримання
| <== попередня сторінка | | | наступна сторінка ==> |
| Розділ 1. ЕЛЕМЕНТИ ЛІНІЙНОЇ АЛГЕБРИ | | | Властивості визначників |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |