
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ТЕОРЕМА 1. Довільна квадратична форма приводиться до канонічного вигляду.
Доведення. Нехай задана квадратична форма(2.44)з матри-
→ → →
цею (2.45) в базисі e1,e2,..., en.
Так як A симетрична матриця, то існує ортогональна матриця
| λ | 0 ... | |||||||||
| λ 2 | 0 ... | |||||||||
| B така,що C = B | − 1 | AB = | 0 | |||||||
| ... ... | ... ... | ... . | ||||||||
| 0 ... | ||||||||||
| λ n | ||||||||||
| Матриця B є матрицею переходу від базису | ||||||||||
| → | → | → | ||||||||
| до деякого базису | e 1 ,e2 ,..., e n , | (2.46) | ||||||||
| → | → | → | ||||||||
| e 1∗ | , е2 | ∗ | ,..., e n∗. | (2.47) |
Примітка. Дійсна квадратна матриця називається ортогональ-ною, якщо сума квадратів елементів кожного стовпчика дорівнює одиниці і сума добутків відповідних елементів із двох різних стовпчиків дорівнює нулю. Необхідна і достатня умова
ортогональності матриці В є умова ВT ⋅ B = Е.
→
Нехай X і Y є вектори- стовпчики із координат вектора x відповідно в базисах (2.46) і (2.47). Тоді X = BY і
X T AX = ( BY )T A( BY ) = Y T BT ABY = Y T B−1 ABY = Y T CY
або
| X T AX =λ 1 y12 +λ 2 y22 + ...+λ n yn2 . | (2.48) |
Примітка. При доведенні даної теореми використали транс-понування добутку матриць за формулою (СY )T = YT ⋅ CT.
Зауважимо, що в канонічній формі (2.48) λ 1,λ 2,...,λ n є влас-ними числами матриці A .
Приклад 2.Привести квадратичну форму2x12+4x1x2+5x22до
канонічного вигляду з допомогою ортогональної матриці і знайти її. Розв’язування. Матриця даної квадратичної форми має вигляд
| для знаходження влас- | ||||
| А = | . Запишемо систему типу (2.39) | |||
них чисел і власних векторів
| ( 2 − λ )x1 + 2 x2 = 0 , | |||||||||||
| (2.49) | |||||||||||
| 2 x1 + ( 5 − λ )x2 − 0. | |||||||||||
| Характеристичне рівняння даної системи має вигляд | |||||||||||
| A − λE | = | 2 − λ | = 0 або ( 2 − λ )( 5 − λ ) − 4 = 0. | ||||||||
| 5 − λ | |||||||||||
| Розв’язавши дане рівняння знаходимо λ 1 = 6 ,λ 2 = 1. | |||||||||||
| Значить канонічний | вигляд даної квадратичної форми є |
6 y12 + y22 .
Знайдемо ортогональну матрицю.
Стовпчиками ортогональної матриці, яка приводить квадрати-чну форму до канонічного вигляду є ортонормовані власні вектор-стовпчики матриці A.
Спочатку знайдемо нормований власний вектор-стовпчик ма-триці A з власним значенням λ 1 = 6.Для цього із системи (2.49) ма-
| ємо систему для знаходження координат вектора − 4 x1 + 2 x2 = 0 , | ||||||
| 2 x1 − x2 = 0. | ||||||
| Із даної системи знаходимо x2 = 2 x1 або u2 = 2u1 . | ||||||
| Значить при довільному u1 , відмінному | від | нуля, стовп- | ||||
| чик u1 є власним вектором-стовпчиком матриці | A, а стовпець | |||||
| 2u1 | ||||||
| є нормованим власним вектором-стовпчиком матриці A. (Тут | ||||||


| → | → | ||||||||||||||||||||||
| використано, що | = | a | .Аналогічно | знаходимо | вектор-стовпчик | ||||||||||||||||||
| a | |||||||||||||||||||||||
| → | |||||||||||||||||||||||
| a | |||||||||||||||||||||||
| матриці A з власним | |||||||||||||||||||||||
| значенням λ 2 = 1 , а саме із системи: | |||||||||||||||||||||||
| x1 + 2 x2 = 0 , | |||||||||||||||||||||||
| 2 x1 + 4 x2 = 0. | |||||||||||||||||||||||
| Знаходимо | x1 =−2 x2 або при довільному | s ,яке відмінне від | |||||||||||||||||||||
| нуля, | стовпчик | − 2s є | власним | вектором матриці | A.Стовпчик | ||||||||||||||||||
| s | |||||||||||||||||||||||
| − | |||||||||||||||||||||||
| 5 є нормованим власним вектором матриці | A.Значить шука- | ||||||||||||||||||||||
| − | |||||||||||||||||||||||
| на матриця має вигляд B = | . | ||||||||||||||||||||||
| Зауваження.Легко перевірити,що С = B | − 1 | ||||||||||||||||||||||
| AB = | для | ||||||||||||||||||||||
| 0 | 1 |

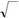
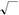
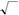
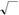
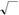 даного приклада 2.
даного приклада 2.
Розглянемо на прикладі ще один метод приведення квадрати-чної форми до канонічного вигляду.
Метод Лагранжа приведення квадратичної форми до каноніч-ного вигляду заключається в послідовному виділенні повних квад-ратів.
Приклад 3.Привести до канонічного вигляду квадратичну
форму L( x1, x2, x3) = x12 − 6 x1x2 + 4 x1x3 + 2 x2x3 + x32 методом Лаг-
ранжа. Спочатку виділимо повний квадрат при змінній x1 , коефіці-єнт при якій відмінний від нуля.
L =[x 12 − 2 x1 ( 3 x2 − 2 x3 ) + ( 3 x2 − 2 x3 )2 ]+ 2 x2 x3 + x32 −
− ( 3 x2 − 2 x3 )2 = ( x1 − 3 x2 + 2 x3 )2 + 2 x2 x3 − 9 x22 + 12 x2 x3 − 3 x33 == ( x1 − 3 x2 + 2 x3 )2 + 2 x2 x3 + x32 − 9 x22 + 12 x2 x3 − 4 x32 = ( x1 − 3 x2 +
| + 2 x3 | )2 − 9( x22 − | 2 ⋅7 | x2 x3 | + | x32 ) + ( | x32 − 3 x32 ) = | ||||||||||
| = ( x1 − 3 x2 + 2 x3 )2 − 9( x2 | − | x3 )2 + | x32 . | |||||||||||||
| І так, невироджене лінійне перетворення | ||||||||||||||||
| y1 = x 1 − 3 x2 + 2 x3 , y2 = x2 | − | x3 , y3 = x3 | ||||||||||||||
приводить дану канонічну форму до канонічного вигляду
L1 ( y1 , y2 , y3 ) = y12 − 9 y22 + 22 y32 .
 9
9
Канонічний вигляд квадратичної форми не є однозначним, так як одна й та ж квадратична форма може бути приведена до каноніч-ного вигляду багатьма способами. Однак одержані різними спосо-бами квадратичні форми мають ряд спільних властивостей.
Сформулюємо одну із цих властивостей, яка виражає закон інерції квадратичних форм, що заключається в наступному: всі ка-нонічні форми, до яких приводиться дана квадратична форма, ма-ють:
1) одне й те ж число нульових коефіцієнтів;
2) одне й те ж число додатніх коефіцієнів;
3) одне й те ж число від’ємних коефіцієнтів.
Означення1.Квадратична форма L( x1 , x2 ,..., xn ) назива-
ється додатньо визначеною, якщо для всіх дійсних значень x1 , x2 ,..., xn використовується нерівність L( x1 , x2 ,..., xn ) > 0 .
Означення2. Якщо L( x1 , x2 ,..., xn ) є додатньо визначеною формою, то квадратична форма L( x1 , x2 ,..., xn ) < 0 називається
Читайте також:
- II. Критерій найбільших лінійних деформацій
- III.4 Форматування тексту.
- IV. Виклад інформаційного матеріалу
- IV. Виклад інформаційного матеріалу
- IV. Критерій питомої потенціальної енергії деформації формозміни
- IV. Прийняття рішень у полі четвертої інформаційної ситуації
- R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
- Tема 4. Фації та формації в історико-геологічному аналізі
- V. Прийняття рішень у полі п’ятої інформаційної ситуації
- VI. Прийняття рішень у полі шостої інформаційної ситуації
- Абсолютизація формально-технічних пошуків у мистецтві ХХ ст.
- Автоматизована форма обліку
| <== попередня сторінка | | | наступна сторінка ==> |
| Квадратичні форми. | | | Від’ємно визначеною. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |