Точці цього проміжку.

Для встановлення проміжків, на яких графік функції

y = f ( x ) опуклий,а на яких вгнутий,вкажемо теорему,яка дає

достатні умови опуклості і вгнутості кривих на проміжку.

ТЕОРЕМА.Якщо на проміжку ( a ,b ) друга похідна функ-ції y=f ( x ) від’ємна, то її графік опуклий на цьому проміжку, якщо f '' ( x ) додатня на ( a ,b ) , то графік y=f ( x ) вгнутий.

Не приводячи строгого доведення, приведемо геометричні міркування, які пояснюють теорему.

Якщо скрізь на проміжку (a,b) f″(x)<0, то це означає, що f′(x), як функція для якої f″(x) є похідною, буде спадною. Отже, спадає на розглядуваному проміжку кутовий коефіцієнт дотичної tgα до кри-вої і спадає сам кут α, утворюваний дотичною з додатним напрямом осі Ox (мал12).

Очевидно крива на проміжку ( a ,b ) розташована під дотич-ною. Якщо f '' ( x ) > 0 , то крива буде угнутою.

Означення4. Точка, яка відокремлює опуклу частину непе-рервної кривої від вгнутої чи навпаки, називається точкою пере-гину.

	Необхідні умови існування точки перегину дає теорема.
	ТЕОРЕМА. Якщо x₀ - точка перегину неперервної функ-
ції	y = f ( x ) ,то друга похідна її	f '' ( x ) в цій точці
дорівнює нулю або не існує.				у
	Точки, в яких	f '' ( x )	дорівнює нулю

або не існує називають критичними точками
другого роду.
	Проте умови теореми не є достатніми.
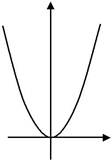
Так	для	функції	y = x ⁴	друга	похідна
y'' = 12 x ²	дорівнює нулю при	x = 0.	Проте
графік її вгнутий в цій точці (мал.14).		Мал.1 ^О	х

◙ Достатні умови існування точки перегину.

ТЕОРЕМА. Якщо друга похідна f '' ( x ) в точці x ₀ дорів-нює нулю і міняє знак при переході через цю точку, то точка з

абсцисою x₀	є точкою перегину кривої y=f ( x ) .
Доведення. Припустимо,що в точці М з абсцисою	x = x₀ ,
друга похідна	f '' ( x ) = 0 і при переході через неї зліва на право
змінює знак з мінуса на плюс. Тоді зліва від М крива	опукла
( f '' ( x ) < 0 ),	а справа крива вгнута ( f '' ( x ) > 0 ).Отже, в точці М

крива змінює опуклість на вгнутість, і тому точка М є точкою пере-гину.

Приклад.Знайти точки перегину і визначити проміжки

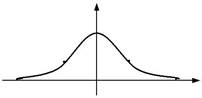
опуклості та вгнутості кривої y = e ⁻	x ²
		(крива Гаусса).
				−	x ²
Знаходимо похідні:	y' =− xe		,

	x ²	x ²				x ²
y'' =−e ⁻		₊ _x 2 _e ⁻	= ( x ²	− 1 )e ⁻
		2 _.

Прирівнюємо другу похідну до нуля і знаходимо критичні

−

x²

² = 0, x²

− 1 = 0 ,

=−1,

= 1.

точки другого роду: ( x² − 1 )e

Ці точки розбивають область визначення функції на проміж-

ки:

( −∞ ,−1 ),( −1,1 ),( 1,∞ )

(мал.15). Знаходимо знаки другої _Мал_{.1 -}

похідної в цих проміжках.

Отже, точки

x₁ =−1,

x₂ = 1

є точками

перегину.

На

проміжку ( −1,1 ) − крива опукла,

на проміжках ( −∞ ,−1 ) ∪ ( 1,∞ ) -

-1

крива вгнута (мал.16).

Мал.16

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Асимптоти графіка функції

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.01 сек.