Поверхні другого порядку

Найбільш вивчені поверхні в курсі аналітичної геометрії – по-

верхні другого порядку. В загальному	z
випадку рівняння такої поверхні має ви-

гляд.
a₁₁ x² + 2a₁₂ xy + a₂₂ y² + 2a₁₃ xz + 2a₂₃ yz + a₃₃ z² + 2a₁₄ x + 2a₂₄ y +
+ 2a₃₄ z + a₄₄ = 0.
Залежно від значень коефіцієнтів	O

Мал.3

a₁₁ ,a₁₂ ,a₂₂ ,...,a₄₄ одержують різні поверхні другого порядку.

Наприклад:

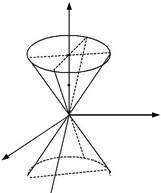
1)	x²	+	y²	−	z²	= 0
a²	b²	c²

- конус;

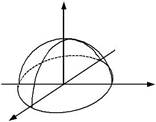
2) z = R² − x² − y²
- напівсфера;
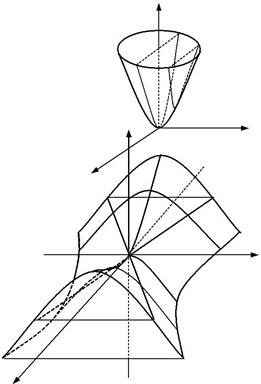
3) z =	_x2	+	_y2	-

a²	b²

еліптичний параболоїд;

-R

-R O R y

_R Мал.4 z

z ^O y

4) z =	x²	−	y²
2 p	2q

Мал.5

-гіперболічний параболоїд;

^x Мал.6

		x²		y²	z²	z
5)			+		+	= 1
	a²	b²	c²
	-трьохосний		с
		еліпсоїд.

							O	b
								y
						х		Мал.7

Для вивчення поверхонь в трьохвимірному просторі застосо-вується метод перерізів. Суть цього методу така: перерізаємо задану

поверхню площинами. x = C₁,	y = C_{2 ,}	z = C_3. В результаті отри-
муємо деякі криві, які характеризують поверхню.
Приклад 3.	z = x² + y² .	Нехай	z = C₁ ( C₁ ≥ 0 ). Отримаємо
рівняння x² + y²	= C₁ (рівняння кола).Покладемо y = C₂ , тоді

x² + C₂² = z -рівняння параболи в площині x0z ,яка зміщена на C₂² одиниць вверх по осі Oz . Покладемо x = C₃. Отримаємо рівняння

z = y² + C₃² .	Одержали рівняння параболи в площині y0z , яка
зміщена на C₃²	одиниць вверх по осі 0z. З цих досліджень випли-

ває, що графіком функції z = x² + y² є параболоїд обертання навко-ло осі 0z.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Поняття лінії та поверхні рівня	\|	Гіперповерхня рівня

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.