• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ІНФОРМАЦІЙНИЙ МОДУЛЬ 1

ОРТОГОНАЛЬНІ ПРОЕКЦІЇ ЕЛЕМЕНТАРНИХ ГЕОМЕТРИЧНИХ ПОБУДОВ

Точка

Теоретичною основою побудови технічних зображень є метод проекцій, який дає змогу діставати зображення просторових фігур на площині чи поверхні.

На рис.1.1 зображений приклад центрального проекціювання точок. Якщо взяти довільну точку S і сполучити її з іншими точками, то дістанемо в’язку прямих.

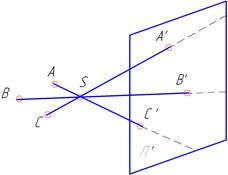S – центр проекціювання;

SA, SB, SC – проекціювальні проміні;

П΄ - площина проекцій;

A, B, C - точки;

A’, B’, C’ - проекції точок на П΄

Рисунок 1.1 – Просторова модель

системи центрального проекціювання

Якщо проекціювальні промені спрямувати у одному відповідному напрямку то дістанемо метод паралельного проекціювання (рис.1.2). Паралельне проекціювання може бути прямокутним (ортогональним) або косокутним.

АA’, BB’, CC’ - проекціювальні

промені;

П΄ - площина проекцій;

A, B, C - точки;

A’, B’, C’ - проекції точок на

площину П΄.

Рисунок 1.2 – Просторова модель

системи паралельного проекціювання

Залежно від положення площин проекцій та центрів проекціювання можна діставати різні проекційно-зображувальні системи. Найбільш поширеною є система прямокутних ортогональних проекцій або метод Монжа. За цим методом обираються площини, які перпендикулярні одна до одної (рис. 1.3, а).

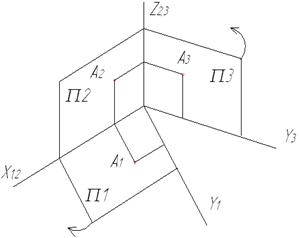
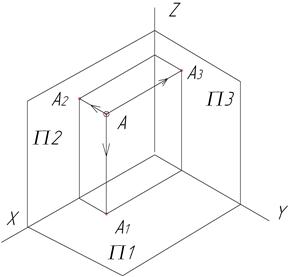
а) б)

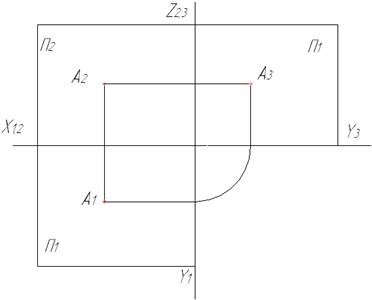
в)

Рисунок 1.3 – Перетворення просторової моделі системи площин проекцій в проекційне креслення: а) просторова модель; б) проміжний етап трансформації; в) проекційне креслення.

Якщо горизонтальну площину проекцій, обернути навколо осі Х проти часової стрілки на 90⁰, а профільну площину проекцій так саме навколо осі Z (рис. 1.3, б), то отримаємо плоске зображення проекцій точки А (рис.1.3, в). Таке зображення має назву проекційного креслення або епюра Монжа.

Горизонтальна і фронтальна площини проекцій поділяють простір на чотири октанти. На рисунках 1.4, 1.5 показані приклади проекцій точок, що розташовані в різних октантах.

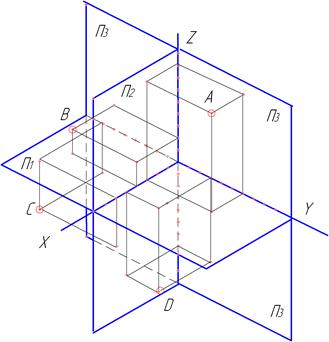
Рисунок 1.4 – Просторова модель системи площин проекцій з чотирьох октантів

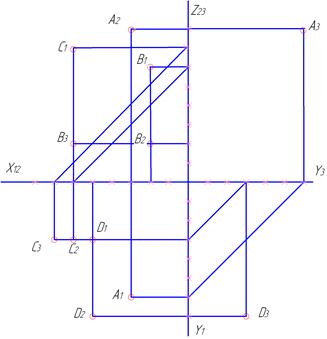
Рисунок 1.5 – Проекційне креслення точок розташованих в чотирьох октантах простору

Читайте також:

1. V міні – модуль
2. Виробничий і науково-технічний потенціал. Інформаційний потенціал
3. Високочастотні перетворювачі модульної структури
4. Галузі, на перетині яких розвивається інформаційний менеджмент
5. Друга модульна контрольна робота
6. Друга модульна контрольна робота
7. За конструктивними особливостями фритюр-ниці поділяють на секційно-модульні та ті, які входять до комплекту малогабаритного обладнання.
8. За кредитно-модульною системою
9. ЗАВДАННЯ МОДУЛЬНОЇ КОНТРОЛЬНОЇ РОБОТИ №1.
10. ЗАВДАННЯ ТА МЕТОДИЧНІ ВКАЗІВКИ ДО МОДУЛЬНОЇ КОНТРОЛЬНОЇ РОБОТИ № 1
11. ЗАВДАННЯ ТА МЕТОДИЧНІ ВКАЗІВКИ ДО МОДУЛЬНОЇ КОНТРОЛЬНОЇ РОБОТИ № 2
12. Заліковий МОДУЛЬ 1 . Економічна і соціальна географія світу

Переглядів: 743